Значение Cos φ
Cos φ в практической электротехнике имеет очень важное значение. Реальные нагрузки, типа электромоторов и трансформаторов, имеют большую индуктивную составляющую сопротивления, то есть, фактически, представляют собой цепи RL. Для таких цепей неизбежно существует сдвиг фаз, который приводит к тому, что полная мощность S значительно превышает активную мощность (P)
Для таких цепей неизбежно существует сдвиг фаз, который приводит к тому, что полная мощность S значительно превышает активную мощность (P).
Из формулы видно, что чем меньше Cos φ (Чем больше угол сдвига фаз), тем меньшую часть активная мощность составляет от полной мощности .
Только активная мощность является полезной, если источник затрачивает полную мощность, а от нагрузки мы можем получить только активную мощность, значит, Cos φ имеет смысл электротехнического КПД или коэффициента мощности.
В идеале источник должен отдавать такую мощность, которую будет потреблять нагрузка. Реальные устройства неизбежно содержат индуктивности (катушки, обмотки, и т.п.), значит, источник вынужден отдавать полную мощность, которая значительно больше, активной.
Проектирование устройств и электрических цепей должно иметь целью получить значение Cos φ как можно ближе к единице, то есть влияние индуктивности надо свести к минимуму. Плохие значения Cos φ приводят к большим неоправданным затратам электроэнергии.
RLC цепи: суть и работа
RLC цепь — это электрическая цепь, содержащая резистор (R), индуктивность (L) и емкость (C). Она используется для решения различных задач в электротехнике и электронике, таких как фильтрация сигналов, согласование импеданса и т.д.
Суть работы RLC цепи заключается в прохождении переменного тока через резистор, индуктивность и емкость. В зависимости от частоты сигнала, значение импеданса RLC цепи может меняться, что позволяет использовать ее для различных задач.
RLC цепь может работать в разных режимах, включая режим резонанса, когда значение импеданса цепи становится минимальным и достигает нуля. Это позволяет использовать RLC цепь для создания колебательных контуров и применять ее в схемах радиоприемников и передатчиков.
Для расчета параметров RLC цепи используются различные математические методы и формулы. Один из основных параметров RLC цепи — добротность (Q), которая показывает, насколько быстро энергия колебаний в RLC цепи затухает.
RLC цепь может быть представлена в виде графика зависимости импеданса от частоты, который называется АЧХ (амплитудно-частотной характеристикой). Также используется ФЧХ (фазово-частотная характеристика), которая показывает фазовый сдвиг между током и напряжением в RLC цепи в зависимости от частоты.
- RLC цепь — это электрическая цепь, состоящая из резистора (R), индуктивности (L) и емкости (C).
- Суть работы RLC цепи заключается в прохождении переменного тока через резистор, индуктивность и емкость.
- RLC цепь может работать в разных режимах, включая режим резонанса, когда значение импеданса цепи становится минимальным.
- Для расчета параметров RLC цепи используются различные математические методы.
- RLC цепь может быть представлена в виде графика зависимости импеданса от частоты, который называется АЧХ (амплитудно-частотной характеристикой).
Энергия электромагнитного поля
Опыт показывает, что в контуре из двух электроламп, соленоида и реостата при отключении источника тока еще некоторое время течет электрический ток, причем сила тока со временем уменьшается от некоторого начального значения до нуля.
Одновременно с током, как известно, исчезает и магнитное поле тока. Так как никаких других источников энергии, которые поддерживали бы электрический ток в контуре, нет, то остается предположить, что энергией обладает само магнитное поле. Найдем начальную энергию W магнитного поля, считая, что она расходуется на индуцирование э. д. с. и тока самоиндукции в контуре, когда магнитный поток убывает от некоторого начального значения до нуля.
Бесконечно малое изменение энергии поля равно элементарной работе тока в контуре:
Но э. д. с. самоиндукции , а сила тока i=dQ/dt. Отсюда
dW = — Lidi
Знак минус указывает, что энергия поля уменьшается. Интегрируя это выражение, находим
где
-потокосцепление;
— индуктивность или коэффициент пропорциональности между током и потокосцеплением;
— ток через катушку.
Потокосцеплением самоиндукции y цепи называется сумма произведений магнитных потоков, обусловленных только током в этой цепи, на число витков, с которыми они сцеплены.
Если все витки пронизываются одним и тем же магнитным потоком Ф, то потокосцепление равно произведению магнитного потока на число витков y=Фw, а w = nI, где I-длина соленоида, n — густота обмотки.
В СИ потокосцепление измеряется в веберах, индуктивность — в генри.
Генри — это индуктивность соленоида, в котором при силе тока 1 А создается магнитный поток 1 Вб.
Зависимость потокосцепления от тока может быть постоянной (линейная зависимость) или нелинейной.
При изменении тока изменяется потокосцепление и в катушке наводится ЭДС самоиндукции:
Знак минус показывает, что ЭДС противодействует изменению тока в цепи.
Напряжение и мощность индуктивности равны:
Мощность может быть как положительной (при намагничивании), так и отрицательной (при размагничивании).
При нарастании тока , направления тока и напряжения совпадают, в индуктивности запасается энергия магнитного поля.
При убывании тока , направления тока и напряжения не совпадают, энергия магнитного поля в индуктивности убывает, возвращается обратно к источнику.
Явление самоиндукции можно наблюдать на опыте, собрав цепь с источником постоянного тока и двумя параллельными ветвями (смотри рисунок выше). Одна ветвь состоит из электролампы Л1 и реостата R, другая — из такой же электролампы Л2 и соленоида. С помощью реостата в обеих ветвях устанавливают одинаковую силу постоянного тока. После включения рубильника видно, что лампа Л2 начинает светиться позже, чем лампа Л1. Это объясняется тем, что в соленоиде индуцируется э. д. с. самоиндукции, препятствующая некоторое время нарастанию силы тока. У разных соленоидов время нарастания силы тока оказывается различным, так как вокруг каждого из них создаются разной величины магнитные потоки, которые индуцируют различные э. д. с. самоиндукции.
Что такое резонанс напряжения?
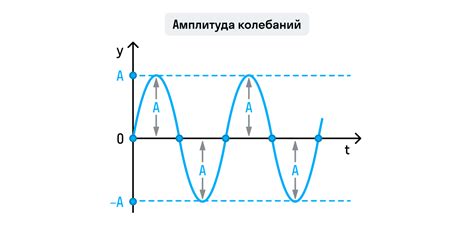
Резонанс напряжения – это явление, которое происходит в RLC цепи, когда реактивное сопротивление источника напряжения полностью компенсируются реактивными сопротивлениями индуктивности и емкости цепи.
При резонансе напряжения в цепи достигается наибольшее значение напряжения. В этом случае активное сопротивление цепи минимально, что позволяет передавать максимальную мощность от источника к нагрузке.
Чтобы достичь резонанса напряжения, необходимо настроить параметры RLC цепи — сопротивление, индуктивность и емкость. В зависимости от сочетания этих параметров источник может генерировать различные формы сигнала.
Резонанс напряжения имеет множество применений. Одно из главных применений — передача энергии через бесконтактные системы, такие как нагревательные катушки и беспроводные зарядные устройства для мобильных устройств.
Преимущества резонанса напряжения:
- Максимальная передача мощности
- Минимальные потери энергии
- Эффективное использование источника напряжения
- Удобство и гибкость в применении
Резонанс напряжения — важное явление в электротехнике и электронике, которое применяется в различных устройствах и системах для оптимизации передачи и использования электрической энергии
Принцип работы RLC цепи
Когда в RLC цепь подается переменный ток, индуктивность генерирует электромагнитное поле, а ёмкость — электрическое поле. Эти поля воздействуют друг на друга, приводя к образованию погонных токов, которые меняются во времени.
При особых значениях частоты переменного тока (резонансных частотах) в RLC цепи происходит максимальное совпадение фаз между током и напряжением, а сопротивление цепи минимально. В таком случае, цепь обладает наибольшей эффективностью и способна передавать большую мощность.
RLC цепи имеют широкий спектр применений, включая фильтрацию сигналов, регулирование частоты и амплитуды сигналов, стабилизацию напряжения и тока, а также использование в радиосвязи и электронных устройствах.
Влияние резонанса на электрические схемы
Резонанс напряжений — это явление, которое может возникнуть в электрической цепи, содержащей элементы с сопротивлением, индуктивностью и ёмкостью. В резонансном состоянии в схеме происходит усиление амплитуды напряжения на резисторе или конденсаторе, вызванное взаимодействием индуктивности и ёмкости.
Резонансное состояние может быть полезным и применяется в различных областях. Вот некоторые примеры:
- Резонанс используется в радио и телевизионных передатчиках для усиления сигнала на определённой частоте. При достижении резонанса настройка на нужную частоту становится более точной и эффективной.
- В медицинской технике резонанс применяется в MRI (магнитно-резонансной томографии), позволяя получить более детальные изображения внутренних органов и тканей.
- В автомобильной промышленности резонанс используется для оптимизации работы электронных систем, например, в системах зажигания и питания.
Существуют и нежелательные эффекты резонанса, которые могут негативно повлиять на работу электрических схем:
- Резонанс может вызвать перегрев элементов схемы, что может привести к их повреждению или выходу из строя.
- Ненужные резонансы могут приводить к искажению сигналов или помехам в схеме, что может снижать качество передачи или обработки данных.
- Резонанс может влиять на стабильность и надёжность функционирования электронных устройств.
Чтобы учесть эффекты резонанса при проектировании и эксплуатации электрических схем, необходимо проводить анализ и расчёты с учётом параметров элементов и условий работы схемы. Разработчики должны стремиться достичь оптимального баланса между получением желаемых эффектов резонанса и предотвращением нежелательных последствий.
Последовательная цепь RLC
Последовательная цепь RLC.
Цепь подвержена скачку напряжения
Если последовательная цепь RLC подвергается скачку напряжения , сеточный закон устанавливает соотношение:
E{\ Displaystyle E \,}
- Eзнак равнотыПРОТИВ+тыL+тырзнак равнотыПРОТИВ+Ldяdт+ртя{\ displaystyle E = u_ {C} + u_ {L} + u_ {R} = u_ {C} + L \, {\ frac {\ mathrm {d} i} {\ mathrm {d} t}} + R_ {t} \, i}
Путем введения характеристического соотношения конденсатора:
- яПРОТИВзнак равноязнак равноПРОТИВdтыПРОТИВdт{\ displaystyle i_ {C} = i = C \, {\ frac {\ mathrm {d} u_ {C}} {\ mathrm {d} t}}}
получаем дифференциальное уравнение второго порядка :
- LПРОТИВd2тыПРОТИВdт2+ртПРОТИВdтыПРОТИВdт+тыПРОТИВзнак равноE{\ Displaystyle L \, C \, {\ frac {\ mathrm {d} ^ {2} u_ {C}} {\ mathrm {d} t ^ {2}}} + R_ {t} \, C \, {\ frac {\ mathrm {d} u_ {C}} {\ mathrm {d} t}} + u_ {C} = E}
С участием:
- E электродвижущая сила генератора в вольтах ( В );
- у С напряжения на конденсаторе, в вольтах ( В );
- Л индуктивность катушки, в генри ( Н );
- я интенсивность электрического тока в цепи, в амперах ( );
- д электрический заряд конденсатора, в кулонах ( С );
- С электрической мощностью конденсатора, в фарадах ( F );
- R т в общем сопротивлении цепи, в Ом ( Ом );
- т на время в секундах ( ы )
В случае режима без потерь, то есть при , мы получаем решение в виде:
ртзнак равно{\ Displaystyle R_ {t} = 0 \,}
- тыпротивзнак равноE+Впотому что(2πтТ+φ){\ displaystyle u_ {c} = E + A \, \ cos \ left ({\ frac {2 \ pi t} {T_ {0}}} + \ varphi \ right)}
- Тзнак равно2πLПРОТИВ{\ displaystyle T_ {0} = 2 \ pi {\ sqrt {LC}}}
С участием:
- T период колебаний в секундах ;
- A и φ две константы, которые необходимо определить благодаря начальным условиям схемы.
Которые дают:
- жзнак равно12πLПРОТИВ{\ displaystyle f_ {0} = {\ frac {1} {2 \ pi {\ sqrt {LC}}}}}
Где собственная частота цепи в герцах ( Гц ).
ж{\ displaystyle f_ {0}}
Цепь подвержена синусоидальному напряжению
Сложное преобразование применяется к различным напряжениям позволяет записать закон сетки в виде:
- Uграмм_знак равноUПРОТИВ_+UL_+Uр_{\ displaystyle {\ underline {U_ {G}}} = {\ underline {U_ {C}}} + {\ underline {U_ {L}}} + {\ underline {U_ {R}}}}
либо путем введения комплексных сопротивлений :
- Uграмм_знак равно-jПРОТИВωя_+jLωя_+ртя_знак равнорт+jLПРОТИВω2-1ПРОТИВωя_{\ displaystyle {\ underline {U_ {G}}} = — {\ frac {j} {C \ omega}} {\ underline {I}} + jL \ omega {\ underline {I}} + R_ {t} {\ underline {I}} = {\ bigg } {\ underline {I} }}
Угловая частота по резонансной интенсивности такой цепи & omega определяется по формуле:
- ωзнак равно1LПРОТИВ{\ displaystyle \ omega _ {0} = {\ frac {1} {\ sqrt {LC}}}}
Для этой частоты указанное выше соотношение становится:
- Uграмм_знак равноUр_знак равнортя_{\ displaystyle {\ underline {U_ {G}}} = {\ underline {U_ {R}}} = R_ {t} {\ underline {I}}}
и у нас есть: UL_знак равно-UПРОТИВ_знак равноjртLПРОТИВUграмм_{\ displaystyle {\ underline {U_ {L}}} = — \, {\ underline {U_ {C}}} = {\ frac {j} {R_ {t}}} \, {\ sqrt {\ frac { L} {C}}} \; {\ underline {U_ {G}}}}
Условные обозначения источников электрической энергии и элементов цепей
| Условное обозначение | Элемент |
|
Идеальный источник ЭДС Е — электродвижущая сила, Е = const Ro = 0 — внутреннее сопротивление |
|
|
Идеальный источник тока I = const Rвн- внутреннее сопротивление источника тока, Rвн>>Rнаг |
|
|
Активное сопротивление R = const |
|
| Индуктивность L = const | |
| Емкость С = const |
К химическим источникам тока относят гальванические элементы и аккумуляторы. В них заряды переносятся в результате химических реакций. При этом в гальваническом элементе реагенты расходуются необратимо, а в аккумуляторе они могут восстанавливаться путем пропускания через аккумулятор электрического тока противоположного направления от других источников.
Источники электрической энергии относятся к группе активных элементов электротехнических устройств. Если Rо=0 и электродвижущая сила (ЭДС) Е=const, то источник называется идеальным. Аккумуляторная батарея по своим параметрам близка к идеальному источнику ЭДС.
К группе пассивных элементов относятся: активное сопротивление R, индуктивность L и емкость С.
В электротехнических устройствах одновременно протекают три энергетических процесса:
1 В активном сопротивлении в соответствии с законом Джоуля — Ленца происходит преобразование электрической энергии в тепло.
Мощность, по определению равна отношению работы к промежутку времени, за который эта работа совершается. Следовательно, мощность тока для участка цепи
p = A/t = ui
Полная мощность, вырабатываемая генератором, равна
где R- полное сопротивление замкнутой цепи, называемое омическим или активным;
Р, I — мощность и ток в цепи постоянного тока.
р, i, и — мгновенные значения активной мощности, тока и напряжения в цепи переменного тока,
g — активная проводимость или величина, обратная сопротивлению g=1/R измеряется в сименсах (См).
В соответствии с законом сохранения энергии работа есть мера изменения различных видов энергии. Так, в электродвигателе за счет работы тока возникает механическая энергия, протекают химические реакции и т. д. На резисторах происходит необратимое преобразование энергии электрического тока во внутреннюю энергию проводника.
Если в проводнике под действием тока не происходит химических реакций, то температура проводника должна измениться. Изменение внутренней энергии проводника (количество теплоты) Q равно работе А, которую совершает суммарное поле при перемещении зарядов:
Q = А = uit
Воспользовавшись законом Ома, получим два эквивалентных выражения:
Это и есть закон Джоуля — Ленца.
Если нужно сравнить два резистора по характеру тепловых процессов, происходящих в них, то нужно предварительно выяснить: протекает ли по ним одинаковый ток или они находятся под одинаковым напряжением?
Если по двум резисторам протекают одинаковые токи, то согласно формуле за одно и то же время больше возрастает внутренняя энергия резистора с большим сопротивлением. С таким случаем мы встречаемся, например, в цепи с последовательным соединением резисторов. Последнее обстоятельство следует учитывать при включении в сеть нагрузки (электроплиток, утюгов, электродвигателей и т. д.). Сопротивление подводящих проводов при этом должно быть значительно меньше, чем сопротивление нагрузки. При несоблюдении этого условия в проводах выделится большое количество теплоты, что может привести к их загоранию.
Если же оба резистора находятся под одинаковым напряжением, то согласно формуле быстрее будет нагреваться резистор с меньшим сопротивлением. Такой эффект, в частности, наблюдают при параллельном соединении резисторов.
Термин «сопротивление» применяется для условного обозначения элемента электрической цепи и для количественной оценки величины R.
Сопротивление измеряется в омах (Ом). 1 Ом — это сопротивление проводника, сила тока в котором равна 1 А, если на концах его поддерживается разность потенциалов 1 В:
1 Ом = 1 В/1 А
Электрическое сопротивление R материалов с изменением температуры меняется. Сопротивление металлических проводников линейно возрастает с температурой. У полупроводников и электролитов с увеличением температуры удельное сопротивление уменьшается, причем нелинейно.
Для сравнения проводников по степени зависимости их сопротивления от температуры t вводится величина a, называемая температурным коэффициентом сопротивления. Отсюда
Для практических расчетов в электрических цепях величину R можно принимать постоянной. В этом случае зависимость напряжения на сопротивлении R от силы тока (вольт-амперная характеристика) будет называться линейной. Электрические цепи, в которые включены постоянные по величине сопротивления, также будут линейными.
Формула
Поиск тока заряда конденсатора происходит по следующей формуле. Он измеряется в фарадах, что равно кулону или вольту.

Формула для нахождения заряда конденсатора
В общем, это элемент электрической сети, который накапливает и хранит внутри себя напряжение. Он доступен в различных типах и размерах, например, электролитический, керамический и танталовый. В основном он состоит из нескольких токопроводящих пластин с одним диэлектриком. Его емкость зависит от размера диэлектрика и наполнителя между пластинами. Заряжается электричеством. Зарядный ток конденсатора можно определить с помощью измерительных инструментов и формулы.
Широкое применение параллельной резонансной цепи RLC
Параллельные резонансные схемы RLC используются в области электронной техники, особенно в схемах настройки, проектировании фильтра и технологии сопоставления импеданса.Их гибкость и эффективность подходят для процессов и оптимизации электронного оборудования, что обеспечивает ясность и ясность передачи сигнала.точность.
В радиооборудовании функция настройки параллельной резонансной схемы RLC позволяет цепи представлять наименьшее значение импеданса на этой частоте, позволяя сигналам соответствующей частоты проходить в форме максимального тока, тем самым достигая эффективного приема сигнала и выбора.
В качестве фильтра параллельная резонансная цепь RLC может удалять ненужные компоненты частоты, установив резонансную частоту FO и коэффициент качества Q. Коэффициент качества Q, выраженный как , где это полоса пропускания цепи, отражает селективность схемы на резонансной частоте.Высокие цепи имеют узкую полосу пропускания и могут более точно отфильтровать конкретные частотные компоненты, в то время как схемы с низким Q подходят для широкополосной пропускной способности и обеспечивают более широкий диапазон возможностей фильтрации частоты.
С точки зрения сопоставления импедансов, корректировка и оптимизация параллельной резонансной схемы RLC может повысить общую эффективность и производительность цепи.Соответствие импеданса обеспечивает максимальную передачу энергии от источника к нагрузке, уменьшая отражения и потери энергии.Регулируя компоненты R, L и C в схеме, может быть достигнуто соответствие импеданса между источником и нагрузкой, а характеристики передачи схемы могут быть оптимизированы.Это может значительно повысить производительность системы и надежность в высокочастотной конструкции схемы, таких как радиочастотные системы передачи.
Благодаря тонкой настройке и оптимизации параметров схемы, инженеры могут разработать высокопроизводительные электронные системы, которые удовлетворяют конкретные потребности, будь то в связи с коммуникацией, вещанием или высокочастотной электроникой.
Цепь RC:
Цепи RC (резистор конденсатор цепь) будут состоять из конденсатора и резистор соединены последовательно или параллельно напряжения или источник тока. Эти типы схем также называются RC-фильтрами или RC- цепями, поскольку они чаще всего используются в приложениях фильтрации. RC-цепь может использоваться для создания некоторых грубых фильтров, таких как фильтры нижних и верхних частот и полосовые фильтры. Схема первого порядка RC будет состоять только из одного резистора и одного конденсатора, и мы будем анализировать то же самое в этом руководстве
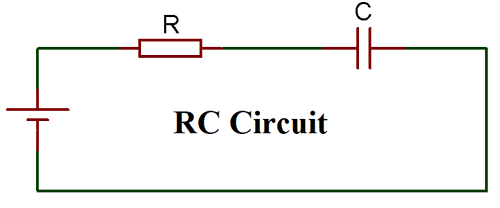
Чтобы понять RC-схему, давайте создадим базовую схему на Proteus и подключим нагрузку через осциллограф, чтобы проанализировать его поведение. Схема вместе с формой волны приведена ниже.
Мы подключили нагрузку (лампочку) с известным сопротивлением 1 кОм последовательно с конденсатором 470 мкФ, чтобы сформировать RC-цепь. Схема питается от батареи 12 В, а переключатель используется для замыкания и размыкания цепи. Форма волны измеряется через лампочку нагрузки и показана желтым цветом на изображении выше.
Первоначально, когда переключатель разомкнут, максимальное напряжение (12 В) появляется на резистивной нагрузке лампочки (Vr), и напряжение на конденсаторе будет нулевым. Когда переключатель замкнут, напряжение на резисторе упадет до нуля, а затем, когда конденсатор заряжается, напряжение вернется к максимуму, как показано на графике.
Время, необходимое для зарядки конденсатора, определяется формулой T = 5Ƭ, где “Ƭ” представляет tou (постоянная времени).
Давайте посчитаем время, за которое наш конденсатор заряжается в цепи.
Ƭ = RC = (1000 * (470 * 10 ^ -6)) = 0,47 секунды T = 5 = (5 * 0,47) T = 2,35 секунды.
Мы подсчитали, что время, необходимое для зарядки конденсатора, составит 2,35 секунды, то же самое можно проверить на графике выше. Время, необходимое для достижения Vr от 0 В до 12 В, равно времени, необходимому для зарядки конденсатора от 0 В до максимального напряжения. График иллюстрируется курсорами на изображении ниже.

Аналогичным образом мы также можем рассчитать напряжение на конденсаторе в любой момент времени и ток через конденсатор в любой момент времени, используя следующие формулы
V (t) = V B (1 — e -t / RC) I (t) = I o (1 — e -t / RC)
Где V B — напряжение батареи, а I o — выходной ток схемы. Значение t — это время (в секундах), в течение которого необходимо рассчитать значение напряжения или тока конденсатора.
Активное сопротивление R в цепи переменного тока
Что нам интересно знать про простейшую электрическую цепь содержащую R ?
Какой ток протекает в ней, какое напряжение на ней действует? и какая мощность может быть получена.
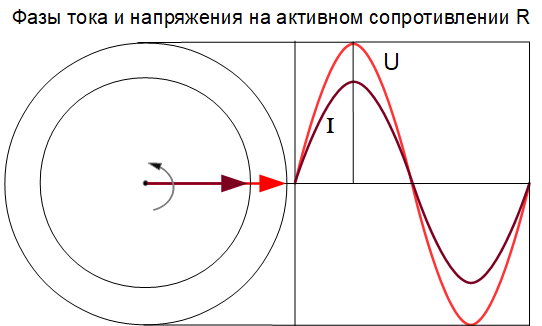
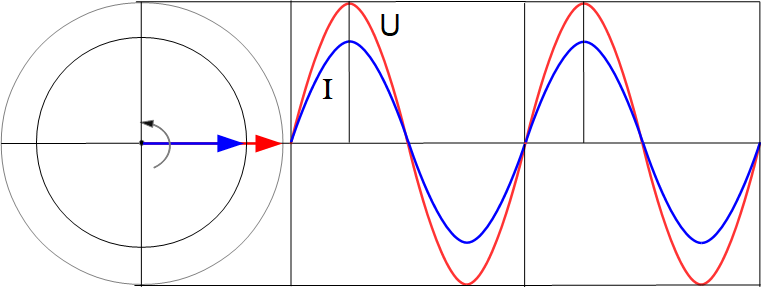
Здесь изображены две синусоиды, которые нельзя сравнивать и говорить какая больше, какая меньше. Они разные для удобства рассмотрения. Красная синусоида изображает переменное напряжение, а синяя синусоида изображает переменный ток
Если через активное R сопротивление протекает переменный синусоидальный ток, то на нем действует переменное синусоидальное напряжение. Ток и напряжение имеют одинаковую частоту и совпадают по фазе.
Мощность на активном сопротивлении определяется как произведение тока и напряжения. Действующая мощность будет равна произведению действующего значения тока на действующее значение напряжения.
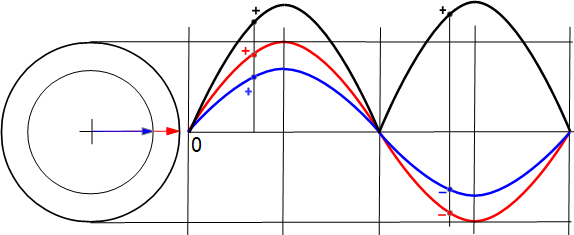
Черные полуволны показывают, что мощность выделяемая в цепи на активном сопротивление изменяется также по синусоидальному закону,
Только знак остается все время положительным, это значит, что поток мощности однонаправлен. Мощность получается как произведение каждой точки синусоиды тока на каждую точку синусоиды напряжения в один и тот же момент. Плюс напряжения на плюс тока даст нам плюс мощности. Минус напряжения на минус тока даст нам плюс мощности.
Это значит, что при протекании тока через активное сопротивление R, электрическая мощность приводит к выделению тепла.
P=UI U = Uа√2 ; I = Iа√2 P = UаIа/2
Средняя мощность за период равна постоянной составляющей мощности
Uа Iа/2
Физический смысл этого явления состоит в том, что активное сопротивление потребляет энергию от источника, выделяет энергию в виде тепла. Электрическая мощность, которая превращается в тепло, называется активной мощностью и обозначается, как и в цепях постоянного тока, буквой P
Активными сопротивлениями в цепях переменного тока являются нагревательные и осветительные приборы, а также резисторы в сигнальных схемах, кроме того, как активные сопротивления проявляют себя все устройства, на которых выделяется полезная мощность в любом виде. Например, электрический мотор, звуковые динамики и т. п.























