Теория вероятностей: формулы, примеры и онлайн-калькулятор

Почему важна вероятность?

Вы ежедневно используете или видите вероятность вокруг себя. Даже если вы этого не осознаете, вы каждый день используете вероятность, чтобы принимать решения о вещах с неизвестным исходом. Вы можете неосознанно выполнять математические расчеты с теоретической или экспериментальной вероятностью или делать выводы с субъективной вероятностью. Вот несколько реальных примеров того, как вы можете использовать или видеть вероятность каждый день:

Погода

Метеорологи не могут точно предсказать погоду, поэтому они используют приборы и инструменты, чтобы определить вероятность снега, дождя или других погодных условий. Если вероятность дождя составляет 30 %, метеоролог определил вероятность дождя так, что дождь шел 30 из 100 дней с аналогичными погодными условиями. Из-за прогноза вы используете вероятность, чтобы решить, надеть ли утром на работу сандалии или резиновые сапоги.

Спортивный

Тренеры и спортсмены часто используют вероятность, чтобы определить лучшие спортивные стратегии для соревнований и игр. Например, если футбольный кикер забивает 10 из 15 бросков с игры в течение сезона, вероятность того, что он забьет свой следующий бросок с игры, составляет 10/15 или 2/3. Другим примером является бейсбольный тренер, вычисляющий средний результат игрока, чтобы определить состав на игру. Если игрок имеет среднее количество боев 300, это означает, что он получил три удара из каждых 10 летучих мышей, а вероятность того, что он получит базовый удар, составляет 3/10.

Страхование

При анализе страховых полисов и рассмотрении вычитаемых сумм вероятность играет важную роль. Например, если 20 из каждых 100 водителей в вашем районе пострадали от града за последний год, то при выборе полиса автострахования вы можете использовать вероятность, чтобы понять, что вероятность того, что ваш автомобиль пострадает от града, равна 1/5. Эта значительная вероятность может побудить вас получить полное покрытие ущерба от града и, возможно, даже меньшую франшизу.

Игры

Когда вы играете в игры с элементом удачи или случайности, такие как настольные игры, карточные игры или видеоигры, вы часто взвешиваете шансы на желаемое событие, например, получение нужной карты или выпадение определенного числа на кубике. Вероятность того, что произойдет это благоприятное событие, поможет вам определить, когда рисковать или насколько вы готовы рискнуть. Одним из примеров являются игроки в покер, которые знают вероятность получения определенных рук, например, вероятность получения двух одинаковых рук составляет 42%, а вероятность получения трех одинаковых – 2%.

Вероятностно-статистическое объяснение мира

Определение 3

Вероятностно-статистический закон – это закон, который управляет поведением большой совокупности и который позволяет по отношению к индивидуальному объекту делать только вероятностные, то есть неоднозначные заключения, касающиеся его поведения.

Следует обратить внимание, что данным законом характеризуется поведение не отдельного элемента внутри коллектива, а поведение целостного коллектива. Знание статистической закономерности при этом не дает возможности однозначно предсказать поведение отдельных индивидуальных объектов, которые включены в коллектив. По отношению к отдельным элементами, такие предсказания носят исключительно вероятностный характер

По отношению к отдельным элементами, такие предсказания носят исключительно вероятностный характер.

Хорошим примером этого является закон распределения молекул по скоростям Максвелла. Данный закон, по мнению физиков, ничего определенного не говорит о скорости каждой отдельно рассматриваемой молекулы, взятой в определенный момент времени. Этот закон только устанавливает долю молекул, которым характерна абсолютно определенная скорость, среди других молекул, имеющихся в данном пространстве. Единственное, что можно сказать о скорости какой-то конкретно взятой молекулы – это предположение, что она обладает определенной скоростью в данный момент времени.

Классическая физика преимущественно сталкивается с законами динамического типа, и абсолютизация такого типа законов привела к концепции лапласовского, механического детерминизма. Принято считать, что подлинные законы природы могут быть исключительно динамическими, а статистические законы появляются в качестве результата неполноты человеческого знания. При возникновении квантовой механики ситуация резко изменилась. Оказалось, что поведение квантово-механических объектов в принцип характеризуется действием статистических и вероятностных законов. Основное уравнение квантовой механики дает возможность из знания вероятности найти микрообъект и в один момент предсказать вероятность его пространственной локализации в любом другом моменте. Все попытки построения квантовой механики на основании законов динамического типа не принесли никаких успехов.

В статистических законах предсказания не достоверны, а имеют только вероятностный характер. Такой характер предсказаний обуславливается воздействием массы случайных факторов, играющих свою роль в статистических коллективах или массовых событиях. Например, большое число молекул в газе, число особей внутри популяции, число людей в определенном коллективе и пр.

Замечание 1

Статистическая закономерность формируется в результате взаимодействия большого числа элементов, которые составляют коллектив, и поэтому характеризует не поведение отдельного элемента, а преимущественно коллектив в целом.

Статистические законы, несмотря на то, что не дают однозначных и достоверных предсказаний, являются тем не менее единственного возможными в процессе исследования массовых явлений случайного характера. За совокупным действием разных факторов случайного характера, которые практически не могут быть охвачены, статистическими законами вскрывается нечто устойчивое, необходимое и повторяющееся. Они являются подтверждением диалектики превращения случайностей в необходимое. Динамические законы являются предельным случаем статистических, когда вероятность превращается практически в достоверность.

В статистических законах предсказаниям свойственен не достоверный, а только вероятностный характер, который обуславливается воздействием большого количества случайных факторов, через сложное переплетение которых и выражается необходимость.

Вероятностно-статистические методы широко применяются в процессе изучения массовых, а не отдельных явлений случайного характера, например, в квантовой механике, статистической физики, синергетики, социологии и пр. На сегодняшний день все чаще можно услышать о проникновении вероятностного стиля мышления в науку. Ни в природе, ни в обществе не существует беспричинно возникающих явлений, все в мире так или иначе причинно обусловлено. Такая причинная взаимосвязь существует в мире объективно, вне зависимости от воли и сознания человечества. Например, нагревание металла является причиной такого явления, как его расширение.

Структурные элементы

Главная

§ 1. Понятие, задачи и функции уголовного права
§ 2. Принципы уголовного права
§ 3. Наука уголовного права
Вопросы для самоподготовки
Список рекомендованной литературы

§ 1. Понятие и содержание уголовной ответственности
§ 2. Начало и окончание уголовной ответственности
§ 3. Основание уголовной ответственности
Вопросы для самоподготовки
Список рекомендованной литературы

§ 1. Понятие уголовного закона
§ 2. Структура статьи уголовного закона
§ 3. Действие уголовного закона во времени
§ 4. Действие уголовного закона в отношении лиц, совершивших преступления на территории Российской Федерации
§ 5. Действие уголовного закона в отношении лиц, совершивших преступления за пределами Российской Федерации
§ 6. Толкование уголовного закона
Вопросы для самоподготовки
Список рекомендованной литературы

§ 1. Понятие и признаки преступления
§ 2. Разграничение преступлений и иных деликтов
§ 3. Категории преступлений
Вопросы для самоподготовки
Список рекомендуемой литературы

§ 1. Понятие, структура и значение состава преступления
§ 2. Классификация составов преступления
Вопросы для самоподготовки
Список рекомендованной литературы

§ 1. Понятие и значение объекта преступления
§ 2. Классификация объектов преступления
§ 3. Предмет преступления
Вопросы для самоподготовки
Список рекомендованной литературы

§ 1. Понятие и значение объективной стороны преступления
§ 2. Общественно опасное деяние
§ 3. Общественно опасные последствия преступления
§ 4. Причинная связь
§ 5. Место, время, способ и другие обстоятельства совершения преступления
Вопросы для самоподготовки
Список рекомендованной литературы

§ 1. Понятие и признаки субъекта преступления
§ 2. Невменяемость как обстоятельство, исключающее уголовную ответственность
§ 3. Специальный субъект преступления
§ 4. Уголовная ответственность лиц, совершивших преступление в состоянии опьянения
Вопросы для самоподготовки
Список рекомендованной литературы

§ 1. Понятие субъективной стороны преступления
§ 2. Вина как признак субъективной стороны преступления
§ 3. Умысел как форма вины
§ 4

Неосторожность как форма вины
§ 5. Мотив и цель общественно опасного деяния
§ 6

Ошибка в уголовном праве и ее влияние на содержание вины
Вопросы для самоподготовки
Список рекомендованной литературы

§ 1. Понятие неоконченного преступления
§ 2. Приготовление к преступлению
§ 3. Покушение на преступление
§ 4. Добровольный отказ от преступления
Вопросы для самоподготовки
Список рекомендованной литературы

§ 1. Понятие соучастия
§ 2. Виды соучастников
§ 3. Формы соучастия
§ 4. Ответственность соучастников
Вопросы для самоподготовки
Список рекомендованной литературы

§ 1. Понятие, виды и значение множественности преступлений
§ 2. Совокупность преступлений
§ 3. Рецидив преступления
Вопросы для самоподготовки
Список рекомендованной литературы

§ 1. Понятие и виды обстоятельств, исключающих преступность деяния
§ 2. Необходимая оборона
§ 3. Причинение вреда здоровью при задержании лица, совершившего преступление
§ 4. Крайняя необходимость
§ 5. Физическое или психическое принуждение
§ 6. Обоснованный риск
§ 7. Исполнение приказа или распоряжения
Вопросы для самоподготовки
Список рекомендованной литературы

§ 1. Понятие наказания по уголовному праву Российской Федерации
§ 2. Цели наказания
§ 3. Система наказаний
§ 4. Характеристика отдельных видов наказания.
Вопросы для самоподготовки
Список рекомендованной литературы

§ 1. Общие начала назначения наказания
§ 2. Назначение более мягкого наказания, чем предусмотрено за данное преступление
§ 3. Назначение наказания в особых случаях
§ 4. Условное осуждение
Вопросы для самоподготовки
Список рекомендованной литературы

§ 1. Понятие и основания освобождения от уголовной ответственности
§ 2. Виды освобождения от уголовной ответственности
§ 3. Амнистия
§ 4. Понятие и основания освобождения от наказания
§ 5. Виды освобождения от наказания
§ 6. Помилование. Судимость
Вопросы для самоподготовки
Список рекомендованной литературы

§ 1. Особенности уголовной ответственности несовершеннолетних
§ 2. Система и виды наказаний несовершеннолетних
§ 3. Освобождение несовершеннолетних от уголовной ответственности и наказания
Вопросы для самоподготовки
Список рекомендованной литературы

§ 1. Принудительные меры медицинского характера
§ 2. Конфискация имущества
§ 3. Судебный штраф
Вопросы для самоподготовки
Список рекомендованной литературы

Основные понятия

article>ФÑанÑÑзÑкие маÑемаÑики Ðлез ÐаÑÐºÐ°Ð»Ñ Ð¸ ÐÑÐµÑ Ð¤ÐµÑма анализиÑовали азаÑÑнÑе игÑÑ Ð¸ иÑÑледовали пÑÐ¾Ð³Ð½Ð¾Ð·Ñ Ð²ÑигÑÑÑа. Тогда они замеÑили пеÑвÑе закономеÑноÑÑи ÑлÑÑайнÑÑ ÑобÑÑий на пÑимеÑе бÑоÑÐ°Ð½Ð¸Ñ ÐºÐ¾ÑÑей и ÑÑоÑмÑлиÑовали ÑеоÑÐ¸Ñ Ð²ÐµÑоÑÑноÑÑей.

Ðогда Ð¼Ñ ÐºÐ¸Ð´Ð°ÐµÐ¼ монеÑкÑ, Ñо не можем ÑоÑно ÑказаÑÑ, ÑÑо вÑпадеÑ: оÑел или ÑеÑка.

Ðо еÑли подкидÑваÑÑ Ð¼Ð¾Ð½ÐµÑÑ Ð¼Ð½Ð¾Ð³Ð¾ Ñаз â окажеÑÑÑ, ÑÑо ÐºÐ°Ð¶Ð´Ð°Ñ ÑÑоÑона вÑÐ¿Ð°Ð´Ð°ÐµÑ Ð¿ÑимеÑно Ñавное колиÑеÑÑво Ñаз. Ðз Ñего можно ÑÑоÑмÑлиÑоваÑÑ Ð²ÐµÑоÑÑноÑÑÑ: 50% на 50%, ÑÑо вÑÐ¿Ð°Ð´ÐµÑ Â«Ð¾Ñел» или «ÑеÑка».

ТеоÑÐ¸Ñ Ð²ÐµÑоÑÑноÑÑей â ÑÑо Ñаздел маÑемаÑики, коÑоÑÑй изÑÑÐ°ÐµÑ Ð·Ð°ÐºÐ¾Ð½Ð¾Ð¼ÐµÑноÑÑи ÑлÑÑайнÑÑ Ñвлений: ÑлÑÑайнÑе ÑобÑÑиÑ, ÑлÑÑайнÑе велиÑинÑ, Ð¸Ñ ÑвойÑÑва и опеÑаÑии над ними.

Равновозможные события

Несколько событий в данном опыте называются равновозмож- ными, если по условиям симметрии есть основание считать, что ни одно из этих событий не является объективно более возможным, чем другое. Примеры равновозможных событий: 1) выпадение герба и выпадение цифры при бросании монеты; 2) появление 1, 3, 4, 5 очков при бросании игральной кости; 3) появление карты бубновой, червонной, трефовой масти при вынимании карты из колоды; 4) появление шара с № 1, 2, 3 при вынимании одного шара из урны, содержащей 10 перенумерованных шаров.

Существуют группы событий, обладающие всеми тремя свойствами: они образуют полную группу, несовместны и равновозможны; на- например: появление герба и цифры при бросании монеты; появление 1, 2, 3, 4, 5, 6 очков при бросании игральной кости. События, образующие такую группу, называются случаями (иначе «шансами»).

Если какой-либо опыт по своей структуре обладает симметрией возможных исходов, то случаи представляют собой исчерпывающую систему равновозможных и исключающих друг друга исходов опыта. Про такой опыт говорят, что он «сводится к схеме случаев» (иначе — к «схеме урн»).

Схема случаев по преимуществу имеет место в искусственно ор- организованных опытах, в которых заранее и сознательно обеспечена одинаковая возможность исходов опыта (как, например, в азартных играх). Для таких опытов возможен непосредственный подсчет вероятностей, основанный на оценке доли так называемых «благоприятных» случаев в общем числе случаев.

Случай называется благоприятным (или «благоприятствующим») некоторому событию, если появление этого случая влечет за собой появление данного события.

Например, при бросании игральной кости возможны шесть случаев: появление 1, 2, 3, 4, 5, 6 очков. Из них событию А—появлению четного числа очков — благоприятны три случая: 2, 4, б и не благоприятны остальные три.

Если опыт сводится к схеме, случаев, то вероятность события А в данном опыте можно оценить по относительной дело благоприятных случаев. Вероятность события А вычисляется как отношение числа благоприятных случаев к общему числу случаев: (2.2.1)

где Р (А) — вероятность события А; п — общее число случаев; m — число случаев, благоприятных событию А.

Так как число благоприятных случаев всегда заключено между О и п (—для невозможного и п—для достоверного события), то вероятность события, вычисленная по формуле 2.2.1), всегда есть рациональная правильная дробь: (2.2.2)

Формула (2.2.1), так называемая «классическая формула» для вы- вычисления вероятностей, долгое время фигурировала в литературе как определение вероятности. В настоящее время при определении (пояснении) понятия вероятности обычно исходят из других принципов, непосредственно связывая понятие вероятности с эмпирическим понятием частоты; формула же B.2.1) сохраняется лишь как формула для непосредственного подсчета вероятностей, пригодная тогда и только тогда, когда опыт сводится к схеме случаев, т. е. обладает симметрией возможных исходов.

Пример:

В урне находится 2 белых и 3 черных шара. Из урны на- наугад вынимается один шар. Требуется найти вероятность того, что этот шар будет белым.

Решение:

Обозначим А событие, состоящее в появлении белого шара. Общее число случаев п= 5; число случаев, благоприятных событию А, m = 2. Следовательно,

Пример:

В урне а белых и b черных шаров. Из урны вынимаются два шара. Найти вероятность того, что оба шара будут белыми.

Решение:

Обозначим В событие, состоящее в появлении двух белых шаров. Подсчитаем общее число возможных случаев п и число случаев m благоприятных событию В

следовательно,

Знаком обозначено число сочетаний из k элементов по l

Пример:

В партии из N изделий М бракованных. Из партии выбирается наугад п изделий. Определить вероятность того, что среди этих п изделий будет ровно m бракованных.

Решение:

Общее число случаев, очевидно, равно число благо- благоприятных случаев откуда вероятность интересующего нас события

Случайные события в повседневной жизни

В теории вероятности случайные события рассматриваются в абстрактном контексте, но они также являются неотъемлемой частью нашей повседневной жизни. Многие события, с которыми мы сталкиваемся каждый день, могут быть рассмотрены как случайные события.

1. Погода

Погода — это одно из самых ярких примеров случайного события в повседневной жизни. Мы не можем точно предсказать, будет ли сегодня солнечно или пасмурно, дождливо или сухо. В связи с этим, погода может быть рассмотрена как случайное событие.

2. Движение на дороге

Движение на дороге также является случайным событием. Мы не можем предсказать, когда и где произойдет авария или пробка. Поэтому, планируя свои поездки, мы учитываем вероятность возникновения непредвиденных ситуаций на дороге.

3. Очереди и задержки

Очереди и задержки — это еще один пример случайного события в повседневной жизни. Мы не можем предугадать, сколько времени уйдет на ожидание в очереди в магазине, банке или на почте. Также мы не всегда можем быть уверены, что поезд приедет вовремя или самолет вылетит без задержек.

4. Лотереи и азартные игры

Лотереи и азартные игры по своей сути основаны на случайных событиях. Выигрышные комбинации или исходы спортивных событий рассчитываются на основе вероятностей. Хотя шансы на выигрыш могут быть очень малыми, люди по-прежнему играют, надеясь на удачу и возможность стать обладателем большого выигрыша.

5. Аномальные ситуации

Некоторые случайные события в повседневной жизни могут иметь серьезные последствия. Например, наводнение, пожар, землетрясение — все эти события носят случайный характер и могут внезапно повлиять на нашу жизнь

В связи с этим, разработка планов аварийного поведения и мер безопасности является важной частью нашей готовности к таким случайным событиям

В конечном счете, случайные события окружают нас повсюду, и понимание их влияния и вероятностей помогает нам принимать осознанные решения и планировать действия в повседневной жизни.

Типы вероятности

Это четыре различных типа вероятности:

Классический

Классическая или теоретическая точка зрения на вероятность утверждает, что в эксперименте, где есть X равновероятных исходов, а событие Y имеет ровно Z этих исходов, тогда вероятность Y равна Z/X, или P(Y) = Z/X. Часто это первая перспектива, с которой учащиеся сталкиваются в формальном образовании. Например, при бросании честного кубика есть шесть возможных исходов, которые равновероятны, вы можете сказать, что вероятность выпадения каждого числа составляет 1/6.

Преимущество этой перспективы заключается в том, что она концептуально проста для многих ситуаций, однако у нее есть ограничения, поскольку многие ситуации не имеют конечного количества равновероятных результатов. Например, бросок взвешенного игрального кубика дает конечное число результатов, которые не равновероятны, или изучение доходов сотрудников в течение многих лет и в будущем дает бесконечное количество результатов для их максимально возможного дохода.

Эмпирический

Эмпирическая или экспериментальная точка зрения на вероятность определяет вероятность посредством мысленных экспериментов. Например, если вы бросаете взвешенный кубик, но не знаете, какая сторона имеет вес, вы можете получить представление о вероятности каждого исхода, бросив кубик огромное количество раз и подсчитав долю раз, когда кубик выпадет. дает этот результат и оценивает вероятность этого результата.

Формальный способ определить эту перспективу: P(A) = предел, когда C приближается к бесконечности B/C. Где A — вероятность события, B — количество раз, когда событие A происходит, а C — количество раз, когда вы выполняете процесс, например бросаете кубик или подбрасываете монету.

Другой способ подумать об этом — представить, что вы подбрасываете монету 100 раз, а затем продолжаете до 10 000 раз. Каждый раз, когда вы подбрасываете монету, реальные результаты вероятности, которые вы получаете, становятся лучшим приближением к теоретической вероятности события. Первые 100 раз, когда вы подбрасываете монету, ваша вероятность может составлять 1/3 орла, но чем больше вы будете подбрасывать по мере приближения к бесконечности, тем больше ваша вероятность станет 1/2, или теоретической вероятностью.

субъективный

Субъективный взгляд на вероятность рассматривает собственное личное убеждение или суждение человека о том, что событие произойдет. Например, у инвестора может быть образованное чувство рынка, и он может интуитивно говорить о вероятности завтрашнего роста определенных акций. Вы можете рационально понять, как этот субъективный взгляд согласуется с теоретическими или экспериментальными взглядами. Другими словами, это вероятность того, что то, что человек ожидает от своих знаний и чувств, на самом деле будет результатом, без каких-либо формальных расчетов.

Например, если болельщик на футбольном матче заявляет, что конкретная команда собирается выиграть игру, он основывает свое решение на прошлых победах и поражениях этой команды, на том, что он знает о команде соперника, на фактах, которые он знает о футболе и своих интересах. мнения или чувства по поводу игры. Они не делают формальных математических расчетов.

Аксиоматический

Аксиоматическая точка зрения на вероятность – это объединяющая точка зрения, в которой согласованные условия, используемые в теоретической и экспериментальной вероятности, доказывают субъективную вероятность. Вы применяете набор правил или аксиом Колмогорова ко всем типам вероятностей. Математикам они известны как три аксиомы Колмогорова. При использовании аксиоматической вероятности вы можете количественно оценить вероятность того, что событие произойдет или не произойдет.

Вы можете использовать эти три аксиомы со всеми другими перспективами вероятности. Определение этой точки зрения – это вероятность любой функции от чисел до событий, удовлетворяющей следующим трем аксиомам:

• Ноль — это наименьшая возможная вероятность, а единица — наибольшая.

• Вероятность достоверного события равна единице.

• Два взаимоисключающих события не могут произойти одновременно, но объединение событий говорит о том, что может произойти только одно из них.

Неопределенность

Неопределенность предполагает наличие факторов, при которых результаты действий не являются детерминированными, а степень возможного влияния этих факторов на результаты неизвестна. Например, это неполнота или неточность информации об условиях реализации проекта.

Факторы неопределенности подразделяются на внешние и внутренние. Внешние факторы – законодательство, реакция рынка на выпускаемую продукцию, действия конкурентов и др. Внутренние – компетентность персонала фирмы, ошибочность определения характеристик проекта и т.д.

Условия неопределенности, имеющие место при любых видах предпринимательской деятельности, объясняются тем, что экономические системы в процессе своего функционирования испытывают зависимость от ряда причин, которые можно систематизировать в виде схемы неопределенностей.

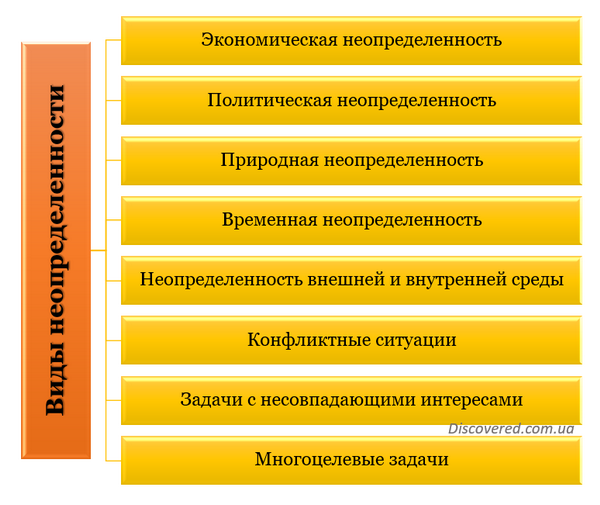Виды неопределенностей

По времени возникновения неопределенности делятся на ретроспективные, текущие и перспективные. Необходимость учета фактора времени при оценке экономической эффективности принимаемых решений связана с тем, что и эффект, и затраты могут быть распределены во времени. Равные по величине затраты, по-разному распределенные во времени, дают неодинаковый полезный результат того или иного вида (экономический, социальный и др.).

Рассматривая неопределенность как наиболее характерную причину риска в экономической, коммерческой, управленческой, финансовой и других видах деятельности, необходимо отметить, что выделение и изучение ее является крайне необходимым, поскольку на практике приходится сталкиваться с ситуациями, условия которых не могут быть однозначно определены.

В литературе существуют различные формулировки термина «неопределенность». Наиболее полная формулировка, такая: неопределенность – это неполное или неточное представление о значениях различных параметров в будущем, порождаемых различными причинами, прежде всего неполнотой или неточностью информации об условиях реализации решения, в том числе связанных с ними затратах и результатах.

С точки зрения вероятности осуществления событий неопределенность можно подразделить на три вида:

1. полная неопределенность;
2. полная определенность;
3. частичная неопределенность.

Полная неопределенность характеризуется близкой к нулю прогнозируемостью Р_t наступления события, что математически выражается соотношением

lim Рt = 0
t → tk

где t – время;t_k – конечное время прогнозирования события.

Полной определенности соответствует близкая к единице прогнозируемость событий, т.е.

lim Рt = 1
t → tk

Это возможно прежде всего в тех случаях, когда при решении задачи в условиях неопределенности определяется, с какой вероятностью оптимальное решение находится в доверительном прогнозируемом интервале, что позволяет владельцу бизнеса не только реализовывать свою стратегию на рынке, но и прогнозировать свое собственное поведение, тенденции развития рынка и т.п.

Частичная неопределенность отвечает таким событиям, прогнозируемость которых лежит в пределах от 0 до 1, что определяется неравенством

0 < lim Рt < 1
t → tk

В условиях объективного существования риска и связанных с ним финансовых, моральных и других потерь возникает потребность в определенном механизме, который позволил бы наилучшим из возможных способов с точки зрения поставленных предпринимателем (фирмой) целей учитывать риск при принятии решений и реализации хозяйственной деятельности.

Риску как экономической категории свойственна и такая характеристика, как противоречивость.