Нахождение целого числа по дроби
Зная часть числа и сколько это составляет от целого числа, можно найти изначальное целое число. Это обратная задача к той, которую мы рассматривали в предыдущей теме. Там мы искали дробь от числа, деля это число на знаменатель дроби, и полученный результат умножая на числитель дроби.
А сейчас наоборот, зная дробь и сколько это составляет от числа, найти изначальное целое число.
Например, если длины линейки составляют шесть сантиметров и нам говорят найти длину всей линейки, то мы должны понимать, что от нас требуют найти изначальное целое число (длину всей линейки) по дроби . Давайте решим эту задачу.
Требуется найти длину всей линейки по дроби . Известно, что длины всей линейки составляют 6 см.
Мы уже знаем каким образом получились эти 6 см. Имелась какая-то длина, её разделили на пять частей, поскольку знаменатель дроби это число 5. Затем было взято две части от пяти частей, поскольку числитель дроби это число 2.
Чтобы узнать длину всей линейки, сначала нужно узнать длину одной части. Как это узнать? Попробуем догадаться, внимательно изучив следующий рисунок:

Если две части длины линейки составляют 6 см, то нетрудно догадаться, что одна часть составляет 3 см. А чтобы получить эти 3 см, надо 6 разделить на 2
6 см : 2 = 3 см
Итак, мы нашли длину одной части. Одна часть из пяти или длины линейки составляет 3 см. Если частей всего пять, то для нахождения длины линейки, нужно взять три сантиметра пять раз. Другими словами, умножить 3 см на число 5
3 см × 5 = 15
Мы нашли длину линейки. Она составляет 15 сантиметров. Это можно увидеть на следующем рисунке.
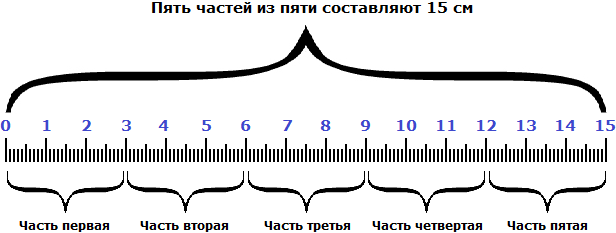
Видно, что пять частей из пяти или составляют пятнадцать сантиметров.
Чтобы легче было находить число по его дроби, можно пользоваться следующим правилом:
Чтобы найти число по его дроби, нужно известное число разделить на числитель дроби, и полученный результат умножить на знаменатель дроби.
Пример 2. Число 20 это от всего числа. Найдите это число.
Знаменатель дроби показывает, что число, которое мы должны найти, разделено на пять частей. Если этого числа составляет число 20, то для нахождения всего числа, сначала нужно найти (одну часть из пяти) от всего числа. Для этого 20 надо разделить на числитель дроби
20 : 4 = 5
Мы нашли от всего числа. Эта часть равна 5. Чтобы найти всё число, нужно полученный результат 5 умножить на знаменатель дроби
5 × 5 = 25
Мы нашли от всего числа. Другими словами, нашли всё число, которое от нас требовали найти. Это число 25.
Пример 3. Десять минут это времени приготовления каши. Найдите общее время приготовления каши.
Знаменатель дроби показывает, что общее время приготовления каши разделено на три части. Если времени приготовления каши составляет десять минут, то для нахождения общего времени приготовления, нужно сначала найти времени приготовления. Для этого 10 нужно разделить на числитель дроби
10 мин : 2 = 5 мин
Мы нашли времени приготовления каши. времени приготовления каши составляют пять минут. Для нахождения общего времени приготовления, нужно 5 минут умножить на знаменатель дроби
5 мин × 3 = 15 мин
Мы нашли времени приготовления каши, то есть нашли общее время приготовления. Оно составляет 15 минут.
Пример 4. массы мешка цемента составляет 30 кг. Найти общую массу мешка.
Знаменатель дроби показывает, что общая масса мешка разделена на четыре части. Если массы мешка составляет 30 кг то для того, чтобы найти общую массу мешка нужно сначала найти массы мешка. Для этого 30 надо разделить на числитель дроби .
30кг : 2 = 15кг
Мы нашли массы мешка. массы мешка составляет 15 кг. Теперь, чтобы найти общую массу мешка, надо 15кг умножить на знаменатель дроби
15кг × 4 = 60кг
Мы нашли массы мешка. Другими словами, нашли общую массу мешка. Общая масса мешка цемента составляет 60 кг.
Основные понятия и термины в математике
Математика — это наука, которая изучает количество, структуру, пространство и изменение.
Число — это математический объект, который используется для измерения количества или размерности.
Операция — это математическое действие, которое выполняется над числами или другими математическими объектами.
Функция — это математический объект, который связывает каждый элемент из одного множества с элементами другого множества.
Геометрия — это наука, которая изучает пространственные формы, размеры и их связи.
Треугольник — это геометрическая фигура, которая состоит из трех линий, называемых сторонами, и трех углов между сторонами.
Дробь — это число, которое представлено как отношение одного целого числа к другому.
Пропорция — это соотношение двух дробей или отношение двух отрезков.
- Декартова система координат — это способ представления точек на плоскости или в пространстве с помощью координат.
- Уравнение — это математическое выражение, которое утверждает равенство двух выражений.
- Интеграл — это математический объект, который используется для нахождения площади под кривой на графике.
Вектор — это математический объект, который имеет направление и длину и может использоваться для представления движения или силы.
Матрица — это таблица чисел или символов, которая используется для представления линейных уравнений и преобразований.
ТерминОписание
| Логарифм | Метод для измерения количества, используемый для решения уравнений. |
| Производная | Мера изменения функции по отношению к изменению ее аргумента. |
| Измерение | Процесс оценки размера, количества и веса объекта. |
Примеры использования одной трети в повседневной жизни
Одна треть — это дробь, значение которой равно одному делению числа на три. В нашей повседневной жизни мы можем встретить различные примеры, когда одна треть играет важную роль.
-
Сон и время отдыха: Одна треть суток составляет 8 часов, что является рекомендованным временем сна для взрослого человека. Высыпаясь полностью, мы даем своему организму необходимую треть времени для восстановления и отдыха.
-
Питание: Правильное питание предполагает, что одна треть нашей пищи должна состоять из овощей и фруктов. Такое соотношение позволяет обеспечить организм необходимыми витаминами и минералами.
-
Работа и отдых: Есть принятая формула «8 часов работа, 8 часов отдых, 8 часов свободное время». Она предполагает, что одна треть нашего дня должна быть посвящена отдыху и занятиям, которые доставляют нам удовольствие.
-
Объемы жидкости: Рекомендуется пить не менее одной трети литра воды в течение дня, чтобы поддерживать равновесие водного баланса в организме.
-
Время использования техники: Рекомендуется делать перерыв каждые 20-30 минут работы за компьютером или использования другой техники. В таком случае одна треть времени будет посвящена отдыху глаз и предотвращению стресса.
Это лишь несколько примеров, где одна треть играет важную роль
Важно помнить о пропорции и балансе в жизни, чтобы добиться здоровья, гармонии и эффективности в различных областях
Как использовать обозначение целой части числа в математических выражениях?

Обозначение целой части числа в математических выражениях играет важную роль при решении различных задач. С помощью этого обозначения легко выделять и использовать только целые значения, что удобно при работе с результатами измерений, денежными суммами или любыми другими значениями, где важна только целая часть числа. Например, если у вас есть список продуктов и их цен в рублях, вы можете использовать обозначение целой части числа, чтобы оценить стоимость всего списка без учета копеек.
Одним из самых простых и распространенных способов использования обозначения целой части числа в математических выражениях является округление числа до ближайшей целой. Например, если у вас есть число 5.7, вы можете округлить его до 6, чтобы использовать только целую часть в своих вычислениях. Это особенно полезно в ситуациях, когда требуется получить простое и легко интерпретируемое число, например, при подсчете количества чего-либо или при анализе данных.
- Просто округлите число до ближайшей целой, отбрасывая дробную часть.
- Если число положительное и имеет десятичную часть больше или равную 0.5, то округлите число вверх до ближайшей целой.
- Если число положительное и имеет десятичную часть меньше 0.5, то округлите число вниз до ближайшей целой.
- Если число отрицательное и имеет десятичную часть больше или равную -0.5, то округлите число вниз до ближайшей целой.
- Если число отрицательное и имеет десятичную часть меньше -0.5, то округлите число вверх до ближайшей целой.
Использование обозначения целой части числа в математических выражениях позволяет сосредоточиться на главном значении и упростить вычисления. Округление и отбрасывание дробной части числа часто используются для получения более удобных и понятных результатов. Различные правила округления могут быть применены в зависимости от контекста и требований задачи
Как и во всех математических операциях, важно следить за правильностью и точностью округления, чтобы избежать ошибок и искажений результатов
Случаи расчета двух и трех частей в математике
Расчет двух и трех частей появляется в математике в различных контекстах и задачах. В общем, двух и трех частей можно понимать как разбиение некоторого целого числа на две или три равные (или не равные) части.
Один из самых распространенных случаев расчета двух и трех частей связан с долями и процентами. Например, если вас просят поделить некоторую сумму денег на две или три части в соответствии с заданными процентными долями каждой части, вы можете использовать формулы пропорций или просто найти соответствующее значение для каждой части.
Другой случай, когда возникает расчет двух и трех частей, связан с геометрией и разбиением фигур на части. Например, при разбиении прямоугольника на две или три части можно использовать геометрические пропорции или формулы площади, чтобы найти размеры каждой части.
Расчет двух и трех частей также может появляться в задачах, связанных с вероятностным распределением. Например, если вас просят разбить некоторую выборку на две или три части в соответствии с заданными вероятностными долями каждой части, вам нужно будет использовать формулы вероятности или другие методы статистического анализа.
В целом, расчет двух и трех частей может быть полезным для решения различных задач в математике и других областях знания. Но в каждом конкретном случае необходимо выбирать подходящий метод и формулы в соответствии с заданными условиями и требованиями.
Важные моменты при расчете одной трети числа
Во-первых, десятичная запись одной трети числа может быть бесконечной
Поэтому важно определить, какую точность вы хотите использовать при округлении ответа. Если вам нужен точный результат, лучше использовать десятичные дроби или выполнить расчет с дополнительными знаками после запятой
Во-вторых, при выполнении операции деления числа на треть, обратите внимание на возможность получения бесконечно большого значения. Если число, которое вам нужно разделить, очень большое, то результат такой операции может быть очень великим и трудно интерпретируемым
Также стоит учитывать, что при делении числа на треть результат может быть нерациональным числом. Это означает, что десятичная запись такого числа будет не периодической и неокругляемой.
Важно помнить, что при работе с десятичными дробями всегда возможно округление результата. Выберите нужный метод округления в соответствии с требованиями задачи
Например, вы можете использовать округление вниз, вверх или до ближайшего целого числа.
Наконец, не забывайте учитывать порядок операций, особенно если вам нужно вычислить одну треть числа, когда это число также является результатом другой математической операции. Учтите все предыдущие действия, чтобы получить точный ответ.
Важные моменты при нахождении 1/3 числа:
Определите необходимую точность результатов
Учтите возможность получения очень большого значения
Обратите внимание на возможность получить нерациональное число
Выберите метод округления результата
Учитывайте порядок предыдущих операций
Правило встречается в следующих упражнениях:
3 класс
Страница 96,Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 38. ПР 5. Вариант 1,Моро, Волкова, Проверочные работы
Страница 45. Тест 2. Вариант 2,Моро, Волкова, Проверочные работы
Страница 28,Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 45,Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 70,Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 100,Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 26,Моро, Волкова, Рабочая тетрадь, часть 2
Страница 46. Урок 17,Петерсон, Учебник, часть 1
Страница 94. Урок 41,Петерсон, Учебник, часть 2
4 класс
Страница 19,Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 49,Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 88,Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 90,Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 9,Моро, Волкова, Рабочая тетрадь, часть 1
Страница 76,Моро, Волкова, Рабочая тетрадь, часть 1
Страница 65,Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 84,Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 98,Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 76,Моро, Волкова, Рабочая тетрадь, часть 2
5 класс
Задание 216,Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 82,Мерзляк, Полонский, Якир, Учебник
Номер 83,Мерзляк, Полонский, Якир, Учебник
Номер 2,Мерзляк, Полонский, Якир, Учебник
Значимость знания двух и трех частей в математике для повседневной жизни
Математика является одним из самых важных предметов в нашей жизни. Знание двух и трех частей в математике помогает нам понимать мир вокруг нас, рассчитывать расходы, прогнозировать результаты и многое другое.
Рассчеты в финансовой и бизнес-сферах
В современном мире наши финансовые решения зависят от математических вычислений. При покупке товаров и услуг мы должны рассчитывать стоимость и оценивать свои расходы. Если вы владеете знанием двух и трех частей в математике, то сможете быстрее и точнее рассчитать сумму, которую вы потратите.
Практическое применение математики в жизни
Кроме финансов, математика помогает нам решать множество повседневных задач. Например, знание процентов и долей может помочь вам рассчитать пропорции ингредиентов для приготовления блюда.
- Кроме того, знание двух и трех частей позволяет рассчитывать время, необходимое для выполнения задач и выработки навыков продуктивности.
- Знание геометрических форм может быть полезным при решении ежедневных задач, таких как перестановка мебели или монтаж рамок.
- Понимание математических принципов также может помочь вам в развитии логического мышления и принятии обоснованных решений.
Кратко говоря, знание двух и трех частей в математике необходимо для повседневной жизни. Эти знания помогают нам в финансах, бизнесе и многих других областях.
1/4 (одна четвертая) часть
Это значит, что целое поделили на 4 равные части, а затем взяли одну из них. Например:
Сколько составляет 1/4 в процентах:
Отсюда, одна четвертая часть чего-либо будет равна 25 процентам.
Например: 1/4 доли в квартире — это 25% от её общей площади.
Проценты обозначаются таким знаком %.
Один процент — это одна сотая часть (1/100) или же 0,01.
Соответственно 15 процентов — это 15/100 или же 0,15.
Дробь 15/100 мы можем сократить на 5 и получим 3/20.
Теперь перейдем к нашим дробям.
Дробь 1/2 — это 50/100 (мы умножили числитель и знаменатель на 50, чтобы знаменатель получился равным 100) или же 50 процентов.
Дробь 1/4 — это 25/100 (мы умножили числитель и знаменатель на 25) или же 25 процентов.
С дробью 1/3 будет посложнее, так как знаменатель не получится умножить на целое число, чтобы получилось 100. Получается 33 целых и 33 сотых процента.
1/2 это половина целого или 0,5, чтобы получить процент, умножаем 0,5на 100 — получаем 50 % как это получить — нужно разделить числитель на знаменатель и умножить на 100.
Одна треть 1/3 может быть записана как 0,333, мы выполнили действие деления и умножаем 0,333 на 100 = 33,3 %
1/2=50%
1/3=33,3%
1/4=0,25%
На самом деле перевести обыкновенную дробь в проценты достаточно легко.
Значение, выраженное в процентах будет просто в 100 раз больше, чем в долях.
Проценты для удобства обычно не пишут дробями, поэтому 1/2, 1/3 и 1/4 нужно сначала перевести в десятичную дробь, потом умножить на 100%.
Как известно, процент — это сотая часть чего-то, т.е. 1/100 или 0,01.
Поэтому для нахождения указанных в вопросе долей, надо соотнести их с одной сотой.
1/2 составляет половину исходной единицы, а в сотых долях это будет 50/100 и, следовательно, 50%.
1/3, как треть от целого, перевести в проценты сложнее, потому что 100 не делится на 3 без остатка — поэтому считается, что это будет приблизительно 33/100, т.е. 33%.
1/4 — это четверть исходной единицы, равная 25/100, которые легко преобразуются в 25%.
Если у нас есть целое
Давайте наверное опять начну с аксиом (истин). Ведь строить выводы без догм (истин), это все равно, что дом без фундамента. Нам известно о том, что есть целое, то есть что-то единое, что мы привыкли считать по 1, применять к нему термин 100 процентов, представлять как нечто обособленное, отдельное если хотите. Заметьте, что не смотря на то, что мы имеем что-то целое, это не значит, что его нельзя разобрать на части. Я думаю так делали многие дети, а в прошлом их родители, когда отрывали колесики от целой машинки или руки от пластиковых пупсиков… Ну, а опять же самый ходовой пример, это откусить часть от яблока.

И именно здесь пришло то самое время, дабы поговорить уже о частях целого!
Разделение чисел в памяти компьютера
Компьютеры не хранят числа в обычной десятичной форме, как мы привыкли. Вместо этого, числа в компьютере хранятся и обрабатываются в двоичной системе счисления. Это означает, что каждое число разбивается на отдельные биты, которые в свою очередь представляются двоичными цифрами 0 и 1.
Обычно, числа в компьютере хранятся в виде типов данных, таких как integer (целые числа), float (числа с плавающей точкой) и double (двойная точность числа с плавающей точкой). Каждый тип данных имеет свой размер в памяти и свой формат представления чисел.
Целочисленные типы данных, такие как int, short и long, хранят целые числа без дробной части. В памяти, целые числа представляются в виде двоичных чисел. Например, число 5 в десятичной системе будет представлено в памяти компьютера как 00000101.
Типы данных с плавающей точкой, такие как float и double, хранят числа с дробной частью. В памяти, числа с плавающей точкой представляются с использованием формата называемого «числа с плавающей точкой». Этот формат разделен на две части — мантиссу и порядок. Мантисса представляет собой дробную часть числа, а порядок указывает, на сколько нужно сдвинуть мантиссу, чтобы получить исходное число.
Разделение чисел в памяти компьютера является очень важным для правильного хранения и обработки чисел. Разные типы данных имеют разное количество бит, выделяемое для хранения чисел, что влияет на диапазон значений, которые могут быть представлены.
Понимание разделения чисел в памяти компьютера очень полезно для разработчиков программного обеспечения, так как позволяет избежать ошибок и неэффективного использования памяти. Кроме того, знание о разделении чисел помогает лучше понять, как компьютер обрабатывает числа и выполняет арифметические операции.
Вопрос-ответ:
Как сократить дробь?
Для того чтобы сократить дробь a/b, нужно найти такую общую делимость a и b и поделить их на нее. Например, дробь 6/9 можно сократить до 2/3, разделив числитель и знаменатель на 3.
Что такое десятичная дробь?
Десятичная дробь – это дробь вида a/10^b, где a и b – целые числа. Например, дробь 3/1000 – это десятичная дробь, так как ее можно записать как 0,003.
Как перевести десятичную дробь в обыкновенную?
Для перевода десятичной дроби в обыкновенную нужно записать дробь так, чтобы знаменатель был степенью 10. Например, десятичную дробь 0,25 можно записать как 25/100, а затем сократить до 1/4.
Как сложить две дроби?
Для сложения двух дробей нужно привести их к общему знаменателю, затем сложить числители и записать результат в виде несократимой дроби. Например, чтобы сложить 1/3 и 2/5, нужно привести дроби к общему знаменателю 15: 1/3 = 5/15, 2/5 = 6/15. Затем суммируем числители: 5/15 + 6/15 = 11/15.
Как умножить две дроби?
Для умножения двух дробей нужно умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй дроби, затем записать результат в виде несократимой дроби. Например, чтобы умножить 2/3 на 4/5, нужно выполнять следующие действия: 2/3 * 4/5 = (2 * 4)/(3 * 5) = 8/15.
Что такое дроби с отрицательным знаменателем?
Дробь с отрицательным знаменателем – это дробь, у которой знак числителя и знаменателя разные. Например, дробь -2/3. Такую дробь можно преобразовать к дроби с положительным знаменателем, поменяв знаки числителя и знаменателя местами: -2/3 = 2/-3.
Способы использования одной трети от суммы в управлении финансами
Одна треть от суммы может быть использована в управлении финансами различными способами. Ниже представлены несколько из них:
- Сбережения. Одна треть от суммы может быть отложена на сберегательный счет или вклад, чтобы создать финансовую подушку на случай неожиданных расходов или для достижения долгосрочных целей.
- Инвестиции. Одна треть от суммы может быть инвестирована в акции, облигации или другие финансовые инструменты для получения дополнительного дохода или роста капитала.
- Погашение долгов. Если у вас есть долги, то одна треть от суммы может быть использована на их погашение. Это поможет снизить общую сумму задолженности и уменьшить затраты на проценты.
- Повышение финансовой грамотности. Одна треть от суммы может быть потрачена на обучение и повышение своих знаний о финансовых инструментах, инвестировании или управлении бюджетом. Это поможет вам принимать более осознанные и обоснованные финансовые решения.
- Путешествия и развлечения. Одна треть от суммы может быть использована на путешествия, развлечения и хобби. Это поможет вам насладиться жизнью и получить удовольствие от достигнутых финансовых результатов.
Выбор способа использования одной трети от суммы зависит от ваших финансовых целей, приоритетов и обстоятельств.
Значение слова треть
треть
треть — то же, что одна третья (⅓) — доля, дробь. Также может означать:
ж.Одна из трех равных частей, на которые делится что-либо.
Большой современный толковый словарь русского языка
ж. Одна из трех равных частей, на которые делится что-л.
Новый толково-словообразовательный словарь русского языка Ефремовой
одна из трех равных частей, на которые делится что-нибудь Т. года. Две трети.
Словарь русского языка Ожегова
ж. Одна из трех равных частей, на которые делится что-л.
Толковый словарь Ефремовой
трети, мн. трети, третей, ж. Одна из трех равных частей, на к-рые делится что-н. Треть пути. Треть работы. Треть года. Вперед ему треть жалованья выдать! Пушкин.
Полный орфографический словарь русского языка
каждая из трёх равных частей целого
Треть её состава назначена президентом, другая треть выбрана этой президентской третью и, наконец, последняя треть – из провинции, то есть прошла через сито отбора губернаторами и местными депутатами.
Треть войска с ним во главе воевала с местными жителями, вторая треть с кормчим охраняла корабль, а третья треть с воином, место которого было на носу корабля, разрушила курган, и добыли они много сокровищ.
Все годы, что я ее знал, а тому уже пятнадцать лет, бедная женщина треть своего времени проводит за готовкой, вторую треть — в ожидании прихода рабочего из товарищества владельцев квартир, который — она в этом была убеждена — установит почтовые ящики, чтобы ей не приходилось больше заниматься корреспонденцией, а последнюю треть — сплетничая с мадам Фреон, вдовой с третьего этажа.
Чехословакия потеряла треть своей территории вместе с третью населения, в том числе почти полутора миллионами чехов, словаков и украинцев, треть промышленного потенциала.
Вожди усташей ставили задачу вполне определенно: треть сербов истребить, другую треть окатоличить, третью – изгнать.
Первую треть времени общения Внучок отчитывался, вторую треть Михаил посвящал постановке задачи, а третью — попыткам вдолбить в не отягощенную интересом голову хоть какие-то азы системного анализа.
Таким образом, путём несложной тюремной арифметики получаем: если одна треть целого – это 90 человек, то три третьих есть 3 х 90 = 270 человек.
К сорока годам скопив запланированную сумму в иностранной валюте, тихо отошел от дел, каким-то образом ухитрился избежать ликвидации, треть денег вложил в недвижимость, треть в процветающую фирму, а еще треть разместил на счетах надежных заграничных банков.
Когда же Фунан оторвал руки от лица и посмотрел, из призрачного пятна уже образовалось нечто плотное — безумный кошмар, что казался на треть человеком, на треть рептилией и на треть демоническим зверем.
Лев Давидович Ландау
Сергей Сергеевич Бодров
Зенон Станиславович Позняк
Как добавить примеры дробей?
Как вы показываете дроби в работе?
Как научить ребенка дробям?
Почему мы используем дроби? Дроби важны, потому что они говорят вам, какая часть целого вам нужна, есть или вы хотите. Фракции используются в выпечке, чтобы сказать, сколько ингредиентов использовать. Дроби используются для определения времени; каждая минута — это доля часа.
Что такое дробь простыми словами?
A дробь просто говорит нам, сколько частей целого у нас есть. Вы можете распознать дробь по косой черте, написанной между двумя числами. У нас есть верхнее число, числитель, и нижнее число, знаменатель. Например, 1/2 — это дробь. … 1 — это числитель, а 2 — знаменатель.
Какой процент составляет треть? Конвертер величин. / Конвертер дробей и процентов, Дроби ** одна треть или . (3): 1. … Проценты и доли.
| одна треть или .(3) → процентов (%) | 33.33 |
|---|---|
| одна треть или .(3) → частей на миллион (ppm) | 333,333 |
Сколько процентов составляет треть?


























