Обыкновенные дроби

Введение и распространение

Полнолуние

Юлий Цезарь

В современной неделе семь дней. Это самая большая общепринятая единица времени, содержащая точное количество дней.

Совет­ский учёный-хронолог И. А. Кли­ми­шин пола­гал, что подоб­ная мера вре­ме­ни свя­за­на с изме­не­ни­ем фазы Луны: «В самом деле, про­дол­жи­тель­ность сино­ди­че­ско­го меся­ца состав­ля­ет 29,53 суток, при­чём люди виде­ли Луну на небе око­ло 28 суток: семь дней про­дол­жа­ет­ся уве­ли­че­ние фазы Луны от узко­го сер­па до пер­вой чет­вер­ти, при­мер­но столь­ко же — от пер­вой чет­вер­ти до пол­но­лу­ния и так далее». Можно считать, что недели образуют независимый календарь, используемый одновременно с различными другими календарями. В I веке неделя вытеснила восьмидневный римский базарный цикл нундины благодаря календарной реформе Юлия Цезаря. Ею стали пользоваться в Древнем Риме. Потом семидневная неделя распространилась по всей Западной Европе. Позже из-за европейской колонизации и последующей глобализации семидневная неделя стала применяться везде, даже в тех культурах, у которых такой единицы времени раньше не было. С юридической точки зрения неделя впервые упоминается в кодексе Феодосия (321 год нашей эры).

Алгоритм Евклида для вычисления НОД (наибольшего общего делителя)

Не всегда, сходу, можно понять какое число является наибольшим общим числителем, особенно если числа крупные, поэтому существует специальный алгоритм для выведения такого числа НОД.

Суть алгоритма такова: для нахождения НОД чисел а и b (где они целые и положительные числа, к тому же a больше b), выполняется ряд делений с остатком, получается ряд равенств, где деление останавливается в том случае если r_k+1=0, при этом r_k=НОД(a, b)

Пример. Рассчитаем НОД для 28 и 64.

Как находим:

Распишем простые множители для каждого числа и подчеркнем одинаковые

Д (28) = 2 * 2 * 7

Д (64) = 2 * 2 * 2 * 2 * 2 * 2

Найдем произведение одинаковых простых множителей и запишем ответ

НОД (28; 64) = 2 * 2 = 4

Ответ: НОД (28; 64) = 4

Оформить поиск НОД можно в строчку, как мы сделали выше или в столбик, как на картинке.

Десятичные дроби

Существует еще один вид дробей, уверен ты его знаешь. Бери калькулятор и дели \( \displaystyle  11\) на \( \displaystyle  2\), например. Что пишет, \( \displaystyle  5,5\)? Что за штука такая?

Читается это как пять целых и пять десятых, равносильно \(\displaystyle5\frac{5}{10}\). Иными словами \( \displaystyle  11/2=5,5=5\frac{5}{10}\), все это одно и то же.

Дроби типа \( \displaystyle  5,5;\text{ }42,02;\text{ }0,122\) – все это десятичные дроби – это те же самые обыкновенные дроби, но в так называемой десятичной записи.

Десятичная запись используется для дробей со знаменателями \( \displaystyle  10\), \( \displaystyle  100\), \( \displaystyle  1000\) и т. д. В десятичных дробях так же есть целая и дробная части.

Для ясности возьмем вот такую дробь \( \displaystyle  12,856\):

• до запятой – целая часть (\( \displaystyle  12\));
• первый знак после запятой – десятые доли (\( \displaystyle  8/10\));
• второй – сотые доли (\( \displaystyle  5/100\));
• третий – (\( \displaystyle  6/1000\)).

Дроби на координатном луче

Все дробные числа, отвечающие обыкновенным дробям, имеют свое уникальное место на , то есть, существует взаимно однозначное соответствие между дробями и точками координатного луча.

Чтобы на координатном луче попасть в точку, соответствующую дроби m/n нужно от начала координат в положительном направлении отложить m отрезков, длина которых составляет 1/n долю единичного отрезка. Такие отрезки можно получить, разделив единичный отрезок на n равных частей, что всегда можно сделать с помощью циркуля и линейки.

Для примера покажем точку М на координатном луче, соответствующую дроби 14/10. Длина отрезка с концами в точке O и ближайшей к ней точке, отмеченной маленьким штрихом, составляет 1/10 долю единичного отрезка. Точка с координатой 14/10 удалена от начала координат на расстояние 14 таких отрезков.

Равным дробям отвечает одно и то же дробное число, то есть, равные дроби являются координатами одной и той же точки на координатном луче. Например, координатам 1/2, 2/4, 16/32, 55/110 на координатном луче соответствует одна точка, так как все записанные дроби равны (она расположена на расстоянии половины единичного отрезка, отложенного от начала отсчета в положительном направлении).

На горизонтальном и направленном вправо координатном луче точка, координатой которой является большая дробь, располагается правее точки, координатой которой является меньшая дробь. Аналогично, точка с меньшей координатой лежит левее точки с большей координатой.

Ответы на вопрос

Отвечает Хамитов Дамир.
15.10.2023 в 07:06

В расписании для студентов числитель и знаменатель обычно обозначают две разные половины учебного семестра. Номер недели будет зависеть от того, какая половина используется в данное время.
Числитель обычно относится к первой половине семестра, а знаменатель — ко второй половине. Это деление обусловлено организацией учебного процесса и может различаться в разных университетах или образовательных учреждениях.
Для студентов, имеющих числитель-знаменательную систему, в расписании указывается, какая неделя сейчас активна. Например, если указано «числитель», то это значит, что текущая неделя принадлежит к числителю, а студентам следует следовать расписанию, предназначенному для этой половины семестра. Наоборот, если указано «знаменатель», то это означает, что текущая неделя принадлежит к знаменателю.
Обычно, перед началом учебного семестра, студенты получают информацию о том, какая половина применяется в данный момент и как будут определяться номера недель. Эта информация может быть предоставлена учебным заведением или размещена на его веб-сайте.
Для удобства студентов, расписание может содержать указания о половине семестра, к которой относится каждая неделя. Это позволяет студентам планировать свою активность и посещать занятия в соответствии с правильной половиной семестра.

Действия с дробями

Сравнение дробей

Срaвнение дробей важно для понимания их величин относительно друг друга. Чтобы сравнить дроби, можно воспользоваться несколькими методами:. → Сравнeние дробей с одинаковым знаменателем: если дроби имеют одинаковый знаменатель, то сравнение производится по числителям

Например, для дробей 3/8 и ⅝ достаточно сравнить числители 3 и 5. Поскольку 5 больше 3, дробь 5/8 больше, чем 3/8​.→ Сравнениe дробей с разными знаменателями: в этом случае удобнее привести дроби к общему знаменателю. После приведения дробей к общему знаменателю сравнение осуществляется по числителям. Например, для дробей ⅖ и 3/7​:

→ Сравнeние дробей с одинаковым знаменателем: если дроби имеют одинаковый знаменатель, то сравнение производится по числителям. Например, для дробей 3/8 и ⅝ достаточно сравнить числители 3 и 5. Поскольку 5 больше 3, дробь 5/8 больше, чем 3/8​.→ Сравнениe дробей с разными знаменателями: в этом случае удобнее привести дроби к общему знаменателю. После приведения дробей к общему знаменателю сравнение осуществляется по числителям. Например, для дробей ⅖ и 3/7​:

1. Находим общий знаменатель: 35.
2. Приводим дроби к общему знаменателю: 

1. Сравниваем числители: 14 и 15. Следовательно, 3/7 больше, чем 2/5​.

Сокращение дробей

Сокращение дробей помогает упростить их вид и облегчить дальнейшие вычисления. Чтобы сократить дробь, нужно разделить числитель и знаменатель на их наибольший общий делитель (НОД).

Пример 1. Упростим дробь 18/24:

1. Находим НОД числителя и знаменателя. В данном случае НОД 18 и 24 равен 6.
2. Делим числитель и знаменатель на 6: 

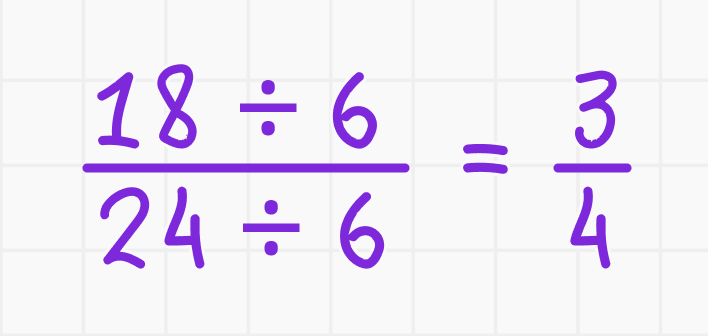
Пример 2. Упростим дробь 50/75​:

1. НОД числителя и знаменателя равен 25.
2. Делим числитель и знаменатель на 25: 

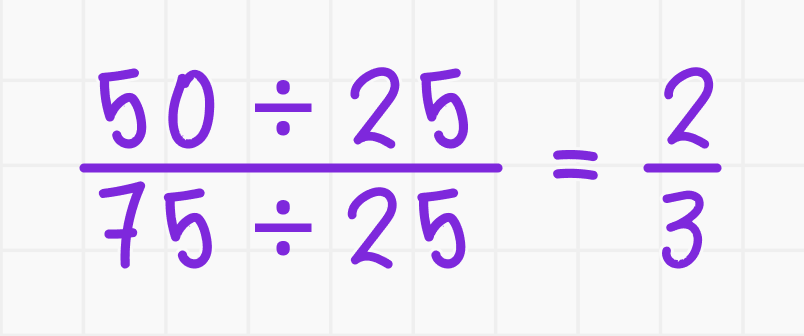
Сложение и вычитание дробей

Для сложения и вычитания дробей необходимо привести их к общему знаменателю, если он у них разный.

Сложение обыкновенных дробей:

Шаг 1. Найдите общий знаменатель дробей.

Шаг 2. Приведите дроби к общему знаменателю.

Шаг 3. Сложите числители дробей и оставьте общий знаменатель.

Пример:

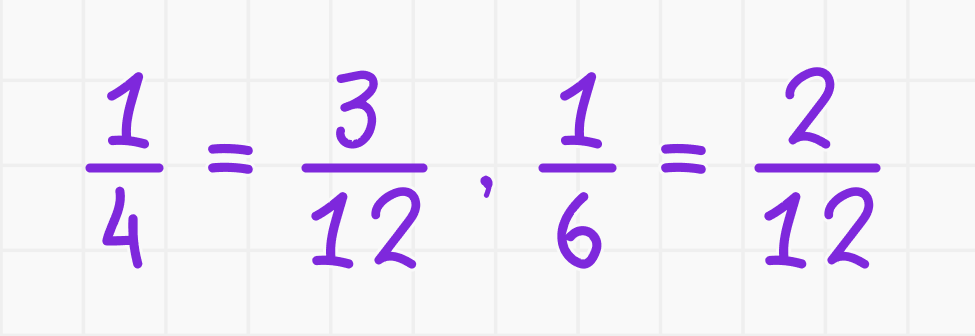
1. Общий знаменатель для 4 и 6 — 12.
2. Приводим дроби к общему знаменателю: 

1. Сложение:

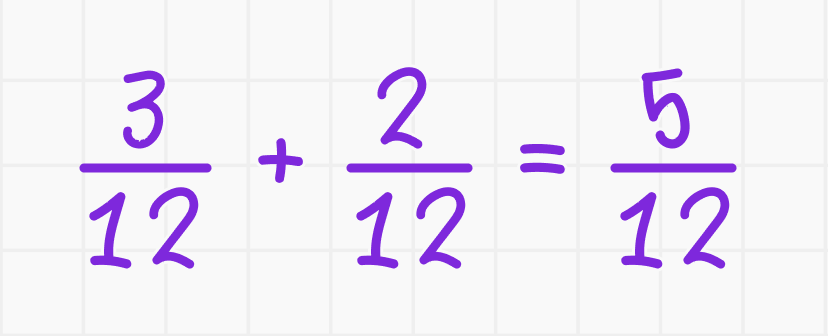
Вычитание обыкновенных дробей:

Шаг 1. Найдите общий знаменатель дробей.

Шаг 2. Приведите дроби к общему знаменателю.

Шаг 3. Вычтите числители дробей и оставьте общий знаменатель.

Пример: 

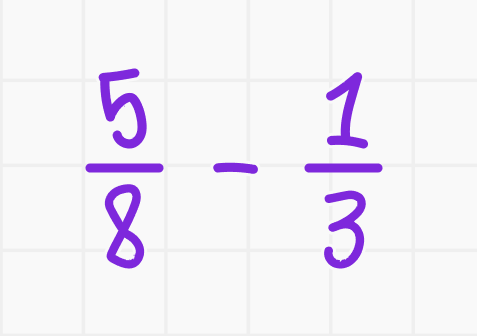
1. Общий знаменатель для 8 и 3 — 24.
2. Приводим дроби к общему знаменателю: 

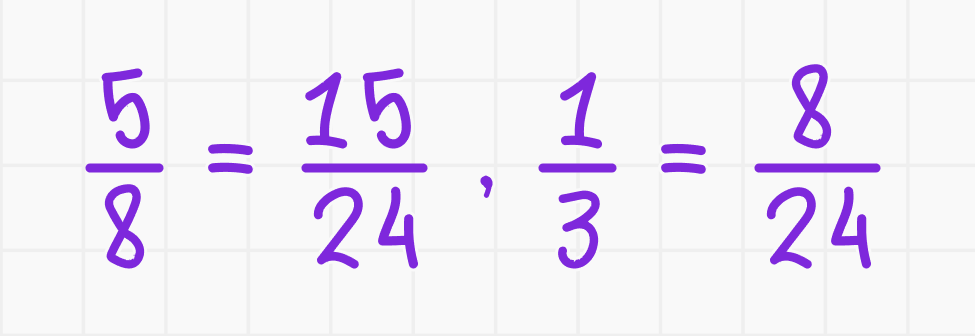
1. Вычитание: 

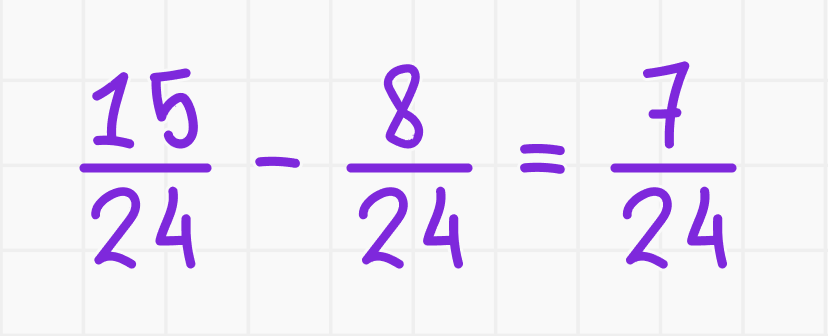
Умножение и деление дробей

Умножение обыкновенных дробей:

1. Умножьте числители дробей между собой.
2. Умножьте знаменатели дробей между собой.
3. Упростите дробь при необходимости.

Пример: 

1. Умножаем числители: 2 ∙ 3 = 6.
2. Умножаем знаменатели: 5 ∙ 4 = 20.
3. Результат:

упрощаем до 

Деление обыкновенных дробей:

1. Умножьте первую дробь на обратную вторую дробь (инвертируйте вторую дробь).
2. Упростите дробь при необходимости.

Пример: 

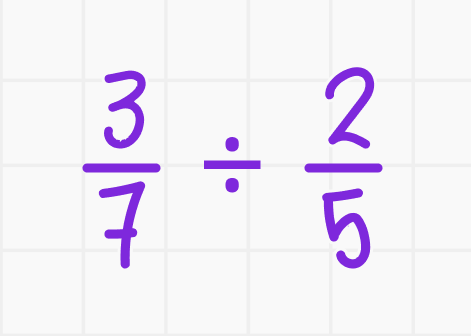
1. Переворачиваем вторую дробь:

1. Умножаем: 

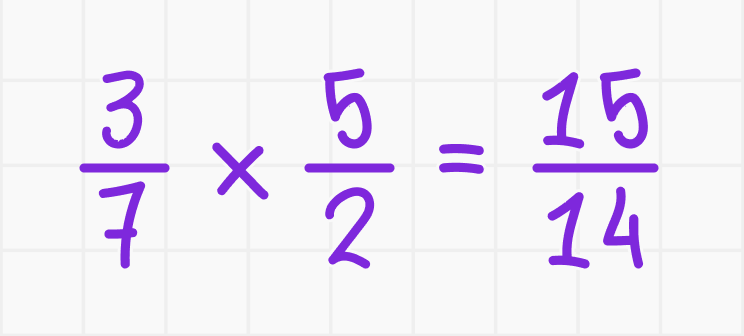
Определение обыкновенной дроби

Определение 1

Обыкновенные дроби используют для описания числа долей. Рассмотрим пример, с помощью которого можно дать определение обыкновенной дроби.

Яблоко разделили на $8$ долей. В этом случае каждая доля представляет одну восьмую долю целого яблока, т. е. $\frac{1}{8}$. Две доли обозначаются $\frac{2}{8}$, три доли — $\frac{3}{8}$ и т.д., а $8$ долей — $\frac{8}{8}$. Каждая из представленных записей называется обыкновенной дробью.

Приведем общее определение обыкновенной дроби.

Определение 2

Обыкновенной дробью называется запись вида $\frac{m}{n}$, где $m$ и $n$— любые натуральные числа.

Часто можно встретить следующую запись обыкновенной дроби: $m/n$.

Пример 1

Примеры обыкновенных дробей:

\[{3}/{4}, \frac{101}{345},\ \ {23}/{5}, \frac{15}{15}, {111}/{81}.\]

Замечание 1

Числа $\frac{\sqrt{2}}{3}$, $-\frac{13}{37}$, $\frac{4}{\frac{2}{7}}$, $\frac{2,4}{8,3}$ не являются обыкновенными дробями, т.к. не подходят под вышеприведенное определение.

Черта дроби как знак деления

Представление исходного предмета в виде n долей представляет собой не что иное как деление на n равных частей. После того как предмет разделен на n долей, мы его можем разделить поровну между n людьми – каждый получит по одной доле.

Если же у нас есть изначально m одинаковых предметов, каждый из которых разделен на n долей, то эти m предметов мы можем поровну разделить между n людьми, раздав каждому человеку по одной доле от каждого из m предметов. При этом у каждого человека будет m долей 1/n, а m долей 1/n дает обыкновенную дробь m/n. Таким образом, обыкновенную дробь m/n можно применять для обозначения деления m предметов между n людьми.

Так мы получили явную связь между обыкновенными дробями и делением (смотрите общее представление о делении натуральных чисел). Эта связь выражается в следующем: черту дроби можно понимать как знак деления, то есть, m/n=m:n.

С помощью обыкновенной дроби можно записать результат деления двух натуральных чисел, для которых не выполняется деление нацело. Например, результат деления 5 яблок на 8 человек можно записать как 5/8, то есть, каждому достанется пять восьмых долей яблока: 5:8=5/8.

Определение знаменателя в расписании: что это за понятие и смысл его использования

Знаменатель, в контексте расписания, представляет собой одну из двух основных составляющих этой структуры, вторую после числителя. Вместе эти два элемента определяют содержание и формат расписания, обеспечивая его полноту и структурированность.

Знаменатель обычно указывает на то, кто или что является объектом расписания или группой элементов, которые должны быть упорядочены в рамках одной временной единицы (например, дня, недели или месяца). Знаменатель может быть произвольным словом, символом, цифрой или фразой, которые имеют смысловую связь с содержанием расписания.

С помощью знаменателя можно определить, к какому конкретному типу заданий, событий или процессов относится каждая запись в расписании. Например, если расписание относится к учебным занятиям, знаменатель может указывать на название предмета или группу студентов. Если это расписание работы сотрудников, знаменатель может содержать информацию о подразделении или статусе сотрудника.

Важным аспектом использования знаменателя в расписании является его уникальность и ясность. Он должен быть понятным и легким для идентификации, чтобы пользователи могли быстро определить, к какой группе или заданию относится каждый элемент расписания. Кроме того, знаменатель помогает упорядочить и сортировать записи в расписании, что упрощает его использование и навигацию.

В итоге, знаменатель в расписании является важным элементом, который дополняет числитель и обеспечивает полноту и структурированность информации. Он помогает идентифицировать объекты или группы элементов расписания, упрощает его навигацию и облегчает взаимодействие пользователей с этой структурой.

Что значит числитель и знаменатель в расписании?

Что обозначает числитель и знаменатель в расписании для студентов?

Можно узнать в расписании недель, какой является неделя в учебном семестре – по числителю или по знаменателю. Что это значит? Как в этом разобраться?

В высших учебных заведения достаточно много предметов. Кафедры общественных наук (философия, история, политология и пр.) читают лекции и проводят семинары у всех студентов, учащихся в этом учебном заведении, вне зависимости от специальности. Опять же количество часов по разным предметам неодинаковое и их равномерное распределение на весь семестр достаточно сложный, трудоемкий и гибкий процесс. Поэтому в ВУЗах применяют двухнедельное расписание. В числителе стоит расписание на 1-ю неделю (нечетную), в знаменателе на 2-ю (четную).

Отчет недель начинается с 1 дня начала семестра. Часто на расписании указывают по какой неделе проходят занятия. Т.е. каждый понедельник меняют цифры 1 и 2.

Числитель и знаменатель в расписании.

Для тех, кто еще не сталкивался с таким видом расписания. Предмет, урок или пара, при таком расписании может в одну неделю быть, а в другую нет. Или в одну неделю один предмет в это время, а в другую неделю в это же время другой предмет.

Выглядит это следующим образом:

строчка в расписании делится на две строки (одна строка под другой или строки через косую линию), в каждой из которой написан разный предмет.

Верхний предмет, или числитель, обычно идет в четную неделю, а предмет в знаменателе, — в нечетную.

Вот простенький пример, как выглядит подобное расписание, и показано, где числитель, и где знаменатель:

Давайте разберем подробно, что значит «числитель» и «знаменатель» в расписании занятий для студентов в ВУЗах и других учебных заведениях.

Для начала стоит отметить то, что недели в учебном году имеют номер. Исчисление начинается с первого учебного дня. Это будет первой неделей, а дальше по нарастающей. Первая неделя — нечетная, вторая — четная. Дальше смотрим на номер недели и вспоминаем школьные знания. Если номер недели делится на два без остатка, значит неделя четная, если не делится, то нечетная. Нечетная неделя — это числитель, четная неделя — знаменатель.

Идем дальше. Расписание составляется на основе установленной образовательной программы. Каждый предмет имеет определенное количество часов для проведения семинаров и лекций. Возьмем два произвольных предмета: Предмет А и предмет Б. У предмета А количество академических часов солидно больше, чем у предмета Б. Поэтому методисты ставят пары по числителю и знаменателю, чтобы уместить все необходимые часы обучения. То есть идет предмет Б, но только по четной учебной неделе. На нечетной неделе он заменяется предметом А. В расписании это обычно выглядит как одна клетка для определенного дня, разделенная горизонтальной полосой. Сверху числитель(нечетная неделя), снизу знаменатель(четная неделя).

Вот наглядный пример числителя и знаменателя на примере расписания ВУЗа, в котором училась когда-то я:

1 — числитель, 2 — знаменатель. 10.45 — 12.20 — время проведения пар каждый четверг. По нечетным неделям(числителю) в четверг с 10.45 до 12.20 будет лекция по системам автоматизированного проектирования, по четным неделям(знаменателю) будет лекция по ядерным технологиям. Надеюсь, это я смогла доступно донести на примере.

Посмотреть, какая учебная неделя сейчас идет можно в еженедельном журнале посещения занятий. Они обычно всю неделю находятся у старосты и сдаются в деканат в конце недели. В журнале отмечается номер недели. Также эта информация есть на информационном стенде деканата факультета, а также Вашей кафедры.

Источник

1.2.1. document.write(‘Обыкновенные дроби’); window.top.document.title = «1.2.1. Обыкновенные дроби»;

Можно еще больше расширить числовое множество – так, чтобы операция деления над натуральными числами была выполнима всегда. Для этого введем понятие дроби.

Если n = 1, то дробь имеет вид
и её часто записывают просто m. Отсюда, в частности, следует, что любое натуральное число представимо в виде обыкновенной дроби со знаменателем 1.

Например,
так как
Из этого определения следует, что дробь
равна любой дроби вида
где m – натуральное число. В самом деле, так как
то   Итак, мы готовы сформулировать следующее правило.

С помощью основного свойства дроби можно заменить данную дробь другой дробью, равной данной, но с меньшими числителем и знаменателем. Такая замена называется сокращением дроби. Например,
(здесь числитель и знаменатель разделили сначала на 2, а потом ещё на 2). Сокращение дроби можно провести тогда и только тогда, когда её числитель и знаменатель не являются взаимно простыми числами. Если же числитель и знаменатель данной дроби взаимно просты, то дробь сократить нельзя, например,
– несократимая дробь.

Модель 1.5. Сокращение обыкновенных дробей

Справедливо следующее утверждение (его мы докажем ниже):

Из двух дробей с одинаковыми знаменателями больше та дробь, числитель которой больше. Например,
Из двух дробей с одинаковыми числителями больше та дробь, знаменатель которой меньше. Например,
Чтобы сравнить две дроби с разными числителями и знаменателями, нужно преобразовать обе дроби так, чтобы их знаменатели стали одинаковыми. Такое преобразование называется приведением дробей к общему знаменателю.

Модель 1.6. Сравнение обыкновенных дробей

Теперь знаменатели этих дробей одинаковы, значит,
Следовательно,
Ясно, что две дроби можно привести не к единственному общему знаменателю. Так, в нашем примере дроби  и 
можно привести к знаменателю 56. В самом деле:

наименьшему общему знаменателю
Пример 1

Привести дроби к наименьшему общему знаменателю:  и 

Решение

В рассмотренном примере числа 4 и 3 называют дополнительными множителями для первой и второй дроби соответственно.

Теперь мы можем определить арифметические действия с дробями.

Сложение. Если знаменатели дробей одинаковы, то чтобы сложить эти дроби, нужно сложить их числители; знаменатель остаётся прежним, то есть

Вычитание. Если две дроби имеют одинаковые знаменатели, то

Модель 1.7. Сложение и вычитание обыкновенных дробей

Умножение. Произведение двух дробей равно дроби, числитель которой равен произведению числителей данных дробей, а знаменатель равен произведению их знаменателей, то есть

Деление. Деление дробей осуществляют следующим образом:

В случае умножения и деления смешанных чисел всегда удобно переходить к неправильным дробям.

Модель 1.8. Умножение и деление обыкновенных дробей

Пример 2

Сложить две дроби
и
Ответ представить в виде неправильной дроби.

Показать решение

Пример 3

Сложить две дроби
и
Ответ представить в виде неправильной дроби.

Показать решение

Теперь можно показать, что любую неправильную дробь можно представить в виде суммы натурального числа и правильной дроби (или в виде натурального числа, если дробь
такова, что число m кратно n, например, ).

Пример 4

Представить неправильную дробь в виде суммы натурального числа и правильной дроби: 1)
2)

Показать решение

Всякую неправильную дробь можно представить в виде смешанного числа (или в виде натурального числа). Понятно также, что верно и обратное: всякое смешанное число может быть представлено в виде неправильной дроби. Например,

Пример 5

Выполнить действия.

Показать решение

Значение недели числитель и недели знаменатель для календарного планирования

В календарном планировании неделя числитель и неделя знаменатель используются для определения порядка и нумерации недель в году. Этот подход, который применяется в разных странах и областях, позволяет упорядочить и систематизировать рабочие и учебные процессы, а также планирование событий и мероприятий.

Неделя числитель — это неделя, которая имеет полный набор семи дней и начинается с первого января года. В этой системе первая неделя года всегда является неделей числителем и продолжается до окончания ее полного семидневного цикла. Вторая неделя тоже является числителем, третья — тоже, и так далее.

Неделя знаменатель — это неделя, которая начинается после окончания полного семидневного цикла первой недели года. То есть, если первая неделя года является числителем, то вторая неделя будет знаменателем. Далее, каждая четвертая неделя будет знаменателем, а каждая третья — числителем.

Проиллюстрируем это на примере:

Пример 1:

Допустим, первый января года является понедельником. В этом случае, первая неделя года будет неделей числителем и будет включать дни с понедельника по воскресенье. Затем, вторая неделя будет неделей знаменатель и будет включать дни с понедельника по воскресенье.

Неделя числитель: 1-7 января

Неделя знаменатель: 8-14 января

Пример 2:

Если первое января является субботой, то первая неделя года все равно будет объявлена неделей числителем и будет включать дни с субботы по пятницу следующей недели. Вторая неделя будет неделей знаменатель и будет включать дни с субботы по пятницу следующей недели.

Неделя числитель: 1-7 января

Неделя знаменатель: 8-14 января

Такой подход позволяет легко определить номер недели в году и использовать ее для планирования мероприятий, расписания учебных занятий, оформления рабочих графиков и других задач, связанных с календарной организацией.

Неправильные дроби. Выделение целой части

Если числитель меньше знаменателя, такая дробь называется правильной. В противном случае (т.е. когда числитель больше или хотя бы равен знаменателю) дробь называется неправильной, и в ней можно выделить целую часть.

Целая часть записывается крупным числом спереди перед дробью и выглядит так (отмечена красным):

Чтобы выделить целую часть в неправильной дроби, надо выполнить три простых шага:

1. Найдите, сколько раз знаменатель помещается в числителе. Другими словами, найдите максимальное целое число, которое при умножении на знаменатель все равно будет меньше числителя (в крайнем случае — равно). Это число и будет целой частью, поэтому записываем его спереди;
2. Умножьте знаменатель на целую часть, найденную в предыдущем шаге, а результат вычтите из числителя. Полученный «огрызок» называется остатком от деления, он всегда будет положительным (в крайнем случае — ноль). Записываем его в числитель новой дроби;
3. Знаменатель переписываем без изменений.

Ну как, сложно? На первый взгляд, может быть и сложно. Но стоит немного потренироваться — и вы будете делать это почти устно. А пока взгляните на примеры:

Во всех примерах целая часть выделена красным цветом, а остаток от деления — зеленым.

Обратите внимание на последнюю дробь, где остаток от деления оказался равным нулю. Получается, что числитель полностью разделился на знаменатель. Это вполне логично, ведь 24 : 6 = 4 — суровый факт из таблицы умножения

Это вполне логично, ведь 24 : 6 = 4 — суровый факт из таблицы умножения.

Если все делать правильно, числитель новой дроби обязательно будет меньше знаменателя, т.е. дробь станет правильной. Отмечу также, что лучше выделять целую часть в самом конце задачи, перед записью ответа. Иначе можно значительно усложнить вычисления.

Доли целого

Сначала введем понятие доли.

Предположим, что у нас есть некоторый предмет, составленный из нескольких абсолютно одинаковых (то есть, равных) частей. Для наглядности можно представить, например, яблоко, разрезанное на несколько равных частей, или апельсин, состоящий из нескольких равных долек. Каждую из этих равных частей, составляющих целый предмет, называют долей целого или просто долей.

Заметим, что доли бывают разные. Поясним это. Пусть у нас есть два яблока. Разрежем первое яблоко на две равные части, а второе – на 6 равных частей. Понятно, что доля первого яблока будет отличаться от доли второго яблока.

В зависимости от количества долей, составляющих целый предмет, эти доли имеют свои названия. Разберем названия долей. Если предмет составляют две доли, любая из них называется одна вторая доля целого предмета; если предмет составляют три доли, то любая из них называется одна третья доля, и так далее.

Одна вторая доля имеет специальное название – половина. Одна третья доля называется третью, а одна четверная доля – четвертью.

Для краткости записи были введены следующие обозначения долей. Одну вторую долю обозначают как или 1/2, одну третью долю – как или 1/3; одну четвертую долю – как или 1/4, и так далее. Отметим, что запись с горизонтальной чертой употребляется чаще. Для закрепления материала приведем еще один пример: запись обозначает одну сто шестьдесят седьмую долю целого.

Понятие доли естественным образом распространяется с предметов на величины. Например, одной из мер измерения длины является метр. Для измерения длин меньших, чем метр, можно использовать доли метра. Так можно воспользоваться, например, половиной метра или десятой или тысячной долей метра. Аналогично применяются доли других величин.

Что значит неделя числитель неделя знаменатель

Просто через неделю чередуется расписание, наверное так Часы удобнее распределять. На первой неделе верхнее расписание, на второй нижнее, потом верхнее, потом нижнее и так далее Это не значит, что нижняя/верхняя будет всегда легче, они могут быть одинаково убогими

Смотри на примере по фото: допустим Группа «перан-92»Несмотря на то, что у всех других групп в этот день есть первая пара, у них никогда ее нет. В этот день на любой неделе они приходят ко второй паре. Далее у них:Показать полностью. — на верхней неделе практикум по коммуникации, практика речи и культурные коды, то есть 3 пары— на нижней неделе практикум по коммуникации, практика речи и ВСЕ. Кодов нет! Они только на верхней неделе, значит 2 пары

Не суди по тому, что только четыре дня, бывает и так. Значит повезло и нагрузка так распределилась, что этот день свободен

Про чёрные пары не могу сказать, что это значит, у меня такого не было

Источник