Количественный смысл натуральных чисел
Натуральные числа используются для чего-то, что можно посчитать или пронумеровать. Например, мы можем посчитать, сколько ножек у стола, сколько учеников в классе или даже сколько орешков в пачке.
А ещё мы можем пронумеровать автобусные маршруты, билеты на спектакль или спортивные разряды.
Сколько человек в классе? 25. Это значит, что именно столько человек должны присутствовать на уроке (если, конечно, никто не болеет).
Какой номер маршрута у автобуса? 17-й. Это значит, что в городе есть ещё как минимум шестнадцать разных маршрутов, по которым ходят автобусы.
Натуральные числа здесь выступают как средство для нумерации. Именно в этом заключается их количественный смысл — обозначать количество того, что можно посчитать.
Действия с десятичными дробями
Десятичные дроби – это обычные числа. Мы можем складывать их, вычитать из одной другую, умножать и делить.
Очень важно уметь правильно производить с ними математические действия, так как зачастую именно от арифметических ошибок зависит твоя оценка на экзамене. Несомненно, ты знаешь, как все это делать, но на всякий случай, дам тебе краткую инструкцию к применению
Несомненно, ты знаешь, как все это делать, но на всякий случай, дам тебе краткую инструкцию к применению.
Как складывать десятичные дроби
При сложении десятичные дроби записываются «столбиком», так чтобы одноимённые разряды находились друг под другом без смещения. Соответственно, запятые стоят четко друг под другом.
Разберемся на примере:
Сложение происходит, как и сложение натуральных чисел в столбик, при этом запятая в ответе ставится четко на том же месте, как и в складываемых числах.
Если исходные числа имеют разное количество знаков после запятой, то к дроби с меньшим количеством десятичных знаков нужно приписать необходимое число нулей, чтобы уравнять в дробях количество знаков после запятой.
Если при сложении в сумме мы получаем больше \( 10\), то одна единица прибавляется к сумме при сложении цифр следующего разряда.
Решим наш пример, учтя все правила:
Разобрался? Посчитай в столбик самостоятельно:
- \( 0,0125+0,141\)
- \( 2,4225+0,34\)
- \( 122,4355+1,34\)
- \( 2,435+12,3\)
Сравним ответы:
- \( 0,0125+0,141=0,1535\)
- \( 2,4225+0,34=2,7625\)
- \( 122,4355+1,34=123,7755\)
- \( 2,435+12,3=14,735\)
История числа «пятьдесят»
Впервые число «пятьдесят» появилось в древнеримской системе счета и обозначается символом «L». В римской системе счета числа образовываются из сочетания следующих символов: I, V, X, L, C, D и M.
В дополнение к древнеримскому использованию числа «пятьдесят», оно также имеет важное значение в современной математике. В системе десятичных чисел число «пятьдесят» может быть представлено цифрой «5» с последующим символом «0», чтобы указать его позицию. Число «пятьдесят» также часто используется для обозначения половину ста или половину отклонения от некоторого нормального значения
Например, в фармацевтической области, «пятьдесят» может означать 50% активного ингредиента в лекарственном препарате
Число «пятьдесят» также часто используется для обозначения половину ста или половину отклонения от некоторого нормального значения. Например, в фармацевтической области, «пятьдесят» может означать 50% активного ингредиента в лекарственном препарате.
Во многих культурах число «пятьдесят» имеет своя символическая значимость. Оно может отражать силу и стабильность, а также символизировать середину или баланс между двумя крайностями.
Многозначные числа в математике
Прежде чем перейти к основному понятию, требуется вспомнить о натуральных числах – тех, что используются при счете.
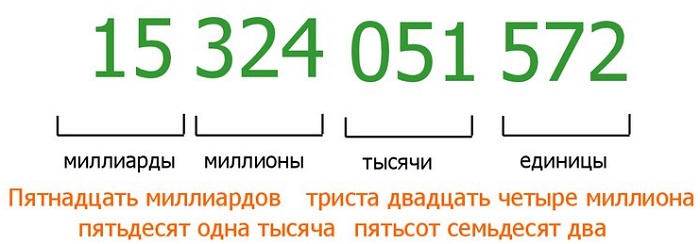
Их особенность в том, что они имеют наименьшее значение (1), но не имеют наибольшего или конечного. Ведь счет не имеет конца.
Их можно разделить на группы, в зависимости от того, сколько символов входит в их состав:
-
Однозначные – если для отображения требуется один символ (1, 2, 3 и т. д.).
-
Двузначные – когда для записи нужно две цифры (10, 11, 12 и т. д.).
-
Трехзначные – записывают с помощью трех символов (100, 101, 102 и т. д.).
Перечисление можно продолжать дальше – четырехзначные, пятизначные и т. д. Но для простоты обозначения все числа, содержащие в своей структуре более 1 цифры, называют многозначными.
Определение и смысл
Десятковая система счисления является одной из наиболее распространенных систем счисления и широко используется в повседневной жизни. Она основана на позиционной записи чисел, где каждая позиция имеет вес, равный степени десяти. Таким образом, каждая цифра в числе может быть умножена на соответствующую степень десяти и затем сложена для получения значения числа в десятичной системе.
Примеры чисел, представленных в 10 десятках:
- 10 — это число, которое состоит из одного десятка;
- 20 — это число, которое состоит из двух десятков;
- 50 — это число, которое состоит из пяти десятков;
- 100 — это число, которое состоит из десяти десятков;
- 1000 — это число, которое состоит из ста десятков.
10 десятков играют важную роль в математике, науке и повседневной жизни. Они используются для счета, измерений, финансовых расчетов и т. д. Понимание и использование 10 десятков является важным навыком, который помогает в повседневной жизни и профессиональной деятельности.
Объяснение принципа
Когда мы используем десятичную систему, каждая цифра в числе имеет свое значение в зависимости от позиции, в которой она находится. Например, число 1234 состоит из цифр 1, 2, 3 и 4. Значение каждой цифры в числе определено позицией, которую она занимает. В этом случае, цифра 1 находится в позиции тысяч, цифра 2 — в позиции сотен, цифра 3 — в позиции десятков и цифра 4 — в позиции единиц. Таким образом, число 1234 можно интерпретировать как 1 тысяча + 2 сотни + 3 десятки + 4 единицы.
Чтобы получить число в десятичной системе из числа, записанного в другой системе счисления, необходимо умножить каждую цифру числа на некоторую степень основания системы счисления, а затем сложить полученные произведения. Например, число 101 в двоичной системе счисления можно перевести в десятичную систему следующим образом: (1 * 2^2) + (0 * 2^1) + (1 * 2^0) = 5.
10-ая система счисления широко используется в математике, физике, финансах и других областях науки и жизни. Понимание основ 10-ой системы счисления и способности использовать ее позволяют нам легко манипулировать числами и выполнять арифметические операции, а также понимать их значения и взаимосвязи.
Практическое значение
10 десятков объяснение имеет практическое значение в различных сферах деятельности.
В математике этот термин используется для представления чисел в десятичной системе счисления. Благодаря 10 десяткам можно легко выполнять арифметические операции и проводить расчеты.
В экономике этот термин используется для обозначения единицы валюты. Например, в некоторых странах 10 десятков может означать 10 долларов или 10 евро. Использование этой системы позволяет упростить проведение финансовых операций и упростить конвертацию валют.
10 десятков также имеют практическое значение в ежедневной жизни. Они позволяют ориентироваться во времени, например, в 24-часовом формате времени. Также эта система используется для измерения длины (10 сантиметров), массы (10 граммов) и других физических величин.
Примеры использования 10 десятков находятся повсюду в различных аспектах нашей жизни, облегчая математические расчеты, финансовые операции и измерения различных величин.
Особенности числового выражения «пятьдесят десятков»
Числовое выражение «пятьдесят десятков» можно интерпретировать буквально как «50 раз десяток». Такое значение может являться преувеличением или метафорой, не имеющей точного аналога в реальности.
Примеры использования выражения «пятьдесят десятков» могут быть следующими:
1. Странные предложения
«Он сказал пятьдесят десятков, прежде чем понял, что никто не понимает, о чем он говорит.»
В этом примере выражение «пятьдесят десятков» указывает на нелепость и несуразность сказанного человека. Это выражение используется, чтобы подчеркнуть степень абсурдности или непонятности высказывания.
2. Большое количество
«Она принесла пятьдесят десятков пирогов на вечеринку.»
В данном примере выражение «пятьдесят десятков» указывает на большое количество пирогов. Оно может быть использовано для усиления эффекта ощущения изобилия и излишества.
3. Необычное действие
«Они покрыли стены комнаты пятьдесят десятков разноцветной краской.»
В этом примере выражение «пятьдесят десятков» указывает на нестандартный и необычный подход к окрашиванию стен. Оно используется для представления эксцентричности и оригинальности действия.
Таким образом, выражение «пятьдесят десятков» имеет своеобразное значение и часто используется с иронией. Оно позволяет выразить большое количество, странность или необычность событий или предметов.
Что такое натуральное число
Слово «натуральный» обозначает природный, естественный. То есть, натуральное число — это число, которое получается естественным образом при подсчёте чего-либо.
Ноль не является натуральным числом, ведь ноль — это пустота, нисколько предметов.
Отрицательные числа, перед которыми стоит знак минуса, такие как -1, -19, -327, не являются натуральными, потому что они обозначают то, чего не хватает. Следовательно, их нельзя посчитать.
Нецелые числа, те, которые обозначают половину, треть, четверть и тому подобное, тоже не относятся к натуральным.
Самое маленькое натуральное число — 1.
Натуральных чисел бесконечно много, потому что, если представить себе самое-самое большое натуральное число, то всё равно к нему можно прибавить 1, и получится ещё большее число. Бесконечность натуральных чисел обозначается латинской буквой N.
Практика:
Попросите ребёнка посмотреть вокруг себя и сосчитать, сколько он видит книг, сколько тетрадок и сколько ручек.
Например, 8 книг, 2 тетради и 1 ручка.
8, 2 и 1 — это натуральные числа. Они обозначаются такими же цифрами: 8, 2 и 1.
Числа от 1 до 100. Состав числа. Круглые числа
Предыдущее число — то число, которое при счете следует перед данным числом.
56 , 57
Последующее число — то число, которое при счете называют сразу после данного числа.
56, 57
Однозначные и двузначные числа
Вспомни, что каждая цифра в записи занимает определенное место.
Единицы стоят на первом месте справа.
Десятки стоят на втором месте справа.
Однозначные числа записываются ОДНОЙ цифрой: 5, 9, 2, 5.
Двузначные числа записываются ДВУМЯ цифрами: 54, 91, 42, 85.
Самое маленькое однозначное число — .
Самое большое однозначное число — 9.
Самое маленькое двузначное число — 10.
Самое большое двузначное число — 99.
Всего на рисунке 35 палочкек.
35 = 30 + 5
Состав числа 35 — 3 дес. 5 ед.
Красных палочек 12.
12 = 10 + 2
Состав числа 12 — 1 дес. 2 ед.
Синих палочек всего 23.
23 = 2 дес. 3 ед.
23 = 20 + 3
Состав числа 23 — 2 дес. 3 ед.


Теперь научимся представлять числа в виде суммы разрядных слагаемых.
Какие разряды выделяют в двузначных числах?
В двузначных числах выделяют разряд десятков и разряд единиц, то есть двузначное число можно представить следующим образом:
десятки + единицы
В числе 35 три десятка и 9 единиц:
Сравнение двузначных чисел
Числа 42 и 24 похожи тем, что в их записи использованы одинаковые цифры: цифра 4 и цифра 2. Но цифра 4 для числа 42 означает десятки, а для 24 — единицы, цифра 2 для числа 42 означает единицы, а для 24 — десятки.
| Число | 42 | 24 |
| Количество десятков | 4 | 2 |
| Количество единиц | 2 | 4 |
1. Сравнение двузначных чисел всегда начинается с десятков.
2. Если количество десятков одинаково, тогда переходят к сравнению единиц.
Круглые числа
Числа, которые оканчиваются на 0, называются круглыми. — 60, 30, 20.
В разряде единиц у круглого числа — число 0. — 70, 90, 40.
10, 20, 30, 40, 50, 60, 70, 80, 90, 100.
1 дес. + 4 дес. = 5 дес.
5 дес. = 50, значит,
10 + 40 = 50
Десять любых предметов можно назвать – ОДИН ДЕСЯТОК.

Десятками можно считать:
— это 2 десятка — записываю так: 2 дес.
Действия с десятками и единицами
— это 31
Как решить пример 34 + 25?
34 — это 3 дес. и 4 ед.
25 — это 2 дес. и 5 ед.
3 дес. и 4 ед. + 2 дес. и 5 ед. = 5 дес. 9 ед.
Можно записать короче:
Число 34 представляю в виде суммы разрядных слагаемых: 30 и 4, число 25 тоже представляю как 20 и 5. Теперь начинаю вычислять:
Сначала складываю единицы:
Теперь складываю десятки:
Запись решения выглядит так:
34 + 25 = (30 + 20) + (4 + 5) = 50 + 9 = 59
Десятки складываются с десятками.
Единицы складываются с единицами.

Как решить пример 38 — 16?
Число 38 — можно представить как 3 дес. и 8 ед.
Число 16 — это 1 дес. 6 ед.
3 дес. 8 ед. — 1 дес. 6 ед. = 2 дес. 2 ед.
38 — 16 = (30 — 10) + (8 — 6) = 20 + 2 = 22
Можно рассуждать так:
Число 38 представим в виде суммы разрядных слагаемых 30 и 8, а число 16 представим так: 10 и 6. Удобно число 6 вычесть из числа 8, получим 2. Затем число 10 вычтем из числа 30, получим 20. Теперь 2 прибавим к числу 20. Получим 22.
38 — 16 = 22
Десятки вычитаются из десятков.
Единицы вычитаются из единиц.

Мы рассмотрели случаи устных вычислений с двузначными числами.
Познакомиться с письменными приема вычислений (сложением в столбик и вычитанием в столбик) можно в нашем справочнике.
Что такое единицы?
В математике единицы – это числа от 1 до 9, которые используются для обозначения одного объекта или единицы измерения. Они являются базовыми компонентами числовой системы и служат для формирования всех остальных чисел.
Единицы представляют собой первый разряд числа. Например, в числе 352 первая цифра 3 является сотнями, вторая цифра 5 – десятками, а последняя цифра 2 – единицами.
Чтобы лучше понять, как работают единицы, рассмотрим примеры:
- Если имеется число 735, то в нем 7 – это количество сотен, 3 – количество десятков, и 5 – количество единиц.
- В числе 246, первая цифра 2 – количество сотен, вторая цифра 4 – количество десятков и третья цифра 6 – количество единиц.
Для удобства чтения больших чисел часто используется запятая или пробел для разделения разрядов. Например, число 1 000 000 может быть записано как 1,000,000.
Единицы играют важную роль в математике, так как с их помощью можно обозначать количество или размер объектов, а также выполнять различные операции, такие как сложение, вычитание, умножение и деление.
Что такое множество в математике и как оно обозначается
Множество – это количество предметов или чисел, обладающих общими свойствами.

Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.
В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A1, A2 и т. д.
Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a1, a2 и т. д.
Границы совокупности обозначаются фигурными скобками { }.
Пример:
- А = {а, в, с, у} – А состоит из четырех элементов.
- Записать совокупность Z согласных букв в слове «калькулятор»:
Z = {к, л, т, р}, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.
Принадлежность элементов множеству обозначается знаком – Є.
Пример: N = {a, b, c, y}, а Є N – элемент «а» принадлежит N.
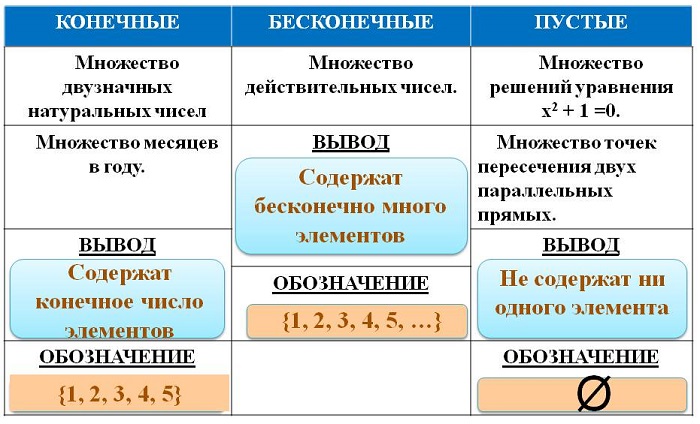
Выделяют три вида множеств:
- конечные — совокупности, имеющие максимальный и минимальный предел (например, отрезок);
- бесконечные — не являющиеся конечными (например, числовые);
- пустые (обозначаются Ø) – не имеющие элементов.
Если две разные совокупности содержат одинаковые элементы, то одна из них (со всеми своими элементами) является подмножеством другой и обозначается знаком — ⊆.
Пример: А = {а, в, с, у} и В = {а, в, с, е, к} – все элементы А являются элементами совокупности В, следовательно А ⊆ В.
Если множества состоят из одинаковых элементов, их называют равными.
Пример: А = {23, 29, 48} и В = {23, 29, 48}, тогда А = В.
В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.
Обозначения
Множество чаще всего обозначают заглавными буквами латинского алфавита, а его элементы — строчными. При этом элементы заключаются в фигурные скобки.
Например, если наших друзей зовут Том, Джон и Лео, то мы можем задать множество друзей, элементами которого будут Том, Джон и Лео.
Обозначим множество наших друзей через заглавную латинскую букву F (friends), затем поставим знак равенства и в фигурных скобках перечислим наших друзей:
F = { Том, Джон, Лео }
Пример 2. Запишем множество делителей числа 6.
Обозначим через любую заглавную латинскую букву данное множество, например, через букву D
D
затем поставим знак равенства и в фигурных скобках перечислим элементы данного множества, то есть перечислим делители числа 6
D = { 1, 2, 3, 6 }
Если какой-то элемент принадлежит заданному множеству, то эта принадлежность указывается с помощью знака принадлежности ∈. К примеру, делитель 2 принадлежит множеству делителей числа 6 (множеству D). Записывается это так:
2 ∈ D
Читается как «2 принадлежит множеству делителей числа 6»
Если какой-то элемент не принадлежит заданному множеству, то эта не принадлежность указывается с помощью зачёркнутого знака принадлежности ∉. К примеру, делитель 5 не принадлежит множеству D. Записывается это так:
5 ∉ D
Читается как «5 не принадлежит множеству делителей числа 6»
Кроме того, множество можно записывать прямым перечислением элементов, без заглавных букв. Это может быть удобным, если множество состоит из небольшого количества элементов. Например, зададим множество из одного элемента. Пусть этим элементом будет наш друг Том:
{ Том }
Зададим множество, которое состоит из одного числа 2
{ 2 }
Зададим множество, которое состоит из двух чисел: 2 и 5
{ 2, 5 }
Множество натуральных чисел
К совокупности натуральных чисел (N) относятся цифры, используемые при счете — от 1 до бесконечности.

Натуральные числа используют для исчисления порядка предметов. Обязательное условие данной числовой группы — каждое следующее число больше предыдущего на единицу.
N = {9, 11, 13, 15……}.
Относится ли ноль к натуральным числам? Это до сих пор открытый вопрос для математиков всего мира.
Множество целых чисел
Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль:
Z = {-112, -60, -25, 0, 36, 58, 256}.
Следовательно, N — подмножество Z, что можно записать как N ⊆ Z. Любое натуральное число можно назвать так же и целым.
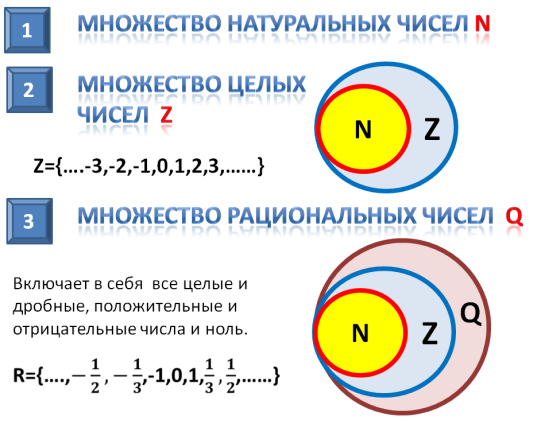
Множество рациональных чисел
Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел:
Q={-½; 0; ½, 5; 10}.
Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное:
5 = 5/1 = 10/2 = 25/5;
0,45 = 45/100 = 9/20.
Следовательно, N и Z являются подмножествами Q.
Десятичные дроби — коротко о главном
1. Определение
2. Конечная и бесконечная десятичная дробь
Десятичная дробь может быть:
- конечной, если она содержит конечное число цифр после запятой (\( \displaystyle \frac{8}{10},\ \frac{13}{100},\frac{49}{1000}\));
- бесконечной, в том числе периодичной, если конечное число цифр определить не определено (\( 0,05882352941…\));
- периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр (\( \displaystyle \frac{1}{7}=0,\underbrace{142857}_{{период}}\underbrace{142857}_{период}142…=0,\left( 142857 \right)\))
3. Свойства десятичных дробей
- Десятичная дробь не меняется, если справа добавить нули \( \displaystyle \frac{3}{100}=0,03=0,030=0,030000\)и т.д.;
- Десятичная дробь не меняется, если удалить нули, расположенные в конце десятичной дроби: \( 0,014330000=0,01433\);
- Десятичная дробь возрастает в \( 10\), \( 100\), \( 1000\) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций вправо: \( 0,0125\cdot 100=1,25\) (перенесли запятую на \( 2\) знака вправо – умножили на \( 100\) и дробь возросла в \( 100\) раз);
- Десятичная дробь уменьшается в \( 10\), \( 100\), \( 1000\) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций влево: \( 124,56:100=1,2456\) (перенесли запятую на \( 2\) знака влево – разделили на \( 100\) и дробь уменьшилась в \( 100\) раз).
4. Сложение десятичных дробей
Сложение происходит, как и сложение натуральных чисел в столбик, при этом запятая в ответе ставиться четко на том же месте, как и в складываемых числах.
5. Вычитание десятичных дробей
Так же, как и при сложении, при вычитании десятичные дроби записываются «столбиком»:
6. Умножение десятичных дробей
Десятичные дроби также записываются в столбик и умножаются как обыкновенные числа
При умножении нам неважно, стоят ли запятые под запятыми и так далее
Однако, удобно, когда числа выровнены по правому краю – умножение происходит более упорядочено.
7. Деление десятичных дробей
Деление десятичной дроби на натуральное число
- Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимания на запятую в делимом (то число, которое мы делим на какое-либо другое число)
- Ставим в частном запятую, когда заканчивается деление целой части делимого.
Деление десятичных дробей друг на друга
Что такое число «800»?
Число 800 может быть интерпретировано в разных контекстах. В математике оно может использоваться в качестве значения или меры величин, а в обыденной жизни — для описания количества или размера чего-либо.
Например, число 800 может означать:
- 800 рублей — сумма денег;
- 800 страниц — количество страниц в книге;
- 800 километров — расстояние между двумя городами;
- 800 лет — возраст какого-либо исторического события или периода;
Кроме того, число 800 может использоваться в выражениях или пословицах для усиления или уточнения.
Таким образом, число 800 имеет различные значения и может быть интерпретировано в зависимости от контекста, в котором оно используется.
Операции над множествами
Точно так же, как и все математические объекты, множества можно складывать и вычитать, то есть совершать операции.
Если две группы образуют третью, содержащую элементы исходных совокупностей – это называется суммой (объединением) множеств и обозначается знаком ∪.
Пример: В = {1, 6, 17} и С = {2, 13, 18}, В ∪ С= {1, 2, 6, 13, 17, 18}.
Если две группы совокупностей образуют третью, состоящую только из общих элементов заданных составляющих, это называется произведением (пересечением) множеств, обозначается значком ∩.
Пример: В = {36, 42, 53, 64} и С = {32, 42, 55, 66}, В ∩ С = {42}.
Если две совокупности образуют третью, включающую элементы одной из заданных групп и не содержащую элементы второй, получается разность (дополнение) совокупностей, обозначается значком /.
Пример: В = {12, 14, 16, 18} и С = {13, 14, 15, 17}, В / С = {14}.
В случае, когда В / С = С / В, получается симметричная разность и обозначается значком Δ.
Для «чайников» или кому трудно даётся данная тема операции с совокупностями можно отобразить с помощью диаграмм Венна:
Дополнение
С помощью данных диаграмм можно разобраться с законами де Моргана по поводу логической интерпретации операций над множествами.
Определение взаимно простых чисел
Сначала определимся, что значит простое число.
Главное свойство простых чисел в том, что простое число делится только на единицу и на само себя.
Таких чисел немного, большинство все-таки можно разделить на другие числа
В простых числах самое важное — это деление нацело. Дробные частные и деление с остатком не рассматриваем
Понятие взаимно простых чисел можно применить для двух целых чисел или для большего количества. Сформулируем, какие числа называются взаимно простыми.
Взаимно простые числа
Два целых числа a и b называются взаимно простыми, если их наибольший общий делитель равен единице — то есть НОД (a, b) = 1.
Проще говоря, взаимно простые числа — это целые числа, у которых нет общих делителей, кроме единицы.
Наибольшим общим делителем двух чисел a и b называется наибольшее число, на которое a и b делятся без остатка. Для записи может использоваться аббревиатура НОД. Для двух чисел можно записать так: НОД (a, b).
Наибольший общий делитель взаимно простых чисел — это единица, что следует из определения взаимно простых чисел.
Приведем примеры взаимно простых чисел.
Заметим, что два простых числа всегда являются взаимно простыми. Однако, два числа не обязательно должны быть простыми, чтобы быть взаимно простыми. Вот такая математика в 5 классе. И еще раз: либо одно из них, либо они оба могут быть составными и при этом являться взаимно простыми. Приведем пример.
Делители 8: ±1, ±2, ±4, ±8.
На математике в 5 и 6 класса часто встречаются задания, в которых нужно доказать, что конкретные целые числа являются взаимно простыми. Из чего обычно состоит такое доказательство:
Перед вычислением НОД можно заглянуть в таблицу простых чисел и проверить, вдруг исходные целые числа можно назвать простыми. Тогда решение будет проще, так как мы знаем, что НОД простых чисел равен единице.
Повторим еще раз. Что значит взаимно простые числа? Это целые числа, у которых нет общих делителей, кроме единицы.
Пример 1
Доказать, что числа 84 и 275 являются взаимно простыми.
Сверяемся с таблицей простых чисел. 84 и 275 не являются простыми, поэтому нельзя сразу сказать об их взаимной простоте.
Вычислим НОД. Используем алгоритм Евклида для нахождения НОД:
Доказали, что числа 84 и 275 взаимно простые.
Определение взаимно простых чисел можно расширить для трех и большего количества чисел.
То есть если у некоторого набора целых чисел есть положительный общий делитель, отличный от единицы, то эти целые числа не являются взаимно простыми.
Любая совокупность простых чисел составляет набор взаимно простых чисел, например, 2, 3, 11, 19, 151, 293 и 677 — взаимно простые числа. А четыре числа 12, −9, 900 и −72 не являются взаимно простыми, так как у них есть положительный общий делитель 3. Числа 17, 85 и 187 тоже не взаимно простые, потому что каждое из них можно разделить на 17.
Как определить взаимно простые числа:
Пример 2
Являются ли числа 331, 463 и 733 взаимно простыми?
Заглянем в таблицу простых чисел. Видим, что 331, 463 и 733 — простые. Значит, у них есть единственный положительный общий делитель — единица. Поэтому, 331, 463 и 733 есть взаимно простые числа.
Пример 3
Доказать, что числа −14, 105, −2 107 и −91 не являются взаимно простыми.
Найдем НОД заданных чисел и убедимся, что он не равен единице.
Делители целых отрицательных чисел совпадают с делителями соответствующих противоположных чисел. Поэтому НОД (−14, 105, 2 107, −91) = НОД (14, 105, 2 107, 91). Посчитаем:
НОД (14, 105, 2 107, 91) = 7.
Мы получили, что наибольший общий делитель исходных чисел равен семи, поэтому эти числа не являются взаимно простыми. Доказали.
Что значит выражение «50 десятков будьте добры»: объяснение и смысл
Оригинальное значение этого выражения связано с торговлей и употреблялось продавцами при продаже товаров, измеряемых в десятках. Если покупатель просил 50 десятков, то это означало, что он хотел приобрести 500 единиц товара. Продавцы использовали фразу «50 десятков будьте добры» для подчеркивания объема продажи и привлечения внимания покупателей.
В современном понимании выражение «50 десятков будьте добры» используется с иронией и сарказмом. Оно часто применяется для подчеркивания желания получить что-то ценное или дорогое, но необязательно играет роль настоящей просьбы о передаче денег или товара.
В целом, выражение «50 десятков будьте добры» является частью нашей культурной лексики и шутливо отсылает к прошлым временам торговли. Используется оно для создания легкой и спокойной обстановки в разговоре и подчеркивания смеха и шутки.
| Термин | Значение |
|---|---|
| Выражение | Фраза, передающая особое значение или смысл |
| Торговля | Процесс купли-продажи товаров или услуг |
| Ирония | Способ передачи значения, противоположного прямому смыслу слов |
| Сарказм | Остроумное и язвительное высказывание, использующее иронию |
| Культурная лексика | Словарный запас, связанный с культурой и историей определенного сообщества |
Десятичная система счисления
Для записи чисел в математике используется десятичная позиционная система счисления. В этой системе применяются $10$ цифр:
Рисунок $1$ Современные цифры и их «предки»
числа и цифры
Важно не путать числа с цифрами. Чисел бесконечно много, цифр — $10$. интересный факт
интересный факт
Сначала люди записывали цифры черточками и точками. Позднее изобрели римские цифры ($1 — I, 2 — II, 3 — III$ и т. д.). На Востоке была изобретена десятичная система счисления, пришедшая в Европу в Средние века.
{«questions»:,»explanations»:,»answer»:}}}]}. позиционная система счисления
позиционная система счисления
Разберем число $\textcolor{blue}{9}\textcolor{coral}{9}\textcolor{orange}{9}$. Оно состоит из трех одинаковых цифр, но позиция этих цифр отличается, по этому принципу меняется и разряд. Первая справа цифра — $\textcolor{orange}{девять \space единиц}$,цифра посередине — $\textcolor{coral}{девять \space десятков}$,цифра слева — $\textcolor{blue}{девять \space сотен}$.
Значение цифры зависит от ее позиции, десятичную систему счисления традиционно называют позиционной.
пример
В числе $555$ первая справа цифра означает $5$ единиц, вторая $5$ означает $5$ десятков, а третья — $5$ сотен.
Число $10$
$10$ единиц образует десяток, $10$ десятков образует сотню, $10$ сотен — тысячу:
- $1$ — единица;
- $10$ — десять;
- $100$ — сто;
- $1000$ — тысяча;
- $10\space000$ — десять тысяч;
- $100\space 000$ — сто тысяч;
- $1 \space000\space 000$ — миллион;
- $10 \space000\space 000$ — десять миллионов;
- $100 \space000\space 000$ — сто миллионов;
- $1 \space000\space 000\space 000$ — миллиард;
- $10\space 000\space 000\space 000$ — десять миллиардов и т. д.
Интерактив
Изменяйте цифру разряда, чтобы получить новое число.
digits
{"questions":,"answer":0}},"explanation":"В десятичной системе значение цифры зависит от ее позиции в числе. Если переставить цифры, получится другое число. Например, $54$ не равно $45$."}]}
Разрядные слагаемые
разрядные слагаемые
Образавр покупал ткань для штор. Он попросил продавца отрезать ему $\textcolor{blue}{3}$ метра ткани, но потом решил добавить еще $\textcolor{orange}{50}$ сантиметров, а затем — еще $\textcolor{green}{4}$ сантиметра.
Посчитаем длину получившихся штор, учитывая, что в одном метре $100$ сантиметров:
$$\textcolor{blue}{300} + \textcolor{orange}{50} + \textcolor{green}{4} = \textcolor{blue}{3}\textcolor{orange}{5}\textcolor{green}{4}$$
Мы сложили $3$ сотни, $5$ десятков и $4$ единицы. Такие слагаемые называют разрядными.
пример
Число $673$, содержащее $\textcolor{blue}{6}$ сотен, $\textcolor{coral}{7}$ десятков и $\textcolor{purple}{3}$ единицы можно представить в таком виде:
$$673 = \textcolor{blue}{6 \cdot 100} + \textcolor{coral}{7 \cdot 10} + \textcolor{purple}{3}$$или$$673 = \textcolor{blue}{600} + \textcolor{coral}{70} + \textcolor{purple}{3}$$
пример
Число $5019$ содержит $\textcolor{green}{9}$ единиц, $\textcolor{coral}{1}$ десяток, $\textcolor{blue}{0}$ сотен и $\textcolor{orange}{5}$ тысяч. Получаем:
$$5019 = \textcolor{orange}{5 \cdot 1000} + \textcolor{blue}{0 \cdot 100} + \textcolor{coral}{1 \cdot 10} + \textcolor{green}{9 \cdot 1}$$или$$5019 = \textcolor{orange}{5000} + \textcolor{blue}{0} + \textcolor{coral}{10} + \textcolor{green}{9}$$
Если прибавить к числу нуль, то ничего не изменится, поэтому лучше записать сумму в следующем виде:
$$5019 = \textcolor{orange}{5000} + \textcolor{coral}{10} +\textcolor{green}{9}$$
{"questions":,"placeholder":0,"answer":0}},"step":1,"hints":}]}
Правописание слова пятьдесят
В сложных числительных, состоящих из двух корней, в которых второй частью слова будет «сот» или «десят», следует всегда употреблять мягкий знак в первом корне, но не употреблять его в конце слова.
Слово пятьдесят — это сложное числительное, выражающее счётное количество чего-либо. Морфемный разбор показывает, что оно состоит из двух корней: «пять» и «десят». По сути оно означает пять десятков.
Таким образом, согласно приведённому выше правилу, получаем верное написание слов: пятьдесят, шестьдесят, семьдесят, восемьдесят, пятьсот, шестьсот, семьсот, восемьсот, девятьсот. Как видим, во всех этих словах употребляется мягкий знак в первом корне и не употребляется во втором. Это правило нужно запомнить.
Десятичная запись натурального числа
Любое, даже самое большое число, можно записать с помощью десяти арабских цифр. Никакие дополнительные символы использовать не нужно. Цифры записываются в строчку, слева направо. Последовательность цифр в одном числе может быть абсолютно любой. Бывают и такие числа, в написании которых цифры повторяются.
Ноль, хоть и не является сам по себе натуральным числом, может применяться для обозначения других натуральных чисел.
Рассмотрим примеры:
1 876 542 — один миллион восемьсот семьдесят шесть тысяч пятьсот сорок два. Достаточно большое число, и для его обозначения понадобились только арабские цифры.
373 — триста семьдесят три. Число, для обозначения которого мы дважды использовали цифру 3.
208 — двести восемь. Число, для обозначения которого мы использовали 0.
А вот примеры неправильного применения цифры 0:
07, 011, 0117
Ноль означает пустоту, поэтому его не нужно ставить перед числом.
Примечание: ноль перед числом используется для написания дат: 03.05.2022, 07.10.1981. Это делается, чтобы избежать путаницы.
Практика:
Попросите ребёнка записать с помощью цифр следующие числа: двадцать два, сто восемьдесят семь, пятьсот три, девятнадцать.
Свойства натуральных чисел

Сложение, вычитание, умножение и деление подчиняются законам арифметики. Всего этих законов, основанных на свойствах натуральных чисел, пять.
• Переместительный закон сложения.
При сложении можно менять порядок слагаемых чисел как угодно — результат всегда будет одинаковым.
5 + 7 = 12 и 7 + 5 = 12
24 + 6 + 8 = 38 и 6 + 24 + 8 = 38 и 8 + 6 + 24 = 38
• Переместительный закон умножения.
При умножении можно менять порядок множителей как угодно — результат всегда будет одинаковым.
2 х 4 = 8 и 4 х 2 = 8
4 х 3 х 5 = 60 и 3 х 5 х 4 = 60 и 5 х 4 х 3 = 60
• Сочетательный закон сложения.
При сложении трёх чисел можно сложить первое и второе, и к их сумме прибавить третье, а можно сложить второе и третье, и к их сумме прибавить первое — результат будет один и тот же.
(5 + 7) + 8 = 12 + 8 = 20 и 5 + (7 + ![]() = 5 + 15 = 20
= 5 + 15 = 20
17 + (4 + 23) = 17 + 27 = 44 и (17 + 23) + 4 = 40 + 4 = 44
• Сочетательный закон умножения.
Когда умножаем три числа, то результат не изменится, если перемножать множители не по порядку.
3 х (2 х 5) = 30 и (3 х 5) х 2 = 30
• Распределительный закон.
Результат умножения суммы на число будет равен результату сложения произведений каждого слагаемого суммы на это число.
5 х (3 + 4) = 5 х 3 + 5 х 4 = 35
Вот мы и познакомились с основной информацией о натуральных числах. Мы используем их каждый день: считаем, сколько ложечек сахара положить в чай, сколько бензина залить в машину. С помощью натуральных чисел мы определяем, что выгодней: купить три маленьких коробочки с печеньем или одну большую. Вычисляем, на сколько долек разрезать яблоко, чтобы угостить сестру, маму, папу — и полакомиться самому. Поэтому обязательно учитесь пользоваться натуральными числами — и они обязательно ещё не раз сослужат вам добрую службу.
Знания лучше всего закрепляются в памяти, если ребёнок применяет их на практике, выполняя интересные задания. Такую возможность предоставляет образовательная платформа iSmart. Здесь представлены онлайн-тренажёры, разработанные в соответствии с образовательными стандартами РФ, являющиеся эффективным вспомогательным инструментом для усвоения школьной программы.
Есть разделы по математике, русскому и английскому языкам, окружающему миру, логике и другим предметам. Кроме упражнений для закрепления материала есть также возможность подготовиться к ВПР и контрольным работам.
Зарегистрируйте своего ребёнка на образовательной платформе iSmart, чтобы начать занятия.





























