Примеры проблем, решенных с помощью компенсации
Компенсация — это процесс применения действия силы, противоположной по направлению и равной по величине другой силе, с целью уравновесить или нейтрализовать ее эффект. Этот принцип может применяться для решения различных проблем и ситуаций.
Вот несколько примеров проблем, которые могут быть решены с помощью компенсации:
-
Неработающий электромотор. Если электромотор не работает, это может быть вызвано различными причинами, включая поломку или неправильное подключение. Решение проблемы сводится к компенсации неработающего мотора новым или восстановленным экземпляром, чтобы восстановить функционирование.
-
Потеря равновесия. В некоторых ситуациях объект может потерять равновесие и начать падать или смещаться. Действие силы гравитации может быть скомпенсировано противодействующей силой, чтобы вернуть объект в равновесие.
-
Неправильно сбалансированное рабочее оборудование. Если рабочее оборудование не сбалансировано правильно, оно может вызывать вибрации, неравномерное распределение веса и другие проблемы. Компенсация может включать использование противовесов или других средств для уравновешивания и оптимизации работы оборудования.
-
Ломающиеся трубы. Трубы могут ломаться из-за воздействия силы, например, при разрыве или ударе. С помощью компенсации можно укрепить трубы, устранить повреждения или заменить их более прочными материалами.
-
Неравномерное изношенное оборудование. При эксплуатации механизмы и оборудование могут подвергаться износу и поломкам. Компенсация может включать периодическое техническое обслуживание, замену изношенных деталей или внесение изменений в конструкцию, чтобы повысить прочность и долговечность оборудования.
Это лишь некоторые примеры проблем, в решении которых может быть использована компенсация. В каждой конкретной ситуации необходимо анализировать факторы и выбирать наиболее подходящий метод компенсации для достижения требуемых результатов.
Примеры компенсирующих сил
Примеры компенсирующих сил можно найти в различных областях физики.
Пример компенсирующих сил в равноускоренном движении:
Рассмотрим пример автомобиля, который движется по горизонтальной дороге с постоянным ускорением. В этом случае, движение автомобиля вызывает действие силы трения со стороны дороги, направленной в противоположную сторону движения. Эта сила является компенсирующей силой, так как она противодействует движению автомобиля, создавая равновесие. Без силы трения, автомобиль продолжал бы движение с постоянным ускорением.
Пример компенсирующих сил в статическом равновесии:
Другой пример компенсирующих сил можно найти, рассматривая объект, находящийся в статическом равновесии. Представьте себе шар на столе. В данном случае, сила тяжести действует на шар, направляя его вниз. Однако, сила реакции опоры, которая действует вверх, является компенсирующей силой. Она противодействует силе тяжести и помогает поддерживать шар в статическом равновесии, не позволяя ему упасть.
Это всего лишь два примера компенсирующих сил. В реальном мире существует множество других примеров, где компенсирующие силы играют важную роль в обеспечении равновесия и стабильности систем.
Пример компенсирующих сил в равноускоренном движении
Компенсирующие силы играют важную роль в равноускоренном движении, которое происходит, когда на тело действуют постоянные силы, приводящие к постоянному ускорению.
Рассмотрим пример компенсирующих сил в равноускоренном движении автомобиля. Представим, что автомобиль движется по прямой дороге с постоянным ускорением вперед. В этом случае, на автомобиль действуют две силы: сила тяги, создаваемая двигателем, и сила трения с поверхностью дороги.
Сила тяги направлена вперед и вызывает ускорение автомобиля. Она компенсирует силу трения, которая направлена в обратную сторону. Эти две силы равны по модулю, но имеют противоположные направления, таким образом, они компенсируют друг друга и не позволяют автомобилю либо замедлиться, либо ускориться с постоянным ускорением.
Если сила тяги превышает силу трения, то автомобиль будет ускоряться. В этом случае компенсирующая сила включает силу трения, которая пытается сбалансировать силу тяги. Если сила трения превышает силу тяги, то автомобиль будет замедляться.
Компенсирующие силы в равноускоренном движении помогают поддерживать постоянную скорость и направление движения. Без них невозможно было бы достичь стабильного равноускоренного движения, что делает их важными для множества физических и технических процессов в нашей жизни.
Пример компенсирующих сил в статическом равновесии
Компенсирующие силы играют важную роль в физике, особенно при анализе объектов в статическом равновесии. Статическое равновесие означает, что объект не движется и не вращается. В этом состоянии все силы, действующие на объект, должны быть равны и противоположны по направлению. Компенсирующие силы, таким образом, обеспечивают равновесие.
Чтобы лучше понять, как работают компенсирующие силы в статическом равновесии, рассмотрим пример с прямоугольной табуреткой. Табуретка имеет три ножки, каждая из которых может быть описана как сила, действующая вертикально вниз. В таком случае, каждая нога создает силу, компенсирующую вес табуретки и обеспечивающую ее статическое равновесие.
| Нога | Сила, Н |
|---|---|
| Нога 1 | 100 |
| Нога 2 | 100 |
| Нога 3 | 100 |
В таблице выше представлены силы, создаваемые каждой ножкой табуретки. Общая сила, действующая на табуретку, равна сумме этих сил и равна нулю. Именно поэтому табуретка остается в статическом равновесии и не опрокидывается.
Важно отметить, что значение силы, создаваемой каждой ногой, зависит от веса табуретки и ее распределения по ногам. Если вес табуретки был бы несбалансирован, т.е
табуретка была бы наклонена в одну сторону, компенсирующие силы также будут несбалансированы и табуретка будет выходить из равновесия.
Этот пример демонстрирует, как важно учитывать компенсирующие силы при анализе объектов в статическом равновесии. Они являются неотъемлемой частью физических расчетов и помогают понять, каким образом силы взаимодействуют между собой для создания равновесия
Второй закон Ньютона
В примере с автобусом вы видите, что пассажиры пытаются сохранить свою скорость относительно Земли, инерциальной системы отсчета. Это явление называется инерцией. Инерция — это явление, благодаря которому тело сохраняет состояние покоя или равномерного прямолинейного движения. Инерция — это физическое свойство, согласно которому любое тело сопротивляется изменению своей скорости (как по степени, так и по направлению). Не все тела одинаково инертны. Вы можете взять мяч и придать ему большое ускорение. Но вы не можете придать гире такое же ускорение, даже если она схожа по размеру. Однако мяч и гиря различаются по массе. Масса — это масштабируемая физическая величина, которая является мерой инерции тела. Чем больше масса, тем больше инерция тела. Масса обозначается буквой m. Единицей измерения массы является кг. Одним из инструментов для измерения массы являются весы. Чтобы придать двум телам с разной инерцией одинаковую скорость, необходимо приложить большую силу к телу с большей инерцией. Попробуйте передвинуть стол, а затем шкаф. Стол будет легче перемещать. Если приложить одинаковую силу к телу с разной инерцией, то можно обнаружить, что тело с меньшей инерцией испытает большее ускорение. Если положить теннисный мяч на пружину, сжать ее и резко отпустить, мяч улетит. Если вы возьмете железный мяч вместо теннисного, он прокатится только на определенное расстояние. Описанные выше примеры показывают, что существует взаимосвязь между силой, приложенной к телу, и ускорением, которое оно испытывает в результате приложения силы, и массой тела. Это видно из второго закона движения Ньютона. Второй закон Ньютона Сила, действующая на тело, равна произведению массы тела на ускорение, вызванное силой. F = ma, где F — сила, действующая на тело, a — ускорение, вызванное этой силой, m — масса тела Сила — это количественная мера действия тел друг на друга, в результате которого тела испытывают ускорения. Сила — это векторная физическая величина. Он обозначается как F. Единицей измерения является Н (Ньютон). Инструментом для измерения силы является динамометр. Пример 1. Определите силу, с которой Земля действует на яблоко, когда оно падает с ветки, а ускорение яблока равно 9,8 м/с2. Масса яблока равна 200 г. Переведите массу яблока в кг. 200 г = 0,2 кг. Теперь найдем силу, с которой Земля действует на яблоко в соответствии со вторым законом движения Ньютона.
Иногда на одно тело действует много сил. В этом случае в описание движения вводится понятие конституирующей силы. Определение Эквивалентная сила — это векторная сумма всех сил, одновременно действующих на тело. R = F1+ F2+ F3+ … В этом случае второй закон Ньютона формулируется следующим образом: Второй закон движения Ньютона обусловлен составляющими силами Если на тело действует множество сил, то их составляющая R равна произведению массы на ускорение тела. m a = R = F1+ F2+ F3+ …
Правила сложения сил и их проекций
| Сложение двух сил, направленных вдоль прямой линии в одном направлении | |
| Если F1↑↑ F2тогда: R = F1+ F2Результирующая сила является обратной величиной двух сил. | |
| Сложение двух сил, действующих вдоль прямой линии в противоположных направлениях. | |
| Если F1↑↓ F2тогда: R = | F1– F2| Результирующая сила направлена в сторону большей силы. | |
| Сложение двух сил, которые перпендикулярны друг другу | |
| Если F1перпендикулярна F2то результирующая сила вычисляется по теореме Пифагора: | |
| Сложение двух сил, расположенных под углом a друг к другу | |
| Если F1и F2образуют между собой угол a, результирующая сила рассчитывается по теореме косинусов: | |
| Сложение трех сил | |
| Способ сложения определяется правилами сложения векторов. В данном случае: | |
| Добавление проекций силы | |
 |
Проекция на ось OX: F1x+ F2x– F3x= 0 Проекция на ось OY: F1y– F2y= 0 |
Практическое применение компенсации действия сил
Компенсация действия сил – это принцип, который применяется в разных областях человеческой деятельности. Идея заключается в том, чтобы найти способы балансировки и снижения негативного воздействия сил, вызываемых внешними факторами. Это может быть полезно при решении различных проблем и достижении желаемого результата.
Одним из практических примеров применения компенсации действия сил является архитектура зданий. При проектировании здания необходимо учесть возможные внешние воздействия, такие как ветер, землетрясения и другие неблагоприятные факторы. Инженеры и архитекторы используют различные техники, чтобы сделать здание устойчивым к таким силам. Например, они могут использовать усиленные фундаменты, стабилизаторы наружных стен и другие приспособления, чтобы смягчить негативное воздействие на здание.
Еще одним примером применения компенсации действия сил является автомобильный дизайн. Автомобильные производители стремятся сделать свои автомобили безопасными для пассажиров в случае аварии. Они используют различные технологии, чтобы компенсировать силу удара и уменьшить повреждения. Например, в автомобилях устанавливают системы подушек безопасности, усиленные кузовы и другие меры, чтобы минимизировать последствия аварийных ситуаций.
В различных спортивных дисциплинах также используется компенсация действия сил. Например, в гимнастике спортсмены могут использовать различные приспособления, такие как подковы, ленты или подушки, чтобы смягчить воздействие силы на свое тело. В теннисе игроки могут изменять угол отскока мяча, чтобы сделать его более предсказуемым и контролируемым.
Применение компенсации действия сил имеет широкие практические применения и позволяет достигать лучших результатов в различных сферах жизни. Этот принцип помогает преодолеть негативные воздействия сил и создать более устойчивые и безопасные условия для решения проблем и достижения поставленных целей.
Сила атмосферного давления и ее эффекты на движение
Одним из ключевых эффектов силы атмосферного давления является трение воздуха. Когда тело движется через атмосферу, воздух сопротивляет его движению, создавая силу трения. Это может вызывать замедление движения или его полное прекращение.
Сила атмосферного давления также может влиять на днамическое и статическое равновесие тела. Например, когда на тело действует сила атмосферного давления с одной стороны, а другая сторона не подвержена этому давлению, возникает разница во воздушном давлении на обеих сторонах тела. Это может привести к движению тела или его вращению.
Еще одним важным эффектом атмосферного давления на движение является возникновение аэродинамической силы. Когда тело движется через атмосферу, воздух, проходя через тело, создает подъемную силу, которая может поддерживать тело в воздухе или помогать ему двигаться вперед. Этот эффект используется, например, в авиации или в водных виде спортах, таких как парусный спорт.
В целом, сила атмосферного давления является важным фактором, влияющим на движение тела в нашей окружающей среде. Она может создавать сопротивление, влиять на равновесие тела и даже помогать движению через атмосферу. Понимание этих эффектов силы атмосферного давления помогает в разработке различных технических устройств и решении физических задач в различных областях науки и техники.
Взаимодействие сил и его влияние на движение
Взаимодействие сил играет важную роль в определении движения тела. Когда на тело действуют различные силы, они могут либо сбалансироваться и оставить тело в состоянии покоя, либо вызвать ускорение и изменение его скорости и направления.
Сила — это векторная величина, которая описывает воздействие одного тела на другое и может быть как силой тяжести, так и силой трения, силой электромагнитного поля и др. Для полного описания векторной силы необходимо указать ее направление, точку приложения и величину.
Когда на тело действует только одна сила, оно будет двигаться в направлении и с ускорением, определяемыми этой силой. Однако, в реальных условиях на тело часто действуют несколько сил одновременно. В таком случае, совокупность всех векторных сил приводит к образованию результирующей силы.
Если результирующая сила, действующая на тело, равна нулю, то его движение будет равномерным и прямолинейным. Если она отлична от нуля, то тело будет двигаться с ускорением в направлении этой силы. Значение ускорения будет определяться массой тела и величиной результирующей силы в соответствии со вторым законом Ньютона.
Кроме того, взаимодействие сил может приводить к изменению направления движения тела. Например, при движении в градиенте силы тяжести возникает ускорение в направлении вектора градиента, что приводит к изменению траектории движения.
Взаимодействие сил и его влияние на движение тела представляют собой одну из основных тем механики. Понимание этих принципов позволяет объяснить множество физических явлений и применить их в практических ситуациях.
Как действует сила на движение тела?
Сила играет важную роль в движении тела. Она может изменить скорость, направление или форму движения объекта.
Сила может быть применена к телу различными способами, такими как толчок, тяга или вращение. Она может быть направлена вдоль оси движения или в противоположном направлении. Сила может также вызывать внутреннее напряжение в теле, например, при сжатии или растяжении.
В динамике, сила обозначается вектором и имеет как величину, так и направление. Например, сила может быть направлена вперед или назад, вверх или вниз, вправо или влево. Векторная сила также может иметь различную величину, которая может быть измерена в ньютонах.
Когда сила действует на тело, она может вызывать изменение его скорости. Если сила направлена в том же направлении, что и скорость тела, она может увеличить его скорость. Если сила направлена в противоположном направлении, она может замедлить или остановить тело.
Сила также может изменять направление движения тела. Например, если сила действует под углом к направлению движения, она может вызвать изменение направления движения тела, не изменяя его скорости.
| Виды сил | Описание |
|---|---|
| Гравитационная сила | Притяжение тел друг к другу из-за их массы |
| Электромагнитная сила | Действие между заряженными частицами |
| Сила трения | Сила, возникающая при движении тела по поверхности |
| Сила упругости | Сопротивление тела изменению его формы |
| Центробежная сила | Сила, направленная от центра вращения тела |
| Центростремительная сила | Сила, направленная к центру вращения тела |
Взаимодействие между силой и движением тела описывается законами Ньютона. Согласно первому закону Ньютона, если на тело не действует никаких внешних сил, оно будет двигаться прямолинейно со постоянной скоростью или оставаться в покое. Согласно второму закону Ньютона, при действии силы на тело происходит изменение его импульса, пропорциональное величине силы и обратно пропорциональное его массе. Согласно третьему закону Ньютона, каждая сила имеет равную и противоположную ей силу, называемую противодействующей силой.
Первый закон Ньютона
Когда Исаак Ньютон изучал движение тел, он обнаружил, что свободные тела сохраняют свою скорость относительно одних систем отсчета, но не относительно других. Он разделил их на две большие группы: Инерционные системы и неинерционные системы. Именно здесь кроется первый закон движения Ньютона. Первый закон движения Ньютона Существуют системы отсчета, называемые инерциальными системами, вокруг которых тела движутся равномерно и прямолинейно или находятся в состоянии покоя, когда другие тела не действуют на них или их действие компенсируется. Примером инерциальной системы отсчета является система отсчета, связанная с Землей (геоцентрическая). Другой пример — гелиоцентрическая система отсчета (связанная с Солнцем). Неинерциальная система отсчета — это система отсчета, в которой тела могут изменять свою скорость без воздействия других тел.
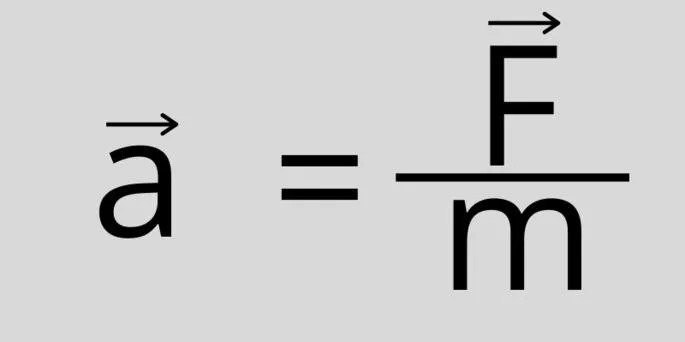
Импульс силы. Импульс тела
Понятие импульса было введено еще в первой половине XVII века Рене Декартом, а затем уточнено Исааком Ньютоном. Согласно Ньютону, который называл импульс количеством движения, – это есть мера такового, пропорциональная скорости тела и его массе. Современное определение: импульс тела – это физическая величина, равная произведению массы тела на его скорость:
= m
Прежде всего, из приведенной формулы видно, что импульс – величина векторная и его направление совпадает с направлением скорости тела, единицей измерения импульса служит:
= [ кг· м/с]
Рассмотрим, каким же образом эта физическая величина связана с законами движения. Запишем второй закон Ньютона, учитывая, что ускорение есть изменение скорости с течением времени:
Налицо связь между действующей на тело силой, точнее, равнодействующей сил и изменением его импульса. Величина произведения силы на промежуток времени носит название импульса силы. Из приведенной формулы видно, что изменение импульса тела равно импульсу силы.
Какие эффекты можно описать с помощью данного уравнения (рис. 1)?
Рис. 1. Связь импульса силы с импульсом тела (Источник)
Стрела, выпускаемая из лука. Чем дольше продолжается контакт тетивы со стрелой (∆t), тем больше изменение импульса стрелы (∆ ), а следовательно, тем выше ее конечная скорость.
Два сталкивающихся шарика. Пока шарики находятся в контакте, они действуют друг на друга с равными по модулю силами, как учит нас третий закон Ньютона. Значит, изменения их импульсов также должны быть равны по модулю, даже если массы шариков не равны.
Проанализировав формулы, можно сделать два важных вывода:
- Одинаковые силы, действующие в течение одинакового промежутка времени, вызывают одинаковые изменения импульса у различных тел, независимо от массы последних.
- Одного и того же изменения импульса тела можно добиться, либо действуя небольшой силой в течение длительного промежутка времени, либо действуя кратковременно большой силой на то же самое тело.
Согласно второму закону Ньютона, можем записать:
∆t = ∆ = ∆ / ∆t
Отношение изменения импульса тела к промежутку времени, в течение которого это изменение произошло, равно сумме сил, действующих на тело.
Проанализировав это уравнение, мы видим, что второй закон Ньютона позволяет расширить класс решаемых задач и включить задачи, в которых масса тел изменяется с течением времени.
Если же попытаться решить задачи с переменной массой тел при помощи обычной формулировки второго закона Ньютона:
= m,
то попытка такого решения привела бы к ошибке.
Примером тому могут служить уже упоминаемые реактивный самолет или космическая ракета, которые при движении сжигают топливо, и продукты этого сжигаемого выбрасывают в окружающее пространство. Естественно, масса самолета или ракеты уменьшается по мере расхода топлива.
Вывод второго закона Ньютона
С помощью закона сохранения импульса и взаимосвязи импульса силы и импульса тела мы можем вывести второй и третий закон Ньютона.
Второй закон Ньютона выводится из соотношения импульса силы и импульса тела.
Импульс силы равен изменению импульса тела:
Произведя соответствующие переносы, мы получим зависимость силы от ускорения, ведь ускорение определяется как отношение изменения скорости ко времени, в течение которого это изменение произошло:
Подставив значения в нашу формулу, получим формулу второго закона Ньютона:
Вывод третьего закона Ньютона
Для выведения третьего закона Ньютона нам понадобится закон сохранения импульса.
Векторы подчеркивают векторность скорости, то есть то, что скорость может изменяться по направлению. После преобразований получим:
Так как промежуток времени в замкнутой системе был величиной постоянной для обоих тел, мы можем записать:
Мы получили третий закон Ньютона: два тела взаимодействуют друг с другом с силами, равными по величине и противоположными по направлению. Векторы этих сил направлены навстречу друг к другу, соответственно, модули этих сил равны по своему значению.
Третий закон Ньютона
По второму закону Ньютона можно рассчитать ускорение движущегося тела и при известных начальных условиях найти его скорость и координаты в любой момент времени.
Но на практике недостаточно знать закон движения, например, автомобиля
Важно знать также силу, с которой он действует на опору, чтобы рассчитать, например, конструкцию моста, по которому автомобиль движется. Следовательно, необходимо установить, как соотносятся между собой силы, с которыми действуют друг на друга тела при взаимодействии.
Проведем некоторые опыты и исследуем этот вопрос
Закрепим в двух штативах динамометры, соединенные крючками (рис. 47, а). Если потянуть в горизонтальном направлении поочередно за один динамометр, за другой или за оба вместе, то в каждом опыте показания приборов равны. Значит, силы, с которыми динамометры действуют друг на друга, равны по модулю и по условиям опыта направлены в противоположные стороны.
Присоединим к одному динамометру кусок железа, а к другому — магнит. При взаимодействии железа и магнита на динамометрах также установятся одинаковые показания (рис. 47, б).
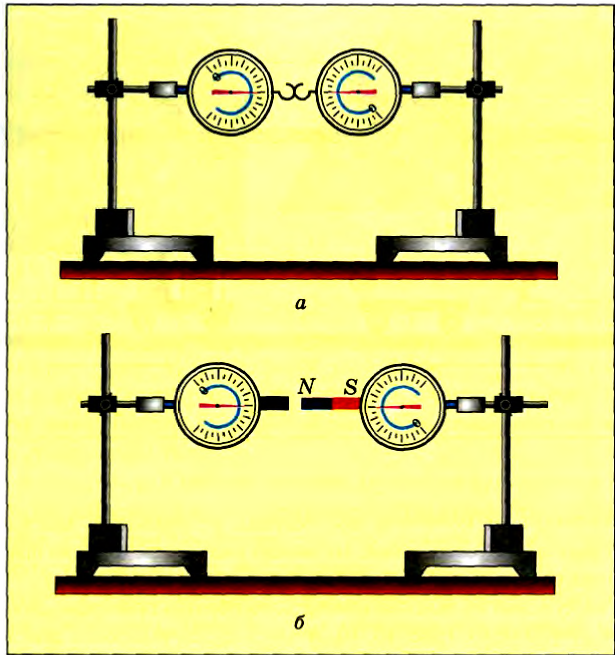
Рис. 47
Рассмотрим другой опыт. Пусть на гладких горизонтальных рельсах, закрепленных на неподвижном столе, расположены две тележки одинаковой массы. Закрепим на одной из них моторчик, на ось которого при его работе будет наматываться нить, привязанная к другой тележке. На тележку без моторчика поставим дополнительную гирю, масса которой равна массе моторчика, чтобы общие массы тележек были равны.
При работающем моторчике обе тележки устремляются навстречу друг другу с одинаковыми ускорениями. Их можно рассчитать, измерив пройденный путь и время его прохождения (рис. 48, а).
Если массу одной из тележек изменить, то обратно пропорционально массе изменится ее ускорение (рис. 48, б). А для модулей ускорений двух тележек, если их массы различны, выполняется следующее соотношение:
или m1a1=m2a2
Если учесть, что по второму закону Ньютона m1a1=F1 и m2a2 = F2, а ускорения тележек направлены в противоположные стороны, то можно записать:
Какие бы примеры взаимодействия тел не рассматривались, всегда выполняется установленный Ньютоном третий закон:силы, с которыми два тела действуют друг на друга, одной природы, равны по модулю, противоположны по направлению и направлены вдоль одной прямой.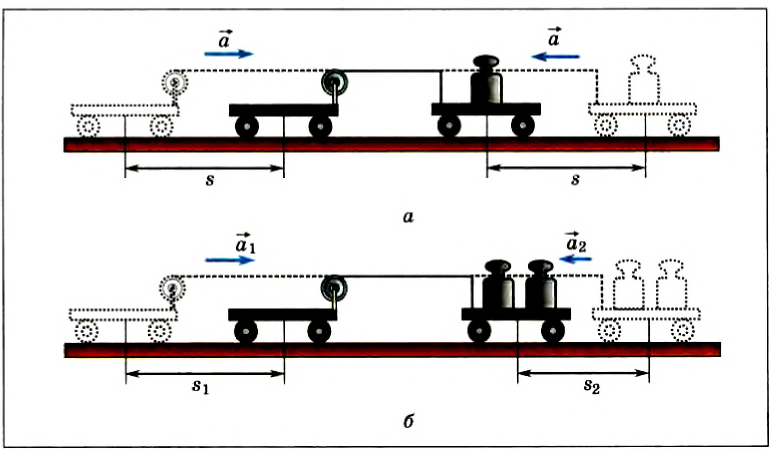
Рис. 48
Из третьего закона Ньютона следует, что силы всегда возникают парами и при взаимодействии тел равноправны.
Значит, например, с какой силой каждого человека притягивает наша огромная планета Земля, с такой же силой и человек притягивает Землю.
Третий закон Ньютона выполняется для любых взаимодействий, в том числе и для столкновений тел.
Почему, например, в районах больших аэропортов принимаются специальные меры для удаления из воздушного пространства любых птиц? Столкновение даже небольшой птицы с обшивкой самолета, стеклом иллюминатора или частью двигателя может вызвать их разрушение.
Ускорение и деформация тел при взаимодействии зависят от их массы и от того, с какими другими телами есть еще взаимодействие в данный момент.
Рассмотрим, например, взаимодействие одинаковых бильярдных шаров при различных условиях (рис. 49). Шар, лежащий посередине стола, взаимодействует с опорой и притягивается Землей. Причем силы тяжести и упругости перпендикулярны плоскости стола и равны по модулю. Можно показать, что при центральном ударе по одному шару такого же второго шара бильярдные шары практически обмениваются скоростями (рис. 50).
|
Рис. 49 |
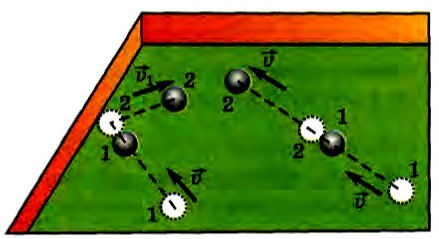 Рис. 50 |
Если шар лежит у бортика стола, взаимодействуя добавочно и с ним (см. рис. 50), то результат удара совершенно другой. Хотя при этом массы тел не изменились, и скорость движущегося шара перед взаимодействием такая же.
Экспериментально установлено: в каких бы разнообразных взаимодействиях тело не участвовало, третий закон Ньютона выполняется для каждой пары взаимодействующих тел.
Таким образом, третий закон Ньютона утверждает, что силы возникают всегда парами. Любое взаимодействие необходимо характеризовать двумя силами, которые хотя и равны по модулю, но противоположны по направлению и действуют на разные тела.
Главные выводы
- Силы взаимодействия двух тел равны по величине, противоположно направлены и приложены к разным телам.
- Третий закон Ньютона выполняется в инерциальных системах отсчета.
- Результат взаимодействия двух тел зависит от того, в каких еще взаимодействиях каждое из них участвует.
Фундаментальные взаимодействия
- Все силы в природе основаны на четырех типах фундаментальных взаимодействий. Максимальная скорость распространения всех видов взаимодействия равнаскорости света в вакууме. Электромагнитные силы действуют междуэлектрически заряженнымителами, гравитационные − междумассивнымиобъектами.Сильноеислабое проявляются только на очень малыхрасстояниях, они ответственны за возникновение взаимодействия междусубатомными частицами, включаянуклоны, из которых состоят атомные ядра.
Интенсивность сильного и слабого взаимодействия измеряется вединицах энергии(электрон-вольтах), а неединицах силы, и потому применение к ним термина «сила» объясняется берущей из античности традицией объяснять любые явления в окружаемом мире действием специфических для каждого явления «сил».
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.





























