Значок «примерно» («приблизительно»): как пишется, примеры

Значок «примерно»
Значок «примерно» пишется так: «≈». Похож на знак равно, но вместо прямых линий используются волнистые. Этот знак используется тогда, когда разницу между двумя числами можно не учитывать, потому что она слишком мала или незначительна.
Например:
На все человечество действует сила тяжести, именно из-за нее люди не улетают в открытый космос с Земли. При этом эта сила тяжести зависит от ускорения свободного падения, равного 9,8 метров в секунду в квадрате. Но в школе для упрощения расчетов и из-за незначительной разницы в результате вычислений ускорение свободного падения принимается за 10 метров в секунду в квадрате. То есть, можно сказать, что 9,8 метров в секунду ≈ 10 метрам в секунду.

П равно
Знак «примерно равно» используется, когда число округляется до определенного количества знаков. Например, со школьной скамьи всем известно число Пи — константа с бесконечным числом знаков после запятой. Обычно это число округляется до двух знаков после запятой. То есть можно записать, что Пи ≈ 3,14.
Когда нужно менять знаки неравенства?
Может ли неравенство иметь знак равенства?
Символы неравенства — это символы, которые используются для обозначения отношений неравенства. … Хотя знак равенства технически не является неравенством символ, он обсуждается вместе с символами неравенства, поскольку он включен как часть нестрогих неравенств, таких как больше или равно (≥) и меньше или равно (≤).
Это между или между?
Между ними всегда должно быть два слова.. Хотя inbetween встречается часто, это опечатка, и ее нет ни в одном словаре английского языка. Ненужное добавление между ними также является распространенной грамматической ошибкой.
Что означает разница в математике?
Разница в том, результат вычитания одного числа из другого. … Итак, разница — это то, что остается от одного числа при вычитании из другого. В уравнении вычитания есть три части: уменьшаемое (число, из которого вычитается) вычитаемое (число, из которого вычитается)
В чем разница между этими двумя символами и ==?
Ответ: = символ часто используется в математических операциях. Он используется для присвоения значения заданной переменной. С другой стороны, символ ==, также известный как «равно» или «эквивалентно», представляет собой оператор отношения, который используется для сравнения двух значений.
Для чего нужен хаммерский сленг?
переходный глагол. Если вы говорите, что кто-то бьет другого человека, вы имеете в виду, что они атаковать, критиковатьили строго наказать другого человека. Демократы настаивали на том, что они будут продолжать бить президента по его налоговому плану.
Что означает этот символ ≅?
Символ ≅ официально определяется как U+2245 ≅ ПРИБЛИЗИТЕЛЬНО РАВНО. Это может означать: Приблизительное равенство. Конгруэнтность (геометрия)
Что такое V в математике?
Символы «V» в вопросе читателя — это ∨ и ∧, что означает «Логическое ИЛИ» и «Логическое И.» ∧ — заглавная греческая лямбда.
Не больше, чем то же самое, что и меньше?
Когда мы говорим «столько же, сколько» или «не более чем», мы имеем в виду «меньше или равно‘, что означает, что a может быть меньше b или равно b. Но когда мы говорим «по крайней мере», мы имеем в виду «больше или равно».
Добавляет больше, чем означает?
Сложение-сумма, всего, всего, всего, вместе, всего, общего числа, прибавления, прибавления, вырос по, более чем. Вычитание-минус, больше, отнять, меньше, меньше, вычесть, уменьшить на.
Какой знак наименьший?
Какой знак представляет хотя бы? Обозначение а ≥ b или а ⩾ b означает, что a больше или равно b (или, что то же самое, по крайней мере b или не меньше b).
Произведение означает умножение?
Продукт в математике число, которое получается путем умножения двух или более других чисел вместе. Например, если вы умножите 2 и 5 вместе, вы получите произведение 10. Умножение — важная часть математики.
Что значит найти разницу?
Нахождение разницы между двумя числами форма вычитания. В этих задачах по математике цель состоит в том, чтобы найти, сколько чисел лежит между двумя заданными числами. Это похоже на поиск диапазона между двумя числами.
В чем разница между 5 и 3?
если нам говорят найти разницу между 3 и 5, то мы обычно вычитаем 3 из 5,5-3=2 и, таким образом, мы говорим, что разница равна 2.
Можете ли вы закончить предложение с промежуточным звеном?
Окончание предложения предлогом не является ошибкой, но это немного менее формально. В электронных письмах, текстовых сообщениях и заметках для друзей все в порядке. Но если вы пишете исследовательскую работу или подаете деловое предложение и хотите, чтобы это звучало очень официально, избегайте заканчивать предложения предлогами.
Какое другое слово для между ними?
Промежуточные синонимы
На этой странице вы можете найти 6 синонимов, антонимов, идиоматических выражений и родственных слов для промежуточных значений, например: посредничать, середина, посередине, через, между и пространство между ними.
Как узнать, верно ли неравенство?
Если обе части неравенства умножаются или делятся на одно и то же положительное число, то полученное неравенство верно. Если обе части умножить или разделить на одно и то же отрицательное значение, направление неравенства изменится.
Что означает знак не равно?
Неравный, не равный. Некоторые сторонники превосходства белой расы приняли математический знак «≠(Not Equal or Not Equal To) как символ сторонников превосходства белой расы. Использование этого символа является попыткой заявить, что разные расы не равны друг другу (и подразумевать превосходство белой расы).
Символы вероятности и статистики
| Символ | Название символа | Значение / определение | пример |
|---|---|---|---|
| P ( А ) | функция вероятности | вероятность события A | P ( A ) = 0,5 |
| P ( A ⋂ B ) | вероятность пересечения событий | вероятность того, что событий A и B | P ( A ⋂ B ) = 0,5 |
| P ( A ⋃ B ) | вероятность объединения событий | вероятность того, что событий A или B | P ( A ⋃ B ) = 0,5 |
| P ( A | B ) | функция условной вероятности | вероятность события A данное событие B произошло | P ( A | B ) = 0,3 |
| f ( x ) | функция плотности вероятности (pdf) | P ( a ≤ x ≤ b ) = ∫ f ( x ) dx | |
| F ( х ) | кумулятивная функция распределения (cdf) | F ( х ) = Р ( Х ≤ х ) | |
| μ | Средняя численность населения | среднее значение совокупности | μ = 10 |
| E ( X ) | ожидаемое значение | ожидаемое значение случайной величины X | E ( X ) = 10 |
| E ( X | Y ) | условное ожидание | ожидаемое значение случайной величины X с учетом Y | E ( X | Y = 2 ) = 5 |
| var ( X ) | отклонение | дисперсия случайной величины X | var ( X ) = 4 |
| σ 2 | отклонение | дисперсия значений совокупности | σ 2 = 4 |
| std ( X ) | стандартное отклонение | стандартное отклонение случайной величины X | std ( X ) = 2 |
| σ X | стандартное отклонение | значение стандартного отклонения случайной величины X | σ X = 2 |
| медиана | среднее значение случайной величины x | ||
| cov ( X , Y ) | ковариация | ковариация случайных величин X и Y | cov ( X, Y ) = 4 |
| корр ( X , Y ) | корреляция | корреляция случайных величин X и Y | корр ( X, Y ) = 0,6 |
| ρ X , Y | корреляция | корреляция случайных величин X и Y | ρ X , Y = 0,6 |
| ∑ | суммирование | суммирование — сумма всех значений в диапазоне ряда | |
| ∑∑ | двойное суммирование | двойное суммирование | |
| Пн | Режим | значение, которое чаще всего встречается в популяции | |
| MR | средний диапазон | MR = ( x макс + x мин ) / 2 | |
| Мкр | медиана выборки | половина населения ниже этого значения | |
| Q 1 | нижний / первый квартиль | 25% населения ниже этого значения | |
| 2 квартал | медиана / второй квартиль | 50% населения ниже этого значения = медиана выборки | |
| 3 квартал | верхний / третий квартиль | 75% населения ниже этого значения | |
| х | выборочное среднее | среднее / среднее арифметическое | х = (2 + 5 + 9) / 3 = 5,333 |
| с 2 | выборочная дисперсия | оценщик дисперсии выборки населения | s 2 = 4 |
| с | стандартное отклонение выборки | Оценка стандартного отклонения выборки населения | s = 2 |
| z x | стандартная оценка | z x = ( x — x ) / s x | |
| X ~ | распределение X | распределение случайной величины X | X ~ N (0,3) |
| N ( μ , σ 2 ) | нормальное распределение | гауссово распределение | X ~ N (0,3) |
| U ( а , б ) | равномерное распределение | равная вероятность в диапазоне a, b | Х ~ U (0,3) |
| ехр (λ) | экспоненциальное распределение | f ( x ) = λe — λx , x ≥0 | |
| гамма ( c , λ) | гамма-распределение | f ( x ) = λ cx c-1 e — λx / Γ ( c ), x ≥0 | |
| χ 2 ( к ) | распределение хи-квадрат | f ( x ) = x k / 2-1 e — x / 2 / (2 k / 2 Γ ( k / 2)) | |
| F ( k 1 , k 2 ) | F распределение | ||
| Корзина ( n , p ) | биномиальное распределение | f ( k ) = n C k p k (1 -p ) nk | |
| Пуассон (λ) | распределение Пуассона | е ( К ) знак равно λ К е — λ / К ! | |
| Геом ( p ) | геометрическое распределение | f ( k ) = p (1 -p ) k | |
| HG ( N , K , n ) | гипергеометрическое распределение | ||
| Берн ( p ) | Распределение Бернулли |
Сравнение положительных чисел с нолем
Чтобы не испытывать трудностей при выполнении сравнения положительных чисел и нуля, давайте рассмотрим задачу.
У Марины в кармане было четыре конфеты, а в Наташином кармашке лежало 0 конфет. Подумайте и объясните, у кого из девочек имелось большее количество конфет.
Изучив условие задачи, мы понимаем, что для ответа на главный вопрос задачи нужно выполнить сравнение количества Марининых сладостей с количеством сладостей, имеющихся у Натальи, то есть 4 и 0.
Давайте определим, к каким числам можно отнести значение четыре? К положительным или отрицательным?
Вспомним определение положительного:
Положительными числами называют числа со знаком +.На письме, не принято ставить знак «плюс» перед положительными числами. Считается, что если перед числом не стоит знак «минус», то число является положительным.
Исходя из определения, рассматриваемое значение считается положительным.
Переходим ко второму числу: 0.
Обязательно нужно понимать, что такое 0.
0 является целым числом, но при этом, не обозначает количество предметов.
Если будем рассматривать ноль в обычной жизни, то можно сказать иначе: 0 = «ничего».
в кассе 0 рублей = касса пуста, денег нет;
улов дедушки составил 0 рыб = дедушка ничего не поймал;
мальчик вынес во двор 0 игрушек = мальчик не вынес во двор игрушки.
Делаем вывод, что у Наташи не было конфет, а у Марины было 4 леденца.
Теперь можно выполнить сравнение положительного числа 4 с числом 0.
Даже ребенок понимает, что четыре конфетки больше, чем ничего или 0.
Из рассмотренного пояснения следует:
любое положительное число всегда будет больше, чем ноль!
Пример 2: Голодный крокодил
Может ли число быть больше и меньше одновременно, если используется выражение «не менее»?
Нет, число не может быть больше и меньше одновременно, если используется выражение «не менее». Выражение «не менее» указывает на минимальное значение, которое может быть равным данному. То есть число может быть равно данному значению или больше его, но не меньше.
Голодный крокодил каждый день ест не менее 5 рыбок. Если он уже съел 10 рыбок, сколько рыбок ему необходимо съесть еще минимум?
Для решения этой задачи, нужно вычесть количество уже съеденных рыбок из минимального количества рыбок, которые он должен съесть: 5 — 10 = -5.
Значение -5 означает, что голодный крокодил уже съел 5 рыбок больше, чем он должен был. В данном случае, крокодилу не нужно есть ничего дополнительно.
Правило и свойство сложения числовых неравенств
Рассмотрим некое числовое неравенство в виде:
a < b
Попробуем сложить записанное неравенство с каким-то числом с. Для этого прибавим это число к левой и правой частям неравенства. Получим:
a + c < b + c
Запишем следующее неравенство:
c < d
Суммируем обе его части с неким числом b. В результате получим:
b + c < b + d
Проанализируем полученные неравенства со слагаемым:
a + c < b + c
b + c < b + d
Заметим, что из этого следует:
a + c < b + d
Таким образом, можно сформулировать объяснение свойства сложения неравенств: результатом почленного сложения верных неравенств, которые имеют знаки в одну сторону, является верное неравенство.
Математические знаки
Скорее всего, к первому классу ребенок уже отличает на слух и визуально, что горстка из десяти ягод больше трех штук. Чтобы внедрить в жизнь новые обозначения, посмотрим на знаки «больше», «меньше», «равно» в картинках.
Символ больше (>) — это когда острый нос галочки смотрит направо. Его нужно использовать, когда первое число больше второго:
Символ меньше (<) — это когда острый нос галочки смотрит налево. Его нужно использовать, когда первое число меньше второго:
Символ равенства (=) — это когда два коротких отрезка записаны горизонтально и параллельны друг другу. Используем его при сравнении двух одинаковых чисел:
Чтобы ребенку было легче запомнить схожие между собой знаки, можно применить игровой метод. Для этого нужно сравнить числа и определить в каком порядке они стоят. Далее ставим одну точку у наименьшего числа и две — рядом с наибольшим. Соединяем точки и получаем нужный знак. Вот так просто: 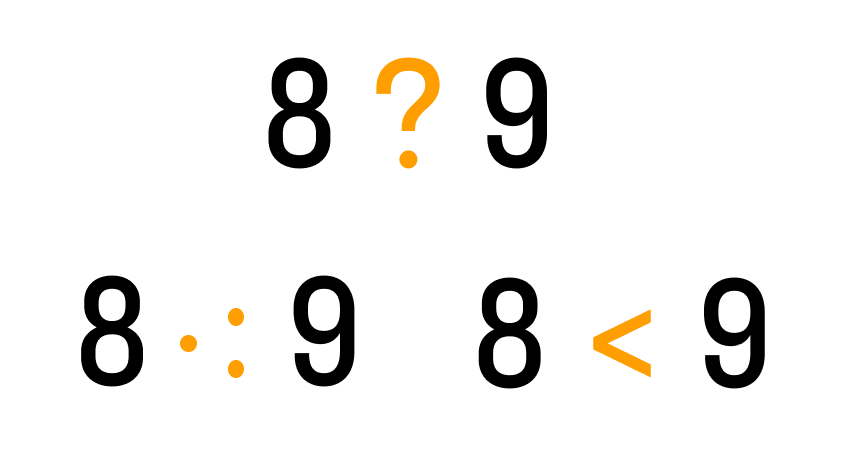
Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.

Определение нулевых чисел и их важность
Нулевые числа — это числа, которые имеют значение 0. Они являются особыми числами в математике и играют важную роль в различных областях науки и практической деятельности.
Нулевые числа считаются обычно исключительными, потому что они не имеют значения в обычном смысле. Однако, без нулевых чисел многие математические и физические концепции были бы неполными или даже невозможными.
Вот несколько примеров, демонстрирующих важность нулевых чисел:
Символическое обозначение: Ноль является символическим обозначением для отсутствия или пустоты
Он используется для обозначения нулевой суммы, нулевого количества или нулевой степени в различных математических операциях и формулах.
Место-значимость: Ноль имеет важное значение в позиционной системе счисления, такой как десятичная система. Он помогает определять место-значение других цифр и расширяет диапазон представления чисел.
Графики и функции: Нулевые числа играют важную роль в построении графиков и решении уравнений
Они помогают определить точки пересечения графиков, корни уравнений и решения систем уравнений.
Физические законы: Многие физические законы и формулы включают нулевые значения. Например, закон сохранения энергии или закон Второго начала термодинамики связаны с отсутствием энергии или изменениями энтропии.
Все эти примеры показывают, что нулевые числа не являются просто ничтожными или бесполезными. Они играют роль основных элементов в математике, науке и повседневной жизни, и их понимание является важным для достижения точности, логического мышления и аналитических навыков.
Решение более сложных примеров
Попробуем упростить выражение \( \left| \sqrt{3}-2 \right|+\left| \sqrt{3}+5 \right|\)
Решение:
Итак, мы помним, что значение модуля не может быть меньше нуля. Если под знаком модуля число положительное, то мы просто можем отбросить знак: модуль числа будет равен этому числу.
Но если под знаком модуля отрицательное число, то значение модуля равно противоположному числу (то есть числу, взятому со знаком «–»).
Для того, чтобы найти модуль любого выражения, для начала нужно выяснить, положительное ли значение оно принимает, или отрицательное.
\( \displaystyle \sqrt{3} \approx 1,7\). Получается, значение первого выражения под модулем \( \displaystyle \sqrt{3}-2\approx 1,7-2\approx -0,3\text{ }\).
\( -0,3<0\), следовательно, выражение под знаком модуля отрицательно. Второе выражение под знаком модуля всегда положительно, так как мы складываем два положительных числа.
Итак, значение первого выражения под знаком модуля отрицательно, второго – положительно:
Математические знаки
Скорее всего, к первому классу ребенок уже отличает на слух и визуально, что горстка из десяти ягод больше трех штук. Чтобы внедрить в жизнь новые обозначения, посмотрим на знаки «больше», «меньше», «равно» в картинках.
Символ больше (>) — это когда острый нос галочки смотрит направо. Его нужно использовать, когда первое число больше второго:
Символ меньше (
Символ равенства (=) — это когда два коротких отрезка записаны горизонтально и параллельны друг другу. Используем его при сравнении двух одинаковых чисел:
Чтобы ребенку было легче запомнить схожие между собой знаки, можно применить игровой метод. Для этого нужно сравнить числа и определить в каком порядке они стоят. Далее ставим одну точку у наименьшего числа и две — рядом с наибольшим. Соединяем точки и получаем нужный знак. Вот так просто:
Целые положительные и отрицательные значения
Рассмотрим подробно какие числа мы можем назвать отрицательны, а какие положительным. Сформулируем основные определения и приведем наглядные примеры.
Определение
Простое положительное число — это как правило число, которое располагается с правой стороны от нулевого значения. Ему присвоен знак плюс, иными словами числа с плюсовым значением.
Например: 1;15;36;12356.
Рассмотрим значение 15 — целое число со знаком плюс, то есть положительное значение. На координатной прямой оно располагается справа от нулевого значения или точки первоначального отсчета.
Определение
Отрицательное число — данное определение идентично вышеуказанному положительному, за исключение левой стороны от нулевого значения и знак меняется с плюса на минус.
Примеры целых отрицательных чисел: − 52, − 258, − 1 -528, -2568, -1. Нулевое значение делит между собой положительные и отрицательные целые числа. В то же время оно является ни положительным и ни отрицательным. Числовое значение, которое является обратным каждому отрицательному значению, следовательно, является положительным целым числом.
Сравнивая с нулевым значением, можно сформулировать и другие определения, конкретно опираясь на ноль.
Например: числа, которые являются меньше нуля, можно назвать отрицательными целыми числовыми значениями.
Числа, которые больше нулевого данного числа, будет называться простыми положительными значениями.
Положительные данные, находящиеся правее от нулевого числового значения, следовательно, отрицательные мы увидим слева от нуля.
Мы уже рассмотрели и изучили правило, что натуральные числа — это целый ряд или подмножество целых значений. Рассмотрим это подробнее.
Несколько данных натуральных чисел объединяют в себя целые положительные значения. Из этого следует, что множество отрицательных целых значений числа, может быть представлено, как множество значений, с обратным значением знака к натуральным числам.
Стоит уделить внимание следующему понятию — любое натуральное число значение, может иметь свойство целого значения, однако, не каждое целое значение может быть натуральным. Дадим определения таким значениям как, неотрицательные и неположительные:
Дадим определения таким значениям как, неотрицательные и неположительные:
- Неотрицательные целые числа — это положительные числа и нулевое числовое значение.
- Неположительные целые числа — это отрицательные целые числа и значение равное нулю.
Как мы уже говорили ранее числовое данное равное нулю, не относится ни к какому из изученных натуральных значений.
Простыми примерами неотрицательных чисел могут быть следующие значения: 45; 142; 26589;105689.
В свою очередь -52; -5698; -12598 это неположительные значения.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Нужна помощь
Как пишется знак больше меньше в математике
Знаки «больше (>)» или «меньше (<)» обычно используются для отображения отношений между числами. Они позволяют продемонстрировать, какое число имеет большее или меньшее значение, и применяются с целью помочь учащимся разобраться с соотношениями чисел. Знаки «больше» или «меньше» также часто известны как знаки «больше чем» и «меньше чем».
Широкий конец данного знака всегда обращён к большему числу. Например:
25 > 10
100 > 50
500 > 200
Знак «больше» (>) означает, что число перед знаком «больше» всегда больше числа, которое находится после данного знака.
200 > 100
Знак меньше (<) означает, что число перед данным знаком всегда меньше, нежели число после данного знака. Как видим, визуально знак «больше» и «меньше» — это просто перевернутые версии одного и того же символа.
100 < 200
Знак равенства (=) означает, что число после знака равно числу перед знаком.
Важно! Знак равенства не является показателем результата работы над числами (например, 3+5=8). Данный знак показывает, что сумма чисел слева равна сумме чисел справа
То есть 3+5 слева равно числу справа, которым и является 8.
Когда же два значения определенно не равны, тогда мы используем пример со знаком «не равно»: 2+2 ≠ 9. То есть сумма значений чисел слева (4) не равно значению чисел справа (9).
Определение нулевых чисел и их важность
Нулевые числа — это числа, которые имеют значение 0. Они являются особыми числами в математике и играют важную роль в различных областях науки и практической деятельности.
Нулевые числа считаются обычно исключительными, потому что они не имеют значения в обычном смысле. Однако, без нулевых чисел многие математические и физические концепции были бы неполными или даже невозможными.
Вот несколько примеров, демонстрирующих важность нулевых чисел:
Символическое обозначение: Ноль является символическим обозначением для отсутствия или пустоты
Он используется для обозначения нулевой суммы, нулевого количества или нулевой степени в различных математических операциях и формулах.
Место-значимость: Ноль имеет важное значение в позиционной системе счисления, такой как десятичная система. Он помогает определять место-значение других цифр и расширяет диапазон представления чисел
Графики и функции: Нулевые числа играют важную роль в построении графиков и решении уравнений
Они помогают определить точки пересечения графиков, корни уравнений и решения систем уравнений.
Физические законы: Многие физические законы и формулы включают нулевые значения. Например, закон сохранения энергии или закон Второго начала термодинамики связаны с отсутствием энергии или изменениями энтропии.
Все эти примеры показывают, что нулевые числа не являются просто ничтожными или бесполезными. Они играют роль основных элементов в математике, науке и повседневной жизни, и их понимание является важным для достижения точности, логического мышления и аналитических навыков.
Топ вопросов за вчера в категории Математика
Математика 21.06.2023 06:59 942 Тупиков Сергей.
Запишите в десятичной записи число: а) 74; б) 350; в)636300; г)2800005.
Ответов: 1
Математика 15.06.2023 02:27 528 Журавель Настя.
Велосипед ехал 2,6 ч со скоростью 6,6 м/с,а затем 1,4 ч со скоростью 5,2 м/с.чему равна средняя скор
Ответов: 2
Математика 04.06.2023 14:00 561 Матвеева Лиля.
Запишите в десятичной записи число: а) 74, б) 350, в) 636 300 г) два миллиона восемьсот тысяч 5 д) 2
Ответов: 1
Математика 18.05.2023 04:51 875 Максимова Катя.
Найдите отношение длины диагонали листа формата а7 к его меньшей стороне ответ округлите до десятых
Ответов: 2
Математика 20.06.2023 17:50 190 Аветисян Карен.
Равны ли множества А и В А={1}, В=`1`
Ответов: 1
Математика 14.06.2023 02:36 237 Чиняев Глеб.
На одну порцию десерта из клубники берут 120г ягод и 25г сливок.Сколько сливок потребуется для приго
Ответов: 1
Математика 14.06.2023 11:22 399 Анфалова Татьяна.
Экскурсионный теплоход двигался 4,3 ч по озеру со скоростью 20км/ч, затем 2,5 ч по реке со скоростью
Ответов: 1
Математика 15.06.2023 03:21 285 Кулакова Лиза.
Найдите среднюю длину своего шага,измерив длину пяти своих шагов
Ответов: 1
Математика 21.06.2023 08:32 177 Верхозин Александр.
2. Сколько лошадей в двух табунах, если в одном табуне 836 лошадей, а в другом на 308 больше? 3.Вычи
Ответов: 2
Математика 18.07.2023 20:29 90 Филимонов Захар.
10A ДОМАШНЕЕ ЗАДАНИЕ Узнай из диаграммы количество мест в построенных школах по годам. Запиши эти
Ответов: 1
Примеры нулевых чисел в различных областях
-
Математика: В математике нулевое число обозначается символом «0» и является базовым элементом для арифметических операций. Например, 0 является нейтральным элементом для сложения и вычитания, а также представляет собой результат умножения числа на ноль.
-
Физика: В физике нуль используется для измерения относительных значений. Например, абсолютный ноль (-273.15°C) является нижней границей температуры, при которой молекулы прекращают движение.
-
Информатика: В программировании и компьютерных науках нулевое значение часто используется для обозначения отсутствия данных или недопустимого значения. Например, в строке кода число 0 может означать, что переменная не содержит никакого значения или что операция завершилась успешно.
-
Статистика: В статистике нуль часто используется для обозначения отсутствия или неточности данных. Например, нулевой показатель может указывать на отсутствие событий или нулевую вероятность их возникновения.
-
Лингвистика: В лингвистике нуль может использоваться, например, в контексте нулевого артикля. Он указывает на отсутствие определенного артикля в некоторых случаях, например, при обозначении общих понятий.
Это лишь некоторые примеры, как нулевые числа используются в различных областях знаний. В каждом случае нуль может иметь свою специфическую интерпретацию и значение, связанное с конкретным контекстом.
Обзор терминологии в других словарях по математике
В математике существует несколько способов описания отношения «больше» и «меньше» между числами. В задачах, где не требуется строгое сравнение, можно использовать нестрогие неравенства ≤ (меньше или равно) и ≥ (больше или равно). Другими словами, если одно число не меньше или не больше другого, то эти числа равны.
В некоторых словарях по математике используются арифметические знаки «» (больше) для обозначения отношений между числами. В этом случае символ «» — перед большим числом. Например, условие «7
В математических досках или картинках доски могут использоваться числовые типы «меньше» и «больше», чтобы задачу решить быстрого. Например, в задаче «Какой из двух чисел больше: 5 или 10?» на доске может быть нарисовано несколько кубиков, где одна сторона имеет числовое выражение «5», а другая сторона — «10». Ребра, соединяющие эти стороны, будут показывать, что число 10 больше числа 5.
В словарях также могут использоваться слова «больше» и «меньше». Например, в «словаре крокодил» задачи #51″ используются термины «больше» и «меньше» для сравнения чисел. В этой игре карточки с числами располагаются в случайном порядке на столе, и игрокам нужно определить, какое число больше или меньше других чисел.
Значение выражения не менее в математике: что означает больше или меньше? Статья
Contents
Таблица математических символов
В математике символы используются повсеместно для упрощения и сокращения текста. Здесь перечислены наиболее распространенные математические символы, соответствующие им команды TEX, описания и примеры их использования.
В дополнение к вышеперечисленным значкам можно использовать зеркальные изображения символов, например.
Символы актов или математические символы — это символы, которые символизируют конкретный математический акт в аргументе.
Математическая таблица символов, таблица символов, таблица символов ASCII, таблица символов HTML, таблица кодов HTML, таблица символов WordPress, таблица символов ников, таблица символов на клавиатуре, таблица символов клавиатуры WK
Таблица математических символов что, таблица математических символов кто, таблица математических символов


























