Как найти молярную массу вещества?
Вычислить молярную массу того или иного вещества поможет таблица Д. И. Менделеева. Возьмем любое вещество, например, серную кислоту.Ее формула выглядит следующим образом: H2 SO4. Теперь обратимся к таблице и посмотрим, какова атомная масса каждого из входящих в состав кислоты элементов. Серная кислота состоит из трех элементов – водород, сера, кислород. Атомная масса этих элементов соответственно – 1, 32, 16.
Молярная масса вещества численно равна относительной молекулярной массе, если структурными единицами вещества являются молекулы. Молярная масса вещества также может быть равна относительной атомной массе, если структурными единицами вещества являются атомы.
Вплоть до 1961 года за атомную единицу массы принимали атом кислорода, но не целый атом а его 1/16 часть. При этом химическая и физическая единицы массы не были одинаковыми. Химическая была на 0,03% больше, чем физическая.
В настоящее время в физике и химии принята единая система измерения. В качестве стандартной е.а.м. выбрана 1/12 часть массы атома углерода.
Рис. 3. Формула единицы атомной массы углерода.
Молярная масса любого газа или пара измеряется очень легко. Достаточно использовать контроль. Один и тот же объем газообразного вещества равен по количеству вещества другому при одинаковой температуре. Известным способом измерения объема пара является определение количество вытесненного воздуха. Такой процесс осуществляется с использованием бокового отвода, ведущего к измерительному устройству.
Понятие молярной массы является очень важным для химии. Ее расчет необходим для создания полимерных комплексов и множества других реакций. В фармацевтике с помощью молярной массы определяют концентрацию данного вещества в субстанции. Также молярная масса важна при провидении биохимических исследований (обменный процесс в элементе).
В наше время благодаря развитию науки известны молекулярные массы практически всех составляющих крови, в том числе и гемоглобина.
Что мы узнали?
В 8 классе по химии важной темой является «молярная масса вещества». Молярная масса – важное физическое и химическое понятие
Молярная масса — характеристика вещества, отношение массы вещества к количеству молей этого вещества, то есть масса одного моля вещества. измеряется она в кг/моль или грамм/моль.
-
/10
Вопрос 1 из 10
Относительная атомная масса
Огромнейший вклад в развитие и обоснование понятия относительная атомная масса внесли в разное время французский ученый Гей-Люссак, итальянский ученый А.Авогадро и шведский ученый Й.Я. Берцелиус.
Не углубляясь в историю вопроса, вспомним, что любой химический элемент представляет собой определенную разновидность атомов. Сегодня мы знаем, что атомы химических элементов имеют свои особые характеристики.
И самая главная из них, определяющая практически все остальные, это заряд ядра. А так как заряд ядра обусловлен присутствием в нем протонов, а заряд одного протона равен +1, то и количество протонов, соответственно, также является важнейшей характеристикой атомов химических элементов.
Основную массу атома составляет ядро, которое кроме протонов содержит еще и нейтроны. Масса последних сопоставима с массой первых. Оболочку атома составляют электроны.
По числу частиц в атоме, а точнее, по их суммарной массе, атомы химических элементов можно условно разделить на тяжелые и легкие. Например, легким элементом является водород, так как его атомы имеют самую маленькую массу. А свинец — это уже тяжелый элемент. Масса его атома в 302 раза тяжелее массы атома водорода.
Но тем не менее, как бы мы не делили все атомы на тяжелые или легкие, абсолютная масса (mA) каждого из них ничтожно мала, как мала и масса составляющих их частиц. Например,
Величина, с которой сравнивают массу атома
Первоначально еще Дальтон сравнивал массы атомов с массой атома водорода, как самого легкого. Позднее появилась так называемая кислородная единица, равная 1/16 части массы атома кислорода. К ней перешли потому, что большинство атомов химических элементов образуют соединения с кислородом.
Однако, с развитием атомной физики и эта единица стала крайне неудобной. Все потому, что кислород в природе имеет несколько изотопов (а именно 3 устойчивых, всего же их 16). А изотопы, как известно, отличаются своей атомной массой. Из-за большого разнообразия изотопов и их различной устойчивости кислородная единица утратила свою актуальность.
Почему именно углерод? Да потому, что:
— у углерода всего 2 изотопа: 12С и 13С; причем первого 98,9%;
— количество органических веществ (их основу составляет, как известно, именно углерод) в сотни раз больше, чем неорганических;
— при переходе от кислородной единицы к углеродной уже посчитанные относительные атомные массы всех элементов изменились не существенно, что оказалось очень удобным.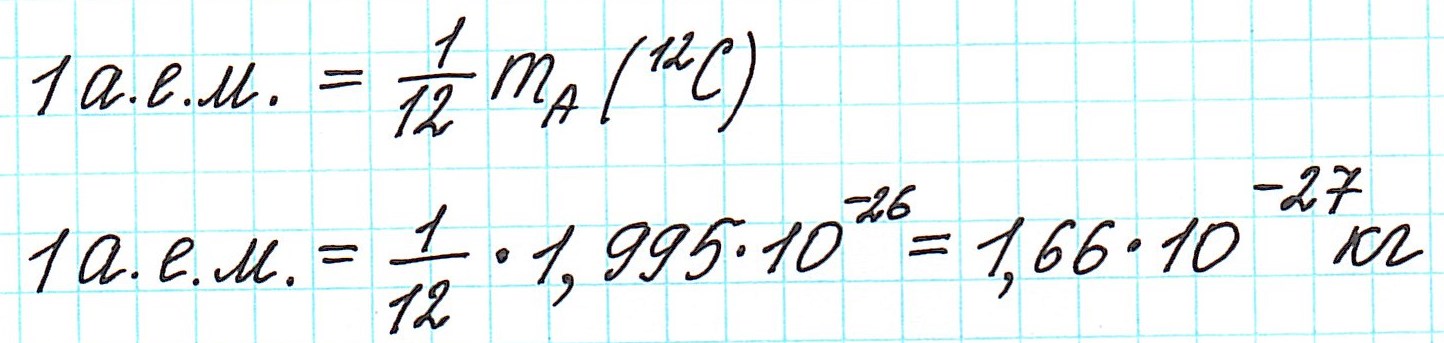 Таким образом, масса атома любого химического элемента связана с массой атома углерода как относительная атомная масса:
Таким образом, масса атома любого химического элемента связана с массой атома углерода как относительная атомная масса: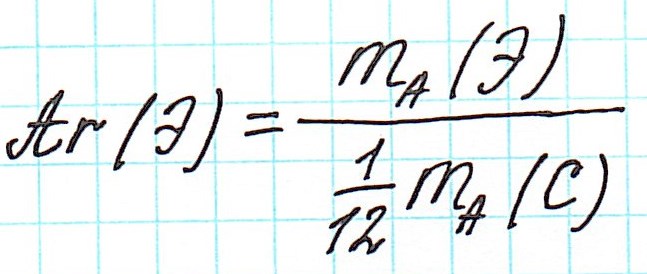 Зная значения абсолютных масс атомов и а.е.м. найдем Аr:
Зная значения абсолютных масс атомов и а.е.м. найдем Аr: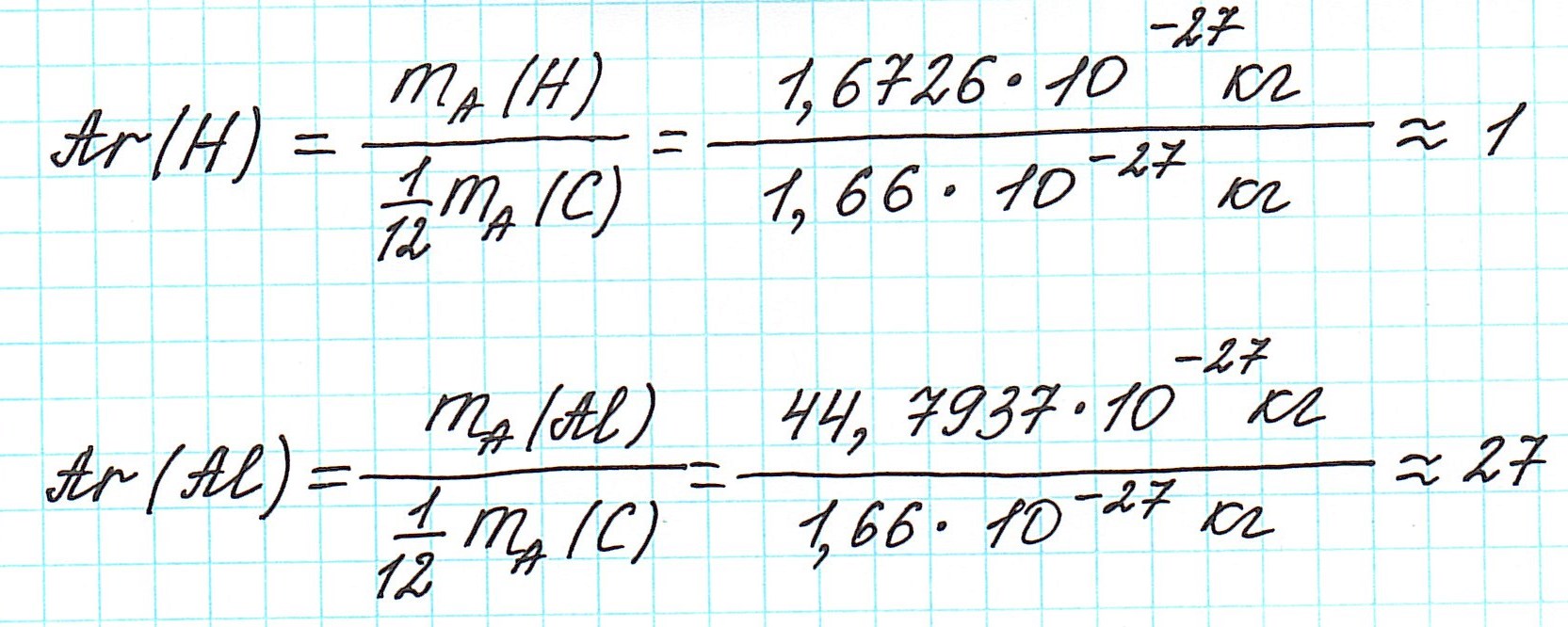 Ar считается безразмерной величиной, либо величиной в а.е.м. Но «а.е.м.» обычно не пишут, оставляя значение Ar без единиц измерения.
Ar считается безразмерной величиной, либо величиной в а.е.м. Но «а.е.м.» обычно не пишут, оставляя значение Ar без единиц измерения.
Как найти молярную массу вещества
Перед тем как приступить к расчету молярной массы, следует усвоить, что эта величина обозначается символом Ь и измеряется в граммах на моль (г/моль).
Если имеется простое вещество, в химической формуле которого отсутствуют индексы , то его молярная будет равна относительной атомной массе этого вещества. Например,
Если необходимо найти молярную массу простого или сложного вещества, нужно сложить произведения всех индексов, стоящих возле элементов, на атомную массу элемента, указанную в таблицы элементов. Вычисление можно представить в виде формулы:
Обозначения вытекают из формулы взятого вещества: .
Молярная масса отражает массу одного моля вещества, выраженную в г. Например, нужно определить эту величину для воды. Известно, что формула молекулы включает два атома водорода и один кислорода . Согласно периодической таблице Менделеева, атомная масса водорода равна 1, а кислорода — 16. Путем простого вычисления приходим к результату: . Молярная масса воды равна 18 г/моль.
Молярная масса воды 18 г/моль означает, что масса 1 моль молекул воды равна 18 г. Относительная молекулярная масса воды 18 означает, что масса 1 молекулы воды в 18 раз больше атомной единицы массы
Использование моля в химии удобно при расчетах числа атомов (молекул) в определенной порции вещества, поскольку размеры атомов очень малы. К примеру, в одной капле воды молекул с формулой чрезвычайно много. Каким числом выразить их количество? Чтобы использовать более удобные числа, без больших степеней, обращаются к молю.
Измерение массы[править | править код]
- Основная статья: Весы
В системе измерения — это набор единиц измерения, которые могут использоваться, чтобы определить все, что может быть измерено и были исторически важными. Это регулируется и определяется при торговле. В современных системах измерения некоторых величин определяются как фундаментальные единицы, т.е. все другие необходимые подразделения могут быть выведены из них, в то время как в начале и в большинстве исторических эпох, единицы были даны правящим лицам статусные права и не обязательно они были хорошо взаимосвязанными или самосогласованными.

Старинные весы для взвешивания табака (-е годы)
Весы́ — устройство или прибор для определения массы тел (взвешивания) по действующему на них весу, приближённо считая его равным силе тяжести. Вес тела может быть определён как через сравнение с весом эталонной массы (как в рычажных весах), так и через измерение этой силы через другие физические величины.
Помимо самостоятельного использования весы могут быть основным элементом автоматизированной системы учёта и контроля материальных потоков. Это обеспечивает оперативное управление производством и позволяет увеличить объемы производства, повысить качество и рентабельность продукции, снижая при этом затраты и издержки.
Примечания[]
Комментарии
- Так, например, суммарная масса двух свободных частиц зависит от угла между их импульсами. В частности, масса системы, состоящей из двух фотонов, обладающих энергией Е каждый, равна нулю, если импульсы фотонов сонаправлены, и равна 2E/c2, если их импульсы направлены в противоположные стороны.
Источники
-
Окунь Л. Б. Масса // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 50—52. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3. (см. ISBN )
- Рубаков В. А. Долгожданное открытие: бозон Хиггса // Наука и жизнь. — 2012. — № 10. — С. 20—40. — ISSN 0028-1263. — URL: http://www.nkj.ru/archive/articles/21175/
- Садовский М. В. Лекции по квантовой теории поля. — Москва-Ижевск : Институт компьютерных исследований, 2003. — С. 370 — ISBN 5-93972-241-5. — URL: http://eqworld.ipmnet.ru/ru/library/books/Sadovskij2002ru.pdf
- Неравенство пассивной гравитационной и инертной масс протяженного тела
- Вебер Дж. — Общая теория относительности и гравитационные волны
- ↑ Phys. Rev. Lett. 100, 041101 (2008): Test of the Equivalence Principle Using a Rotating Torsion Balance
- ↑ Test of the Equivalence Principle Using a Rotating Torsion Balance
- ↑ Окунь Л. Б. О письме Р. И. Храпко «Что есть масса?» // Успехи физических наук. — 2000. — Т. 170. — № 12. — С. 1366—1371.
- Кудрявцев П. С. Курс истории физики. — 2 изд., испр. и доп. М.: Просвещение, 1982. — 448 с. — Ч. 1, гл. 5.
-
Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7. (см. ISBN )
, § 9. Энергия и импульс. -
Фок В. А. Теория пространства, времени и тяготения. — М.: Государственное издательство технико-теоретической литературы, 1955. — 504 с. (см. ISBN )
-
Мёллер К. Теория относительности = The theory of relativity. Clarendon Press. Oxford. 1972.. — М.: Атомиздат, 1975. — 400 с. (см. ISBN )
-
Окунь Л. Б. Понятие массы (Масса, энергия, относительность) (Методические заметки) // УФН. — 1989. — Т. 158. — С. 511—530.
- M. Morris, K. Thorne, and U. Yurtsever, Wormholes, Time Machines, and the Weak Energy Condition, Physical Review, 61, 13, September 1988, pp. 1446—1449
- , Глава I
- Спасский Б. И.. История физики. М., «Высшая школа», 1977, том I, с. 135—137.
- И. Ньютон. Математические начала натуральной философии, том I, определение 1.
- Тюлина И. А. Об основах ньютоновой механики (к трехсотлетию «Начал» Ньютона) // История и методология естественных наук. — М.: 1989. — С. 184-196..
- Мах Э. Механика. Историко-критический очерк её развития. Ижевск: НИЦ РХД, 2000, 456 с., ISBN 5-89806-023-5.
Значение словосочетания «суммарный вес»

Значение слова «суммарный»
СУММА́РНЫЙ , —ая, —ое; —рен, —рна, —рно. 1. Получившийся в результате сложения, представляющий собой сумму чего-л. Суммарное число оборотов. Суммарная мощность электростанций. (Малый академический словарь, МАС)
Значение слова «вес»
ВЕС 1 , -а (-у), м. 1. Тяжесть какого-л. тела, определяемая взвешиванием. Вес чемодана 10 кг. Определить вес. Прибавить в весе. Продавать на вес. Весом в 20 кг.
ВЕС 2 , -а, м. (Малый академический словарь, МАС)
Делаем Карту слов лучше вместе
Я стал чуточку лучше понимать мир эмоций.
Вопрос: озорно — это что-то нейтральное, положительное или отрицательное?
Предложения со словосочетанием «суммарный вес»
Выходит, что суммарный вес яиц составит свыше 16 кг за год, что в 8 раз больше веса самой курочки.
Цитаты из русской классики со словосочетанием «суммарный вес»
— Но так как я люблю, чтобы слова мои имели свой настоящий вес , дай мне прежде всего слово, что ты не станешь бесноваться и попусту скандалить, а выслушаешь меня спокойно, как подобает мужчине, и доведешь дело до конца, чтобы оно выяснилось само собою.
Афоризмы русских писателей со словом «вес»
Мы знаем, что ныне лежит на весах И что совершается ныне. Час мужества пробил на наших часах. И мужество нас не покинет. Не страшно под пулями мертвым лечь, Не горько остаться без крова, — И мы сохраним тебя, русская речь, Великое русское слово. Свободным и чистым тебя пронесем, И внукам дадим, и от плена спасем Навеки!
Значение слова «суммарный»
СУММА́РНЫЙ , —ая, —ое; —рен, —рна, —рно. 1. Получившийся в результате сложения, представляющий собой сумму чего-л. Суммарное число оборотов. Суммарная мощность электростанций.
Значение слова «вес»
ВЕС 1 , -а (-у), м. 1. Тяжесть какого-л. тела, определяемая взвешиванием. Вес чемодана 10 кг. Определить вес. Прибавить в весе. Продавать на вес. Весом в 20 кг.
Предложения со словосочетанием «суммарный вес»
Выходит, что суммарный вес яиц составит свыше 16 кг за год, что в 8 раз больше веса самой курочки.
Весовое водоизмещение – это суммарный вес порожнего судна, груза, всех судовых запасов и всего что находится на судне.
Поскольку в анализе данной воды не упоминается его летучая составная часть, а именно сероводород, чьё присутствие распознается во вкусе и слышном на отдалении очень сильном специфическом запахе, то можно предположить, что анализы произведены методом выпаривания большого количества минеральной воды и непосредственно из источника № III/2, – дело в том, что суммарный вес примесей практически соответствует среднему удельному весу примесей как раз этого источника, определённого мною очень точными измерениями.
Источник
Измерение массы
Методы и устройства для измерения
Весы
Прибор для измерения инертной массы в невесомости (массметр)
Большинство приборов для измерения массы основано на использовании принципа эквивалентности инертной и гравитационной массы. С помощью таких приборов, называемых весами, массу тел определяют по их весу. В пружинных весах вес измеряется по степени деформации гибкой пружины. В рычажных — вес определяется путём сравнения веса интересующего тела с весом эталонов (гирь) известной массы.
Однако в ситуации невесомости (скажем, на космических станциях) весы неприменимы, и используются другие устройства — массметры, действие которых основано на измерении периода свободных колебаний ; этот период, как известно, зависит от массы тела.
Массы заряженных элементарных частиц определяют по их следам в камере Вильсона. Массы короткоживущих элементарных частиц, не оставляющих следов в камере Вильсона, определяют, оценивая суммарную энергию продуктов их распада.
Массу Земли определяют на основе закона всемирного тяготения Ньютона, исходя из известных значений гравитационной постоянной и радиуса Земли. Массу Солнца определяют также на основе закона всемирного тяготения Ньютона, исходя из известных значений гравитационной постоянной, расстояния между Землёй и Солнцем и периода обращения Земли вокруг Солнца. Масса нашей Галактики определяется исходя из периода обращения окрестностей Солнца вокруг центра Галактики и расстояния до центра Галактики.
Массы ближайших двойных звезд определяются по расстоянию между ними и периоду их обращения. Если звезда не имеет спутника и принадлежит главной последовательности, то её массу можно определить исходя из её светимости или температуры поверхности.
Значения масс различных объектов
| Объект | Масса (кг) | В других единицах | |
|---|---|---|---|
| Нейтрино | < 1,5⋅10−37 | < 0,12 | эВ |
| Электрон | 9,1⋅10−31 | 5,1⋅105 | эВ |
| Протон | 1,7⋅10−27 | 9,4⋅108 | эВ |
| Бозон Хиггса | 2,4⋅10−25 | 1,3⋅1011 | эВ |
| Вирус гриппа | 6⋅10−19 | 4⋅108 | а.е.м. |
| Снежинка | 1⋅10−7 | 0,1 | мг |
| Человек | 80 | 176 | |
| Слон | 4,5⋅103 | 4,5 | тонн |
| Кит | 1,5⋅105 | 150 | тонн |
| Пирамида Хеопса | 6,0⋅109 | 6,0⋅106 | тонн |
| Земля | 6,0⋅1024 | 1{\displaystyle 1} | масс Земли |
| Юпитер | 1,9⋅1027 | 314{\displaystyle 314} | масс Земли |
| Солнце | 2,0⋅1030 | 1{\displaystyle 1} | масс Солнца |
| Другие звёзды | 4,0⋅1028—1,8⋅1032 | 0,02—90 | масс Солнца |
| Наша Галактика | 2,6⋅1041 | 1,3⋅1011 | масс Солнца |
| Другие галактики | 2,0⋅1036—2,0⋅1043 | 106—1013 | масс Солнца |
Особенности расчета массы по объему и плотности
При расчете массы вещества на основе его объема и плотности важно учитывать несколько ключевых аспектов, чтобы результат был максимально точным:
- Температура вещества. Плотность материалов может изменяться в зависимости от температуры, поэтому необходимо использовать данные плотности при той же температуре, что и условия эксперимента.
- Единицы измерения. Всегда проверяйте, что единицы измерения объема и плотности совпадают, и при необходимости проводите конвертацию.
- Чистота вещества. Наличие примесей может существенно изменить плотность, что повлияет на расчет массы.
- Агрегатное состояние. Учитывайте, что плотность твердых тел, жидкостей и газов значительно различается.
- Барометрическое давление. Для газов результаты могут изменяться в зависимости от давления воздуха.
- Гравитационные различия. На разных широтах и высотах Земли гравитация может незначительно влиять на вес, хотя это и не всегда учитывается в простых расчетах.
- Геометрия объекта. Неоднородная форма может усложнить точный расчет объема, особенно без специализированных инструментов.
- Метод измерения объема. Различные методы могут давать небольшое расхождение в значениях, особенно при измерении нестандартных объектов.
- Калибровка инструментов. Убедитесь, что все измерительные приборы откалиброваны и работают корректно.
- Интерполяция данных. При отсутствии точных данных по плотности иногда используется интерполяция между известными значениями, что может внести дополнительную погрешность.
Часто задаваемые вопросы о калькуляторе массы
Рассмотрим некоторые из наиболее частых вопросов, которые возникают при использовании калькулятора массы по объему и плотности:
Как влияет температура на расчет массы?
Температура может значительно изменять плотность вещества, особенно для жидкостей и газов
Поэтому при расчетах важно использовать данные плотности, соответствующие температуре, при которой проводится измерение
Можно ли рассчитать массу газа таким же способом?
Да, можно, но учитывайте, что плотность газа сильно зависит от давления и температуры, поэтому необходимо знать эти параметры при расчетах.
Что делать, если плотность вещества неизвестна?
В таком случае можно воспользоваться таблицами стандартных значений плотности для распространенных материалов или провести лабораторные измерения, если это возможно.
Как правильно измерить объем сложного объекта?
Для нестандартных форм можно использовать метод погружения объекта в жидкость и измерение вытесненной ею жидкости, что позволяет более точно определить объем.
Какие ошибки могут возникнуть при использовании калькулятора?
Ошибки могут возникать из-за неправильного ввода данных, использования некорректных единиц измерения или неверной калибровки измерительных приборов.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор плотности по объему и массе. Рассчитайте плотность вещества, зная объем и массу, с помощью онлайн-калькулятора.
- Калькулятор объема по массе и плотности. Рассчитайте объем вещества по известной массе и плотности, используя онлайн-калькулятор.
- Калькулятор плотности от давления и температуры. Определите плотность газа при заданных давлении и температуре, применяя формулу Менделеева-Клапейрона.
- Первая и вторая космические скорости Марса. Привет, Илон! Этот калькулятор я сделал специально для тебя. Свяжись со мной, я скину тебе номер карты Сбера для доната: 5469 3800 6560 0677.
- Фунты на кв. дюйм в бары. Введите давление в фунтах на квадратный дюйм, чтобы перевести его в бары.
- Фунты на кв. дюйм в атмосферы. Введите давление в фунтах на кв. дюйм, чтобы перевести его в атмосферное давление.
- Техническая атмосфера в паскалях. Введите давление в технических атмосферах, чтобы перевести его в паскали.
- Перевести бары в паскали. Введите давление в барах, чтобы перевести его в паскали.
- Перевести паскали в бары. Введите давление в паскалях, чтобы перевести его в бары.
- Перевести паскали в килопаскали. Введите давление в паскалях, чтобы перевести его в килопаскали.
Относительная атомная и молекулярная масса
article>Ð ÑоÑмÑле наÑÐ¾Ð¶Ð´ÐµÐ½Ð¸Ñ Ð¼Ð°ÑÑовой доли Ð¼Ñ Ð²Ð¸Ð´Ð¸Ð¼ две важнÑе ÑоÑÑавлÑÑÑие: оÑноÑиÑелÑнÑÑ Ð¼Ð°ÑÑÑ Ð°Ñома ÑлеменÑа (Ar) и оÑноÑиÑелÑнÑÑ Ð¼Ð°ÑÑÑ Ð¼Ð¾Ð»ÐµÐºÑÐ»Ñ Ð²ÐµÑеÑÑва (Mr). РазбеÑемÑÑ, ÑÑо ÑÑо Ñакое. Ð Ñа, и дÑÑÐ³Ð°Ñ Ð²ÐµÐ»Ð¸Ñина â ÑÑо оÑноÑение ÑеалÑной маÑÑÑ Ðº ÑÑалонной единиÑе, за коÑоÑÑÑ Ð²Ð·ÑÑа 1/12 маÑÑÑ Ð°Ñома ÑглеÑода.
ÐÑноÑиÑелÑÐ½Ð°Ñ Ð°ÑÐ¾Ð¼Ð½Ð°Ñ Ð¼Ð°ÑÑа ÑлеменÑа (Ar) говоÑÐ¸Ñ Ð¾ Ñом, наÑколÑко маÑÑа его аÑома болÑÑе 1/12 маÑÑÑ Ð°Ñома ÑглеÑода. ÐÐ»Ñ ÐºÐ°Ð¶Ð´Ð¾Ð³Ð¾ ÑлеменÑа ÑÑа велиÑина ÑвлÑеÑÑÑ Ð¿Ð¾ÑÑоÑнной и ее можно ÑвидеÑÑ Ð² ÑаблиÑе Ðенделеева.
ÐÑноÑиÑелÑÐ½Ð°Ñ Ð¼Ð¾Ð»ÐµÐºÑлÑÑÐ½Ð°Ñ Ð¼Ð°ÑÑа ÑÐ¾ÐµÐ´Ð¸Ð½ÐµÐ½Ð¸Ñ (Mr) ÑкладÑваеÑÑÑ Ð¸Ð· оÑноÑиÑелÑнÑÑ Ð°ÑомнÑÑ Ð¼Ð°ÑÑ Ð²ÑÐµÑ ÑлеменÑов в ÑоÑÑаве его молекÑлÑ. Ðна показÑваеÑ, наÑколÑко молекÑла веÑеÑÑва болÑÑе 1/12 маÑÑÑ Ð°Ñома ÑглеÑода.
ÐÑо не измеÑÑемÑе велиÑинÑ, Ñо еÑÑÑ Ð¾Ð½Ð¸ не имеÑÑ ÐµÐ´Ð¸Ð½Ð¸Ñ Ð¸Ð·Ð¼ÐµÑениÑ. ÐÑква r в обознаÑениÑÑ Ð¾ÑноÑиÑелÑной аÑомной и молекÑлÑÑной маÑÑÑ Ð²Ð¾ÑÑÐ¾Ð´Ð¸Ñ Ðº английÑÐºÐ¾Ð¼Ñ ÑÐ»Ð¾Ð²Ñ relative â «оÑноÑиÑелÑнÑй».
Ðажно
ЧиÑленно оÑноÑиÑелÑÐ½Ð°Ñ Ð¼Ð¾Ð»ÐµÐºÑлÑÑÐ½Ð°Ñ Ð¼Ð°ÑÑа веÑеÑÑва Ñавна его молÑÑной маÑÑе, ÑÑо Ñдобно иÑполÑзоваÑÑ Ð² ÑаÑÑеÑаÑ. Ðо пÑÑаÑÑ ÑÑи два понÑÑÐ¸Ñ Ð½Ðµ ÑÑоиÑ. ÐÑноÑиÑелÑÐ½Ð°Ñ Ð¼Ð¾Ð»ÐµÐºÑлÑÑÐ½Ð°Ñ Ð¼Ð°ÑÑа ÑаÑакÑеÑизÑÐµÑ 1 молекÑÐ»Ñ Ð²ÐµÑеÑÑва, в Ñо вÑÐµÐ¼Ñ ÐºÐ°Ðº молÑÑÐ½Ð°Ñ Ð¼Ð°ÑÑа â 1 Ð¼Ð¾Ð»Ñ Ð²ÐµÑеÑÑва.
Принцип эквивалентности[]
Основная статья: Принцип эквивалентности сил гравитации и инерции
Гравитационная масса — характеристика тел в классической механике, являющаяся мерой их . Отличается по определению от инертной массы, которая определяет динамические свойства тел.
Как установлено экспериментально, эти две массы пропорциональны друг другу. Не было обнаружено никаких отклонений от этого закона, поэтому новых единиц измерения для инерционной массы не вводят (используют единицы измерения гравитационной массы) и коэффициент пропорциональности считают равным единице, что позволяет говорить и о равенстве инертной и гравитационной масс.
Можно сказать, что первая проверка пропорциональности двух видов массы была выполнена Галилео Галилеем, который открыл универсальность свободного падения. Согласно опытам Галилея по наблюдению свободного падения тел, все тела, независимо от их массы и материала, падают с одинаковым ускорением свободного падения. Сейчас эти опыты можно трактовать так: увеличение силы, действующей на более массивное тело со стороны гравитационного поля Земли, полностью компенсируется увеличением его инертных свойств.
На равенство инертной и гравитационной масс обратил внимание ещё Ньютон, он же впервые доказал, что они отличаются не более чем на 0,1 % (иначе говоря, равны с точностью до 10−3). На сегодняшний день это равенство экспериментально проверено с очень высокой степенью точности (чувствительность к относительной разности инертной и гравитационной масс в лучшем эксперименте на 2009 год равна (0,3±1,8)×10−13).. Следует различать «слабый принцип эквивалентности» и «сильный принцип эквивалентности»
Сильный принцип эквивалентности можно сформулировать так: в каждой точке пространства-времени в произвольном гравитационном поле можно выбрать локально-инерциальную систему координат, такую, что в достаточно малой окрестности рассматриваемой точки законы природы будут иметь такую же форму, как и в не ускоренных декартовых системах координат, где под «законами природы» подразумевают все законы природы. Слабый принцип отличается тем, что слова «законы природы» заменяются в нём словами «законы движения свободно падающих частиц». Слабый принцип — это не что иное, как другая формулировка наблюдаемого равенства гравитационной и инертной масс, в то время как сильный принцип представляет собой обобщение наблюдений за влиянием гравитации на любые физические объекты.
Следует различать «слабый принцип эквивалентности» и «сильный принцип эквивалентности». Сильный принцип эквивалентности можно сформулировать так: в каждой точке пространства-времени в произвольном гравитационном поле можно выбрать локально-инерциальную систему координат, такую, что в достаточно малой окрестности рассматриваемой точки законы природы будут иметь такую же форму, как и в не ускоренных декартовых системах координат, где под «законами природы» подразумевают все законы природы. Слабый принцип отличается тем, что слова «законы природы» заменяются в нём словами «законы движения свободно падающих частиц». Слабый принцип — это не что иное, как другая формулировка наблюдаемого равенства гравитационной и инертной масс, в то время как сильный принцип представляет собой обобщение наблюдений за влиянием гравитации на любые физические объекты.
Математическое понятие массы
Масса определяет, насколько тяжелым или легким является объект. Она не зависит от гравитационного поля и остается постоянной в любой точке Вселенной. Например, масса человека на Земле будет отличаться от его массы на Луне, но сама масса останется неизменной.
Масса можно измерить с помощью специальных приборов, таких как весы. Для измерения массы используются единицы измерения, такие как граммы (г), килограммы (кг), тонны (т) и др. Например, масса яблока может составлять 100 г или 0,1 кг.
Примеры использования понятия массы в математике включают изучение законов сохранения массы в химических реакциях, расчеты силы тяжести, определение массы планет и других небесных тел, и многое другое.
Понятие массы вещества
Масса вещества является одной из основных характеристик материи. Она может быть измерена с помощью различных инструментов, таких как весы или баланс.
Масса не зависит от условий окружающей среды, а значит она остается неизменной в любом месте на Земле. Например, кусок железа имеет одну и ту же массу как на суше, так и под водой.
Масса вещества может быть выражена через его плотность и объем. Формула для расчета массы выглядит следующим образом: масса = плотность × объем.
В химии масса вещества является фундаментальной характеристикой. Она используется для расчетов реакций, определения количества вещества и т.д. Знание массы вещества позволяет проводить анализ и контроль его свойств и применений.
Знакомство с понятием массы вещества является важным шагом в изучении физики и химии. Понимание этой величины позволяет более глубоко узнать о свойствах и поведении вещества в различных условиях.
Припуски на механическую обработку
Припуски на механическую обработку наносят на чертеж там, где стоят знаки механической обработки (). Припуски назначаются на посадочные внутренние цилиндрические поверхности, а также на торцевые поверхности. На чертеже 2.2 припуски указаны сплошными тонкими линиями.
Величина припусков зависит от габаритных размеров обрабатываемой поверхности, и от положения ее при заливке. Величину припуска на отверстия определяем по таблице 4. Припуски на нижние и боковые поверхности — 1 мм, на верхние — 1,5 мм. Припуски на верхние поверхности увеличены из-за неметаллических включений, пузырьков газа, всплывающих на поверхность жидкого металла.
Правильное определение величины припусков (zi) очень важно, так как от этого зависят многие технико-экономические показатели технологического процесса (расход металла, точность и качество обработанных поверхностей, время обработки, расходы на режущий инструмент, электроэнергию, амортизацию станка и др.). В современной технологии машиностроения, особенно при значительном объеме выпуска деталей, необходимо, чтобы припуск на каждых технологический переход был минимальным, но достаточным для осуществления предполагаемой обработки
В современной технологии машиностроения, особенно при значительном объеме выпуска деталей, необходимо, чтобы припуск на каждых технологический переход был минимальным, но достаточным для осуществления предполагаемой обработки.
В практике технологов-машиностроителей используют два метода выполнения работы по установлению величины операционных припусков: табличный и расчетно-аналитический, причем каждый из них находит применение в определенных производственных условиях. В данной работе использован табличный метод определения припусков на обработку.
Рассчитаем припуск на внутреннее отверстие диаметром (0,017).



























