Что такое система счисления
Система нумерации — это символьный метод записи чисел, представление чисел с помощью символов.
Символы, используемые для записи числа, называются цифрами.
- даёт представления множества чисел (целых или вещественных)
- даёт каждому числу уникальное представление (или, по крайней мере, стандартное представление)
- отражает алгебраическую и арифметическую структуру чисел.
Разные народы в разное время использовали разные системы нумерации. Следы древних систем счисления можно найти и сегодня в культурах многих народов. Вавилоняне восходят к делению часа на 60 минут и угла на 360 градусов. В Древнем Риме существовала традиция записывать числа I, II, III и т.д. в латинской нотации. Для англосаксов — измерение десятками: в году 12 месяцев, в футе 12 дюймов, день делится на 2 периода по 12 часов.
По современным данным, развитые системы нумерации впервые появились в Древнем Египте. Для записи чисел египтяне использовали иероглифы один, десять, сто, тысяча и т.д. Все остальные числа записывались с помощью этих иероглифов и акта сложения. Недостатками этой системы были невозможность записи больших чисел и ее неудобство.
В итоге десятичная система оказалась самой популярной системой счисления. Он состоит всего из 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, но информацию несет не только цифра, но и позиция, в которой она находится. В числе 444 три одинаковые цифры обозначают количество единиц, десятков и сотен. В числе 400, с другой стороны, первая цифра обозначает количество сотен. Два 0 сами по себе не вносят никакого вклада в число, а нужны только для того, чтобы указать положение цифры 4.
Классификация систем счисления
Системы нумерации делятся на позиционные и непозиционные.
Позиционные системы счисления
Позиционные системы нумерации (ПНС) — это системы нумерации, в которых количественный эквивалент каждой цифры (ее вес) зависит от ее положения в числе.
В ходе длительной эволюции человечество выработало позиционный принцип записи чисел, который заключается в том, что каждая цифра, содержащаяся в числовой записи, занимает определенную позицию, называемую разрядом. Цифры считаются справа налево. Каждая цифра всегда больше предыдущей на определенный коэффициент. Это отношение называется основанием системы счисления (в неположительных системах счисления термины «разряд» и «основание» не существуют).
Пример: номер 237 состоит из 3 цифр. Ясно, что одна цифра 7 больше цифры 2. Однако, как часть числа, двойка находится на месте сотен, а семерка — на месте единиц, так что количественное представление двойки остается двести или двести семь.
- шестидесятиричная (Древний Вавилон) — первая позиционная система счисления. До сих пор при измерении времени используется основание равное 60 (1 мин = 60 с, 1 ч = 60 мин);
- двенадцатеричная система счисления (широкое распространение получила в XIX в. Число12 — «дюжина»: в сутках две дюжины часов. Счет не по пальцам. а по суставам пальцев. На каждом пальце руки, кроме большого, по 3 сустава — всего 12;
Алфавит системы счисления — это набор различных цифр, используемых в позиционной системе счисления для записи чисел. Например: Десятичная система: Двоичная система: Октавная система: Шестнадцатеричная система:
- в позиционных системах счисления устранены все недостатки непозиционных:
- в них можно записать любое число (как натуральное, таки действительное);
- запись чисел компактна и удобна;
- благодаря поразрядной организации записи чисел с ними легко проводить математические операции.
Непозиционные системы счисления
Количество цифр в алфавите соответствует основанию системы счисления. Основание системы счисления — это количество цифр или знаков, используемых для представления числа в данной системе счисления.
Основой системы наименований является последовательность чисел, в которой каждая цифра имеет количественное значение или «вес». E.G: Основы некоторых систем ценности места. Десятичные: 10 0, 10 1, 10 2, 10 3, 10 4 ,…, 10 n ,…. Двоичные: 2 0, 2 1, 2 1, 2 2 2, 2 2 2, 2 2 2, 2 3, 2 4 ,…, 2 n ,…. Октава: 8 0, 8 1, 8 2, 8 3, 8 4 ,…, 8 n ,…. Пример. Десятичное число 4718.63, двоичное число 1001.1, восьмеричное число 7764.1, шестнадцатеричное число 3AF.
| I | V | X | L | С | D | М |
| 1 | 5 | 10 | 50 | 100 | 500 | 1000 |
Положение цифры в числе называется разрядной единицей: Цифры увеличиваются справа налево, от младшей к старшей цифре, начиная с нуля.
Русские не знали цифр, они заменяли их буквами с соответствующими значениями. Цифры обозначались специальным символом — титло — горизонтальной волнистой линией. Например, буква A соответствовала цифре 1, B — цифре 2, D — цифре 3. Десятки были представлены отдельными буквами: I — 10, К — 20, К — 30 и так далее, и сотни: С — 200, Х — 600.
- если большая цифра стоит перед меньшей, они складываются, например: VI – 6 (5+1);
- если меньшая цифра стоит перед большей, то из большей вычитается меньшая, причем в этом случае меньшая цифра уже повторяться не может, например: XL — 40 (50-10), XXL – нельзя;
- цифры М, С, Х, I могут повторяться в записи числа не более трех раз подряд;
- цифры D, L, V могут использоваться в записи числа только по одному разу.
Системы счисления
Начнем с определения системы счисления. Система счисления — это совокупность правил записи чисел цифровыми знаками.
Системы счисления бывают позиционные и непозиционные. В настоящее время и в технике и в быту широко используются как
позиционные, так и непозиционные системы счисления. Рассмотрим сначала примеры непозиционных систем счисления.
В качестве классического примера непозиционной системы счисления обычно приводят римскую форму записи чисел. Там не
менее это не единственная непозиционная система счисления, используемая в настоящее время.
Сейчас, как и в глубокой древности, для записи числа используются так называемые «палочки». Эта форма записи чисел
наиболее понятна и требует для записи числа всего один символ. Число образуется суммой этих «палочек». Однако при записи
больших чисел возникают неудобства. Число получается громоздким и его трудно читать.
В следующем варианте непозиционной системы счисления стали использовать несколько символов (цифр). Каждая цифра
обозначает различное количеств единиц. Конечное число точно так же как и в предыдущем варианте образуется суммой цифр.
Наиболее яркий вариант использования такой системы счисления — это денежные отношения. Мы с ними сталкиваемся
каждый день. Здесь никому не приходит в голову, что сумма, которую мы выкладываем за продукты, может зависеть от того, в
каком порядке мы расположим монеты на столе! Номинал монеты или банкноты не зависит от того, в каком порядке она была
вынута из кошелька. Это классический пример непозиционной системы счисления.
Однако чем большее число требуется представить в такой системе счисления, тем большее количество цифр требуется для
этого. Позиционные системы счисления были придуманы относительно недавно для того, чтобы сэкономить количество цифр,
используемое для записи чисел.
Значение цифры в позиционной системе счисления зависит от её позиции в записываемом числе. В позиционной системе
счисления появляются два очень важных понятия — основание системы счисления и вес цифры. Дело в том, что в
позиционной системе счисления число представляется в виде формулы разложения:
pnnn-1n-12211-1-1-2-2-k-k
где p — основание системы счисления
pi — вес единицы данного разряда
ai — цифры, разрешённые в данной системе счисления.
При этом количество цифр в системе счисления зависит от основания. Количество цифр равно основанию системы счисления.
В двоичной системе счисления две цифры, в десятичной — десять, а в шестнадцатеричной — шестнадцать.
Число в любой позиционной системе счисления записываются в виде последовательности цифр:
nn-121-1-2-k
где ai — цифры данной системы счисления, а цифра, соответствующая единицам определяется по
положению десятичной запятой (или десятичной точки в англоязычных странах). Каждая цифра, использованная в записи числа,
называется разрядом.
Какие же системы счисления применяются в настоящее время? Первый ответ, который я ожидаю — это десятичная
система счисления. А ещё? Да, да не удивляйтесь! Мы широко используем и другие системы счисления! Достаточно посмотреть
себе на левую руку. Там мы увидим часы. Сколько минут помещается в часе? Шестьдесят! Сколько секунд помещается в минуте?
Шестьдесят! Налицо признаки шестидесятеричной системы счисления. Это наследование древней вавилонской системы счисления,
которую вместе с компасом и часами европейцы заимствовали от арабов.
А еще примеры? Да сколько угодно! Картушка компаса делится на восемь румбов. Чем не восьмеричная система счисления?
А давно ли в России отказались от полушек (четверть копейки) или грошей (половина копейки)? А следующее значение
монеты — две копейки! Чем не двоичная система счисления?
Рассмотрим подробнее системы счисления, наиболее часто используемые в цифровой технике.
Перспективы развития
Преимущества троичной системы счисления перед двоичной
| Определение: |
| Троичная система счисления (англ. ternary numeral system) — позиционная система счисления с целочисленным основанием, равным . Существует в двух вариантах: несимметричная (, и др.) и симметричная (обычно или ). |
Троичная логика обладает рядом преимуществ перед двоичной. Ниже перечислены основные:
Троичная СС позволяет вмещать больший диапазон чисел в памяти троичного компьютера, поскольку 3^n\gt 2^n.
Очевидно, что троичная СС использует меньше разрядов для записи чисел, по-сравнению с двоичной СС. Например:
Для троичной СС используется несимметричный набор .
Эти два важных преимущества перед двоичной системой счисления говорят о большей экономичности троичной системы счисления.
| Определение: |
| Экономичность системы счисления (англ. radix economy) — возможность представления как можно большего количества чисел с использованием как можно меньшего общего количества знаков. |
Докажем экономичность троичной системы счисления математически.
Пусть – основание системы счисления, а – количество требуемых знаков. Для записи знаков потребуется разрядов, а количество чисел, которое при этом можно записать, будет равно .
Рассмотрим функцию .
Для того, чтобы определить максимальное значение функции, найдем ее производную:
, ближайшее число к — . Таким образом, троичная СС не только экономичнее двоичной, но и экономичнее любой другой СС.
Троичная логика включает в себя почти все возможности двоичной логики.
Компьютер, основанный на троичной логике, обладает большим быстродействием. Например, троичный сумматор и полусумматор в троичном компьютере при сложении тритов выполняет примерно в 1,5 раза меньше операций сложения по-сравнению с двоичным компьютером.
Проблемы реализации
Одним из барьеров, сдерживающих развитие и распространение троичной техники, является неверное представление о необычности и трудной постижимости трехзначной логики. Современная формальная логика (как традиционная, так и математическая) основана на принципе двузначности. Кроме того, электронные компоненты для построения логики, использующие более двух состояний, требуют больше материальных затрат на их производство, достаточно сложны в реализации, и потребляют больше электроэнергии, поэтому троичные компьютеры занимают очень малое место в истории.
Использование двоичных компьютеров — более простых и дешёвых в реализации — практически полностью затмило применение троичных компьютеров.
Практические реализации
Говоря о будущем таких машин, как «Сетунь» (то есть троичных компьютеров), известный американский учёный Дональд Кнут, отмечал, что они занимают очень мало место в отрасли вычислительной техники, что объясняется массовым засильем двоичных компонентов, производимых в огромных количествах. Но, поскольку троичная логика гораздо эффектнее, а главное, эффективнее двоичной, не исключено, что в недалёком будущем к ней вернутся.
В настоящий момент, в условиях интегральной технологии и микроэлектроники привлекательность троичной техники увеличивается: сложность трехзначных вентилей теперь не так страшна, а сокращение количества соединений и уменьшение рассеиваемой мощности особенно ценны. Особо благоприятное влияние на развитие троичное логики оказало пришествие квантовых компьютеров — вычислительных устройств, работающих на основе квантовой механики, принципиально отличающихся от классических компьютеров, работающих на основе классической механики.
Полноценный квантовый компьютер является пока гипотетическим устройством, сама возможность построения которого связана с серьёзным развитием квантовой теории в области многих частиц и сложных экспериментов; эта работа лежит на переднем крае современной физики.
Канадская компания D-Wave заявила в феврале 2007 года о создании образца квантового компьютера, состоящего из 16 кубит — квантовых аналогов битов.
Используя в универсальных квантовых вентилях кутриты вместо кубитов, можно существенно снизить количество необходимых вентилей.
Ланьон утверждает, что компьютер, который в обычном случае использовал бы 50 традиционных квантовых вентилей, сможет обойтись всего девятью, будучи основанным на троичном представлении.
Также, согласно некоторым исследованиям, использование кутритов вместо кубитов позволит упростить реализацию квантовых алгоритмов и компьютеров.
Таблицы истинности
При помощи тех же нулей и единиц создаются таблицы истинности логических выражений, в которых описаны всевозможные варианты.
Основные логические операции
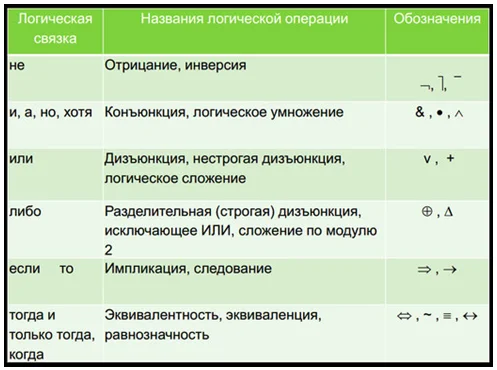
Например, конъюнкция является одной из логических операций. Она является истиной только в том случае, если два высказывания имеют истинные значения.
Логические переменные таблицы истинности обозначают p и q, а их значения выражают при помощи 0 и 1, где 0 – ложь, 1 – истина:
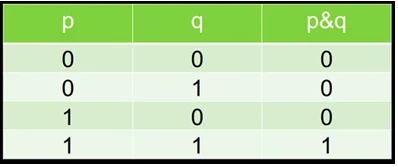
Фрагмент таблицы истинности для конъюнкции.
Так выражаются условия для всех логических операций.
Применяются таблицы истинности еще с начала 20 века в алгебре, логике, программировании.
Представление двоичных чисел
Чтобы обозначить, в какой системе счисления записано число, его снабжают указателем справа внизу. Например, запись числа 5 в десятичной форме обозначают как 510 и то же число в двоичной форме записи обозначают как 1012. В двоичной системе счисления (как и в других системах счисления, кроме десятичной) знаки читаются по одному. Например, число 1012 произносится «один ноль один».
Натуральные числа
В общем виде натуральное число, записываемое в двоичной системе счисления как (an−1an−2…a1a)2{\displaystyle (a_{n-1}a_{n-2}\dots a_{1}a_{0})_{2}}, выглядит следующим образом:
- (an−1an−2…a1a)2=∑k=n−1ak2k,{\displaystyle (a_{n-1}a_{n-2}\dots a_{1}a_{0})_{2}=\sum _{k=0}^{n-1}a_{k}2^{k},}
где:
- n{\displaystyle n} — количество цифр (знаков) в числе,
- ak{\displaystyle a_{k}} — значения цифр из множества {0,1},
- k{\displaystyle k} — порядковый номер позиции цифры (вес разряда).
Таким образом, по общему правилу представления числа в позиционной системе счисления, двоичное число в развёрнутом виде выглядит как сумма произведений числовых значений цифр из множества {0,1} на степень основания, то есть числа 2. Значение степени определяется порядковым номером позиции (разряда) справа налево, начиная с нулевой.
Например: 1012 = (1·22 + 0·21 + 1·2)10
Отрицательные числа
Отрицательные двоичные числа обозначаются так же как и десятичные: знаком «—» перед числом. А именно, отрицательное целое число в двоичной системе счисления (−an−1an−2…a1a)2{\displaystyle (-a_{n-1}a_{n-2}\dots a_{1}a_{0})_{2}} выглядит следующим образом:
- (−an−1an−2…a1a)2=−∑k=n−1ak2k.{\displaystyle (-a_{n-1}a_{n-2}\dots a_{1}a_{0})_{2}=-\sum _{k=0}^{n-1}a_{k}2^{k}.}
В вычислительной технике широко используется запись отрицательных двоичных чисел в дополнительном коде (обратный код числа, дополненный единицей в младшем разряде).
Дробные числа
Дробное число, записываемое в двоичной системе счисления как (an−1an−2…a1a,a−1a−2…a−(m−1)a−m)2{\displaystyle (a_{n-1}a_{n-2}\dots a_{1}a_{0},a_{-1}a_{-2}\dots a_{-(m-1)}a_{-m})_{2}}, имеет вид:
- (an−1an−2…a1a,a−1a−2…a−(m−1)a−m)2=∑k=−mn−1ak2k,{\displaystyle (a_{n-1}a_{n-2}\dots a_{1}a_{0},a_{-1}a_{-2}\dots a_{-(m-1)}a_{-m})_{2}=\sum _{k=-m}^{n-1}a_{k}2^{k},}
где:
- m{\displaystyle m} — количество цифр дробной части числа,
- ak{\displaystyle a_{k}} — значения цифр из множества {0,1}.
Веса цифр дробной части равны отрицательным степенями двойки, например:
- 101,1012 = (1·22 + 0·21 + 1·2 + 1·2–1 + 0·2–2 + 1·2–3)10 = 5,62510
При этом в виде конечных дробей в двоичной системе счисления можно записать только такие рациональные числа, где знаменатель является степенью двойки, другие же рациональные числа представляются в виде бесконечных двоичных дробей.
Почему троичная логика лучше двоичной
Троичная логика имеет несколько преимуществ перед двоичной:
- она позволяет более точно описывать некоторые процессы;
- в ней меньше ошибок, а эффективность работы устройства выше;
- её можно использовать для создания более мощных компьютеров и устройств.
Для понимания отличия двоичной логики от троичной сравним какие-то числа A и B. У этой задачи есть три варианта ответа: A > B, A = B и A < B. Двоичный процессор решит эту задачу за два прохода:
- сначала определит, равны ли числа A и B;
- если они не равны, то определит, больше ли A, чем B.
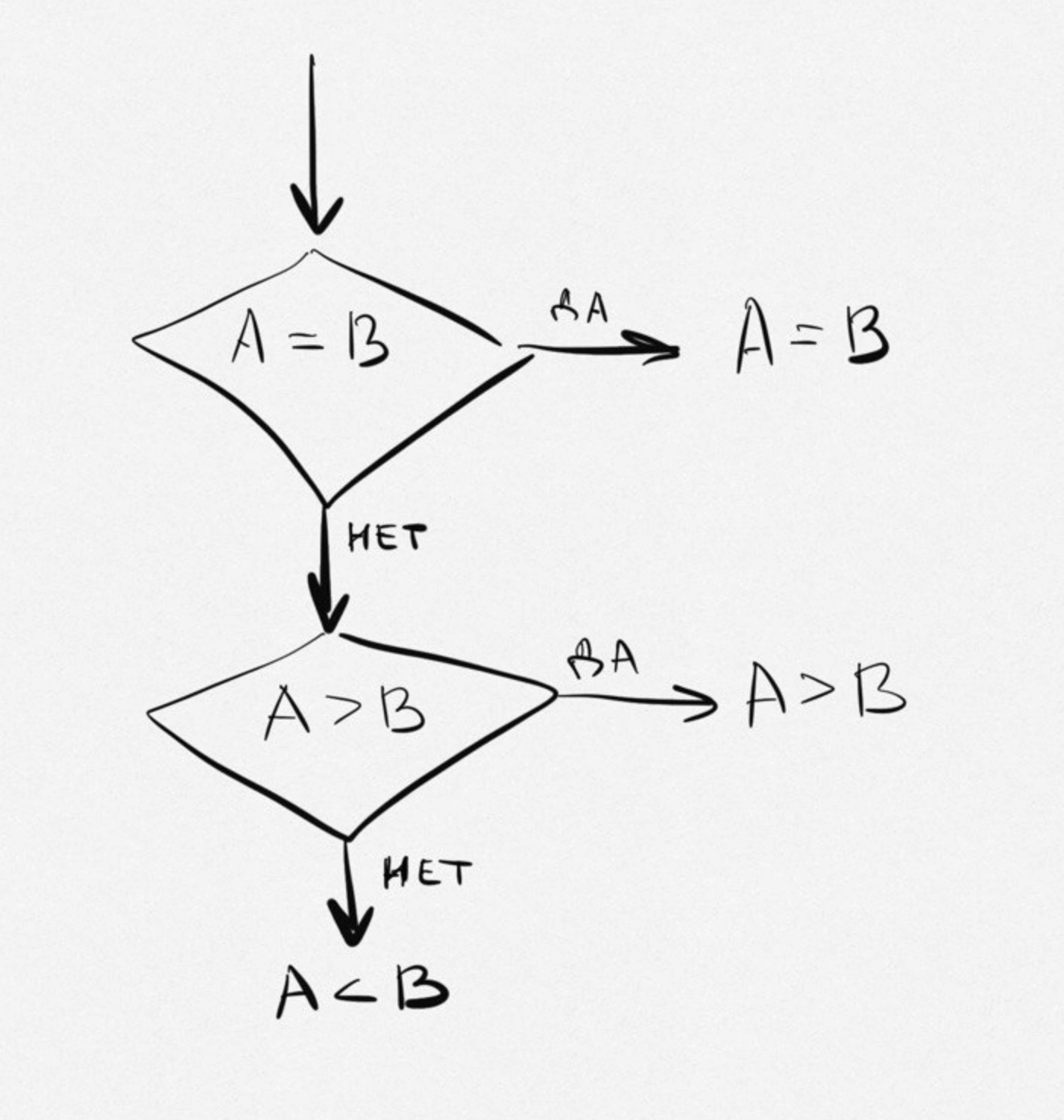
В троичной логике мы можем получить ответ сразу, за один проход.
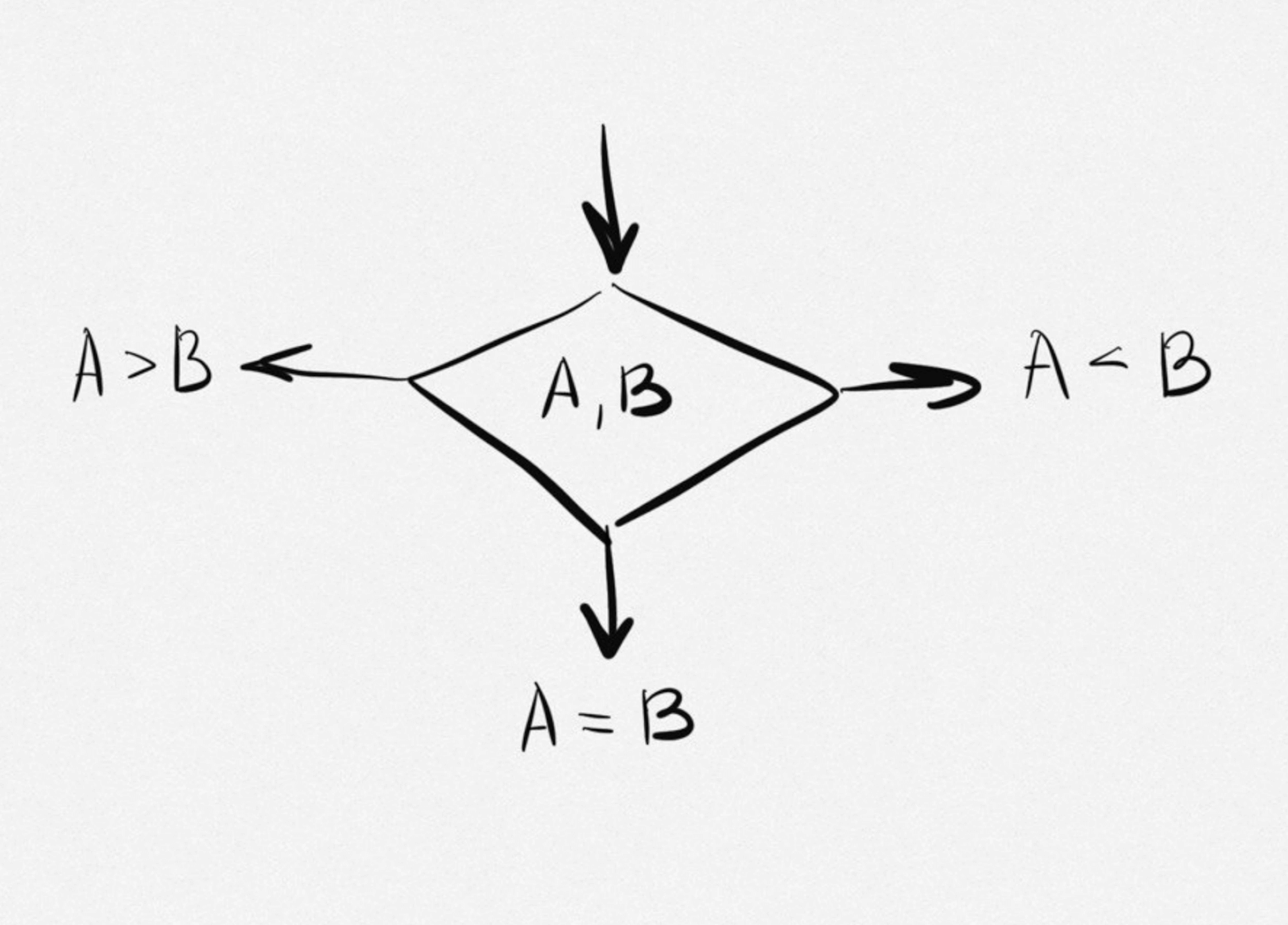
За счёт особенности хранения информации в тритах машины могут использовать меньше памяти для хранения:
| Биты | Триты |
| 16 | 10,09 |
| 32 | 20,19 |
| 64 | 40,38 |
| 128 | 80,76 |
Классификация позиционных систем
Двоичные
Определение
Двоичная система — система счисления, в которой в качестве базовых чисел выбираются степени числа два.
Чтобы не путать их с числами, записанными в десятичной системе счисления, справа внизу указывают основание системы счисления. Обычно число при этом заключают в скобки.
Двоичную систему использовали задолго до возникновения информационных технологий. Во втором тысячелетии до нашей эры народы Южной Америки кодировали двоичной системой свои записи, в том числе и не числовые. Узелок и ровный участок нити чередовались друг с другом.
В современной двоичной системе, на основе которой был создан телеграф, а позже — реле и переключатели, единица обозначает наличие сигнала, ноль — его отсутствие. Цифровые электронные схемы работают по тому же принципу. Также на нем основаны сигнальные системы, использующиеся до сих пор, например, азбука Морзе.
Восьмеричные
Когда-то два индейских племени решили, что им удобно при счете смотреть на восемь промежутков между пальцами, а не на сами пальцы. Восьмеричная система счисления отразилась в их языках, в которых только восемь слов, обозначающих цифры.
В двадцатом веке, когда для написания программ требовалось зашифровывать все больше информации в двоичной системе и упростить вычисления для людей, придумали альтернативную систему, которая позволила сократить количество цифр в коде. Число восемь — это два в кубе, поэтому перевести записи из двоичной системы в восьмеричную и обратно проще, чем в десятичную.
Десятичные
Элементы числовой базы, или ключевые числа, в десятичной системе счисления представляют собой степени десяти: 10 = 10^1, 100 = 10^2, 1000 = 10^3.
В системе всего десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Число 10 — основание системы счисления. Цифры от 0 до 9 представляют собой коэффициенты разложения числа по степеням десяти.
Родиной десятичной системы счисления считается Индия, хотя еще в вавилонской цивилизации с ее шестидесятеричной системой использовались закодированные десятичные цифры, а инки в своей узелковой письменности кодировали информацию десятью цветами. Но именно в Индии начали строго соблюдать порядок разрядов числа при записи и ставить ноль, чтобы избежать путаницы. Примерно в середине VIII века эту систему стали использовать другие страны. В Европе она распространилась к XVI веку и была названа «арабской».
Шестнадцатеричные
Шестнадцатеричные системы, как и восьмеричные, появились для упрощения взаимодействия с компьютером. Кроме арабских цифр, в них используются еще и латинские буквы от А до F. В разных языках программирования для записи чисел в шестнадцатеричной системе разные правила, называемые синтаксисом.
Пятеричная
Система, связанная с количеством пальцев на одной руке, использовалась в Китае и у некоторых племен Африки. В китайском языке у иероглифов, обозначающих цифры от шести до девяти, был один и тот же знак в начале — сокращенное обозначение цифры пять. Для записи чисел в этой системе используются цифры 0, 1, 2, 3, 4.
Двенадцатеричная
Если большим пальцем руки сосчитать число фаланг на других пальцах этой руки, получится двенадцать. Группы по двенадцать предметов называли во многих европейских языках словами, схожими с русским словом «дюжина»: duodezim на латыни, douzaine на французском, dozzina на итальянском, dozen на английском. Римляне пользовались двенадцатеричными дробями, \frac1{12} они называли унцией.
В Европе счет дюжинами долгое время, вплоть до XVIII века, сохранялся наравне с десятеричной системой. Дюжина дюжин составляла гросс (от немецкого слова «большой»), дюжина гроссов — массу. Признаки влияния числа 12 заметны в англо-американской системе линейных мер, в которой 1 фут равен 12 дюймам, 1 дюйм — 12 линиям, 1 линия — 6 точкам.
Шестидесятеричная
Первой позиционной системой счисления считается шестидесятеричная система в Древнем Вавилоне. Ее основание до сих пор применяют для измерения времени. Система счисления времени — смешанная, но для перевода минут в секунды или часы потребуется именно шестидесятеричная система.
Для измерения углов и записи координат (широты, долготы) тоже используют эту систему, так как изначально астрономические координаты записывали в шестидесятеричных дробях. По аналогии с часом градус делят на шестьдесят минут, минуту — на шестьдесят секунд.
Двадцатеричная
Двадцатеричную систему называют вигезимальной. Эта система, как и десятеричная, связана с количеством пальцев, поэтому многие народы изобрели ее независимо друг от друга. Основание 20 сохранилось в лингвистической структуре их языков, именно на нем основана система счета в разговорной речи. Например, во французском языке «восемьдесят» состоит из слов «четыре» и «двадцать».
Сравнение с другими базами
Для представления целого числа по основанию 3 требуется меньше цифр, чем для представления целого числа по основанию 2 . Например, десятичное число 220 записывается по основанию 2 11011100 (8 цифр), а по основанию 3 оно записывается как 22011 (5 цифр). Однако число, записанное по основанию 3, длиннее, чем по основанию 10; по этой причине в информатике троичные числа иногда кодируются по основанию 9 или 27 , точно так же, как двоичные числа уплотняются по основанию 8 или .
| Тернарный | 1 | 2 | 10 | 11 | 12 | 20 | 21 | 22 | 100 |
|---|---|---|---|---|---|---|---|---|---|
| Треки | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 |
| Десятичный | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Тернарный | 101 | 102 | 110 | 111 | 112 | 120 | 121 | 122 | 200 |
| Треки | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 | 10000 | 10001 | 10010 |
| Десятичный | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Тернарный | 201 | 202 | 210 | 211 | 212 | 220 | 221 | 222 | 1000 |
| Треки | 10011 | 10100 | 10101 | 10110 | 10111 | 11000 | 11001 | 11010 | 11011 |
| Десятичный | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| Тернарный | 1 | 10 | 100 | 1 000 | 10 000 |
|---|---|---|---|---|---|
| Треки | 1 | 11 | 1001 | 1 1011 | 101 0001 |
| Десятичный | 1 | 3 | 9 | 27 | 81 |
| Сила | 3 | 3 1 | 3 2 | 3 3 | 3 4 |
| Тернарный | 100 000 | 1 000 000 | 10 000 000 | 100 000 000 | 1 000 000 000 |
| Треки | 1111 0011 | 10 1101 1001 | 1000 1000 1011 | 1 1001 1010 0001 | 100 1100 1110 0011 |
| Десятичный | 243 | 729 | 2 187 | 6 561 | 19 683 |
| Сила | 3 5 | 3 6 | 3 7 | 3 8 | 3 9 |
Что касается рациональных чисел , то троичная система удобна для представления дробей, имеющих степень 3 в качестве знаменателя, которые в десятичной системе счисления представлены периодическими числами . Однако, поскольку в основе нет простых множителей, отличных от 3, все остальные нецелочисленные рациональные числа становятся периодическими. Например, вот некоторые дроби с соответствующими основаниями 2, 3 и 10:
| Тернарный | 0. 1 11111111111 … | 0,1 | 0. 02 0202020202 … | 0. 0121 01210121 … | 0,0 1 1111111111 … | 0. 010212 010212 … |
|---|---|---|---|---|---|---|
| Треки | 0,1 | 0,01 0101010101 … | 0,01 | 0. 0011 00110011 … | 0,0 01 01010101 … | 0. 001 001001001 … |
| Десятичный | 0,5 | 0. 3 33333333333 … | 0,25 | 0,2 | 0,1 6 6666666666 … | 0. 142857 142857 … |
| Дробная часть | 1/2 | 1/3 | 1/4 | 1/5 | 1/6 | 1/7 |
| Тернарный | 0,01 0101010101 … | 0,01 | 0. 0022 00220022 … | 0. 00211 0021100 … | 0.0 02 020202020 … | 0. 002 002002002 … |
| Треки | 0,001 | 0. 000111 000111 … | 0,0 0011 0011001 … | 0. 0001011101 00 … | 0,00 01 01010101 … | 0. 000100111011 … |
| Десятичный | 0,125 | 0. 1 11111111111 … | 0,1 | 0. 09 0909090909 … | 0,08 3 333333333 … | 0. 076923 076923 … |
| Дробная часть | 1/8 | 1/9 | 1/10 | 1/11 | 1/12 | 1/13 |
Шестнадцатеричная СС
Умножение до 8 СС
Как только люди научились считать, возникла необходимость в изобретении чисел.
Для простоты люди стали группировать палочки по 3, 5 или 10 штук. У каждой группы был определенный знак или предмет. Первоначально для нумерации использовались пальцы, так появились первые обозначения для групп из 5 и 10 (единиц). Это позволило создать более удобные системы записи чисел.
Алгоритм преобразования чисел в 16СС
Древнеегипетская десятичная система
В Древнем Египте для обозначения чисел 1, 10, 10 2, 10 3, 10 4, 10 5, 10 6, 10 7 использовались специальные символы (нумералы). Вот некоторые из них:




























