Наибольшее возможное целочисленное решение | Wyzant Спросите эксперта
Алгебра 1
Саванна Дж.
Каково максимально возможное целочисленное решение неравенства 3,829x
Подписаться
І
1
Подробнее
Отчет
2 ответа от опытных наставников
Мэтью С.![]()
Репетитор
5
(123)
Аспирант по химии Вашингтонского университета
См. таких репетиторов
Смотрите таких репетиторов
3,829x
x
x
Таким образом, максимальное целочисленное значение x, которое может принимать значение:
x = 7
Голосовать за 0 голос против
Подробнее
Отчет
Натан С.
ответил 21.06.19
Репетитор
Новое в Византе
Терпеливый и знающий преподаватель, специализирующийся на математике и естественных науках
Смотрите таких репетиторов
Смотрите таких репетиторов
Целое число определяется как целое число, по сути, число, не являющееся дробью.
Чтобы найти максимально возможное целочисленное решение 3,829x
Давайте решим 3,829x = 28,195
x = 28,195/3,829
x = 7,3635
7,3635 не является целым числом, но давайте подставим два соседних целых числа обратно в исходную задачу и посмотрим, какое из них работает. Два ближайших целых числа к 7,3635 — это 7 (внизу) и 8 (вверху).
Попробуем x = 8
3,829(x)
3,829(8)
30,632
ЛОЖЬ… x не может равняться 8, так как 30,632 не меньше 28,195
Попробуем x = 7
3,829(x)
3,829(7)
26,803
ИСТИНА… x может равняться 7, поскольку 26,803 меньше 28,195
Следовательно, максимально возможное целочисленное решение равно x = 7
Надеюсь, это полезно!
Голосовать за 0 голос против
Подробнее
Отчет
Получите бесплатный ответ на быстрый вопрос. Ответы на большинство вопросов в течение 4 часов.
ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и встретьтесь онлайн.
Никаких пакетов или подписок, платите только за то время, которое вам нужно.
Числовые неравенства
Вы умеете сравнивать целые числа, десятичные дроби. Знаете правила сравнения обыкновенных дробей с одинаковыми знаменателями, но разными числителями; с одинаковыми числителями, но разными знаменателями. Здесь вы научитесь сравнивать любые два числа с помощью нахождения знака их разности.
Сравнение чисел широко применяется на практике. Например, экономист сравнивает плановые показатели с фактическими, врач сравнивает температуру больного с нормальной, токарь сравнивает размеры вытачиваемой детали с эталоном. Во всех таких случаях сравниваются некоторые числа. В результате сравнения чисел возникают числовые неравенства.
Определение. Число а больше числа b, если разность а-b положительна. Число а меньше числа b, если разность а-b отрицательна.
Если а больше b, то пишут: а > b; если а меньше b, то пишут: а b означает, что разность а – b положительна, т.е. а – b > 0. Неравенство а b, a = b, a , = или b и b > с, то а > с.
Теорема. Если к обеим частям неравенства прибавить одно и то же число, то знак неравенства не изменится. Следствие. Любое слагаемое можно перенести из одной части неравенства в другую, изменив знак этого слагаемого на противоположный.
Теорема. Если обе части неравенства умножить на одно и то же положительное число, то знак неравенства не изменится. Если обе части неравенства умножить на одно и то же отрицательное число, то знак неравенства изменится на противоположный. Следствие. Если обе части неравенства разделить на одно и то же положительное число, то знак неравенства не изменится. Если обе части неравенства разделить на одно и то же отрицательное число, то знак неравенства изменится на противоположный.
Вы знаете, что числовые равенства можно почленно складывать и умножать. Далее вы научитесь выполнять аналогичные действия с неравенствами. Умения почленно складывать и умножать неравенства часто применяются на практике. Эти действия помогают решать задачи оценивания и сравнения значений выражений.
При решении различных задач часто приходится складывать или умножать почленно левые и правые части неравенств. При этом иногда говорят, что неравенства складываются или умножаются. Например, если турист прошёл в первый день более 20 км, а во второй – более 25 км, то можно утверждать, что за два дня он прошёл более 45 км. Точно так же если длина прямоугольника меньше 13 см, а ширина меньше 5 см, то можно утверждать, что площадь этого прямоугольника меньше 65 см2.
При рассмотрении этих примеров применялись следующие теоремы о сложении и умножении неравенств:
Теорема. При сложении неравенств одинакового знака получается неравенство того же знака: если а > b и c > d, то a + c > b + d.
Теорема. При умножении неравенств одинакового знака, у которых левые и правые части положительны, получается неравенство того же знака: если а > b, c > d и а, b, с, d – положительные числа, то ac > bd.
Неравенства со знаком > (больше) и 1/2, 3/4 b, c и и b, quad ax
Понятие равенства
Под этим термином понимают высказывания, в записи которых есть знак «=». Равенства разделяются на верные и неверные. Если в записи вместо = стоит , тогда речь идет о неравенствах. Кстати, первый признак равенства говорит о том, что обе части выражения идентичны по своему результату или записи.

Кроме понятия равенства, в школе изучают также тему «Числовое равенство». Под этим высказыванием понимают два числовых выражения, которые стоят по обе стороны от знака =. К примеру, 2*5+7=17. Обе части записи равны между собой.
В числовых выражениях подобного типа могут использоваться скобки, влияющие на порядок действий. Итак, существует 4 правила, которые следует учесть при вычислении результатов числовых выражений.
- Если в записи нет скобок, тогда действия выполняются с высшей ступени: III→II→I. Если есть несколько действий одной категории, тогда они выполняются слева направо.
- Если в записи есть скобки, тогда действие выполняется в скобках, а затем с учетом ступеней. Возможно, в скобках будет несколько действий.
- Если выражение представлено в виде дроби, тогда вычислять нужно сначала числитель, потом знаменатель, затем числитель делится на знаменатель.
- Если в записи есть вложенные скобки, тогда вычисляется сначала выражение во внутренних скобках.
Итак, теперь понятно, что такое равенство. В дальнейшем будут рассмотрены понятия уравнения, тождества и способы их вычисления.
Дробно-рациональные неравенства
До сих пор мы рассматривали целые нер-ва. Однако, по аналогии с уравнениями, существуют ещё и дробно-рациональные нер-ва. В них выражение с переменной может стоять в знаменателе. Приведем примеры дробно-рациональных нер-в:
Любое такое нер-во можно представить в виде
где Р(х) и Q(х) – некоторые многочлены. Естественно, вместо знака «>» может стоять и другой знак. Для примера преобразуем к такому виду нер-во
Перенесем все слагаемые влево:
Далее приведем левую часть к общему знаменателю:
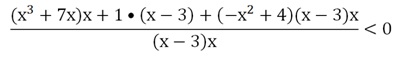
Осталось раскрыть скобки:
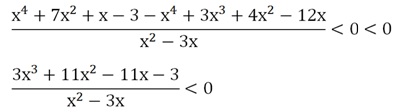
В итоге и в числителе, и в знаменателе стоят многочлены.
Рассмотрим нер-ва
а/b>0 и ab> 0
Докажем, что они равносильны друг другу. Возможны 5 случаев:
- И а, и b являются положительными числами. Тогда оба нер-ва верны, ведь и произведение, и отношение двух положительных чисел само положительно:
10•5 = 50 > 0
10/5 = 2 > 0
- Оба числа, а и b, отрицательны, тогда снова оба нер-ва справедливы, ведь при умножении и делении двух отрицательных чисел получается положительное число. Например:
(– 10)•(– 5) = 50 > 0
(– 10)/(– 5) = 2 > 0
- Только одно из чисел положительно, а другое отрицательно, тогда их произведение, как и частное, меньше нуля, и нер-ва неверны:
(– 10)•5 = – 50< 0
(– 10):5 = – 2 < 0
- Число a равно нулю. Тогда выражения ab и a/b также равны нулю, а потому рассматриваемые нер-ва неверны:
0•5 = 0
0/5 = 0
- Число b равно нулю. Тогда произведение ab равно нулю, а дробь а/b не имеет смысла (из-за нуля в знаменателе). То есть нер-ва а/b> 0 и ab> 0 снова одновременно неверны.
Получили, что при любых значениях а и b нер-ва а/b> 0 и ab> 0 либо одновременно справедливы, либо одновременно несправедливы. Это значит, что они равносильны.

Это значит, что от дробно-рационального нер-ва можно перейти к равносильному ему целому нер-ву.
Пример. Решите нер-во
Решение:
Исходному нер-ву равносильно иное нер-во:
(х – 1)(х – 2)(х – 3)(х – 4)> 0
Решим его методом интервалов:
Получаем, что х∊(1; 2)∪(3; 4).
Ответ: (1; 2)∪(3; 4).
Пример. Решите нер-во
Решение. В числителе и знаменателе находятся квадратные трехчлены. Их можно разложить на корни, если знать их корни. Найдем их.
х2 – 9х + 14 = 0
D = b2– 4ас = (– 9)2 – 4•1•14 = 84 – 56 = 25
х1 = (9 – 5)/2 = 2
х2 = (9 + 5)/2 = 7
Так как корни равны 2 и 7, то можно записать, что
х2 – 9х + 14 = (х – 2)(х – 7)
Аналогично разложим знаменатель
х2 – 14х + 45 = 0
D = b2– 4ас = (– 14)2 – 4•1•45 = 196 – 180 = 16
х1 = (14 – 4)/2 = 5
х2 = (14 + 4)/2 = 9
х2 – 14х + 45 = (х – 5)(х – 9)
Перепишем исходное нер-во:
Ему равносильно другое нер-во:
(х – 2)(х – 7)(х – 5)(х – 9) > 0
Его можно решить методом интервалов:
Получаем, что х∊(– ∞; 2)∪(5; 7)∪(9; + ∞).
Ответ: х∊(– ∞; 2)∪(5; 7)∪(9; + ∞).
Обратим внимание на одну особенность метода интервала в случаях, когда решается дробно-рациональное нер-во. Она касается нестрогих нер-в (со знаками «≤» и «≥»)
В целых нестрогих нер-вах сами точки, при которых выражение слева обращается в ноль, включаются в решение
Но при рассмотрении дроби важно понимать, что ее знаменатель не может быть равным нулю. Поэтому при нестрогом нер-ве в ответ надо включить точки, обращающие в ноль числитель, но при этом исключить точки, обращающие в ноль знаменатель
Пример. Решите нер-во
Числитель обращается в ноль в точках (– 2) и 4, а знаменатель – в точках (– 7) и 8. Так как нер-во нестрогое, то числа 4 и (– 2) будут входить в решение (на координатной прямой мы отметим их закрашенным кружочком), а числа (– 7) и 8 – нет (их отметим как «выколотые точки»):
В итоге получаем, что дробь неотрицательна при х∊(– ∞; – 7)∪∪(8; – ∞).
Ответ: (– ∞; – 7)∪∪(8; – ∞).
Применение линейного неравенства в реальной жизни
Линейное неравенство вездесущему в современном мире, и они используются в различных областях для моделирования реальных ситуаций.Одним из примеров является экономика, где линейное неравенство используется для представления ограничений на доступные ресурсы.Например, компания, производящая товары, имеет ограниченный бюджет на рекламу и производство, и компания должна убедиться, что она остается в рамках бюджета.Ограничения на бюджет могут быть смоделированы с использованием линейного неравенства, и компания может использовать алгебраические методы для поиска оптимального решения.Точно так же линейное неравенство используется в транспортировке и логистике для представления ограничений на перемещение товаров и людей.
1. В финансах линейное неравенство используется для представления ограничений на инвестиции.Например, менеджер портфеля, возможно, должен обеспечить, чтобы портфель оставался в пределах определенного уровня риска, а ограничения на риск могут быть смоделированы с использованием линейного неравенства.Менеджер может затем использовать алгебраические методы, чтобы найти наилучший баланс между риском и доходностью.
2. В инженерии и физике линейное неравенство используется для представления ограничений на физический мир.Например, максимальная нагрузка, которую может переносить мост, может быть представлена с использованием линейного неравенства, и инженеры могут использовать алгебраические методы для соответствующего проектирования моста.Точно так же максимальная скорость, которую автомобиль может проходить вокруг кривой, может быть представлена с использованием линейного неравенства, и физики могут использовать алгебраические методы для изучения движения автомобиля.
3. В науке о окружающей среде линейное неравенство используется для представления ограничений на использование ресурсов.Например, максимальное количество загрязнения, которое может переносить реку, может быть представлено с использованием линейного неравенства, и ученые -экологи могут использовать алгебраические методы, чтобы найти лучшую политику для уменьшения загрязнения.
4. В социальных науках линейное неравенство используется для представления ограничений на поведение человека.Например, максимальное количество времени, которое человек может потратить на социальные сети, может быть представлено с использованием линейного неравенства, и психологи могут использовать алгебраические методы для изучения влияния социальных сетей на поведение человека.
Таким образом, линейные неравенства используются в различных областях для моделирования реальных ситуаций.Они являются важными инструментами для принятия решений, а алгебраические методы обеспечивают систематический подход к поиску оптимальных решений.
Применение линейного неравенства в реальной жизни — Линейное неравенство: борьба с линейными неравенствами с помощью алгебраических методов
Роль наибольшего целого решения в различных областях
Наибольшее целое решение неравенств играет важную роль в различных областях, где требуется найти определенные значения или ограничения. Это понятие может быть полезно в математике, программировании, экономике и других науках. Ниже приведены некоторые области, в которых наибольшее целое решение имеет особое значение:
-
Математика: Наибольшее целое решение используется для округления чисел. Например, если нужно найти наибольшее целое число, меньшее или равное заданному числу, применяется наибольшее целое решение. Это позволяет получить целое число для дальнейших вычислений или анализа данных.
-
Программирование: В программировании наибольшее целое решение используется для ограничения значений или индексов. Например, если требуется обрабатывать только целочисленные значения или индексы, наибольшее целое решение помогает обеспечить корректную работу программы.
-
Экономика: В экономике наибольшее целое решение может использоваться для округления денежных сумм или количества товаров. Например, при расчете налогов или цен на товары, может потребоваться использование наибольшего целого решения для получения точных значений.
-
Физика: Наибольшее целое решение может применяться в физике для учета дискретности или квантования величин. Например, при анализе энергетических уровней или атомных состояний может использоваться наибольшее целое решение для представления ограниченных значений энергии или момента импульса.
Во всех этих областях наибольшее целое решение помогает получить целочисленные значения или ограничения, которые удовлетворяют требуемым условиям. Это приносит пользу при решении практических задач и облегчает математические выкладки.
Почему неравенства не решают так же, как уравнения?
Пример 1
Решить уравнение:
Итак, нужно найти корни уравнения. Что можно сделать?
Вариант первый.
Зафиксировать область допустимых значений (ОДЗ) выражения: \( x-1 \ne 0; \; x+5 \ne 0. \)
Убедиться в том, что уравнение представляет собой равенство двух дробей и воспользоваться основным свойтвом пропорции — произведение крайних членов пропорции равно произведению её средних членов — в просторечии «перемножить крест накрест.»
\
Решить простое (без дробей) рациональное уравнение. Здесь после раскрытия скобок и приведения подобных членов оно сведется к квадратному.
Сверить полученные корни с ОДЗ и, отбросив лишние, сформировать ответ.
Вариант второй.
Привести к общему знаменателю
При этом неважно перенесены ли предварительно все члены уравнения в одну сторону или нет. Не забыть об ограниченности области допустимых значений выражения (написать ОДЗ).Отбросить общий знаменатель (одинаковые знаменатели в обеих частях равенства, если не переносили всё в одну сторону). Решить упрощенное уравнение, проверить полученные корни на соответствие ОДЗ, написать ответ
Решить упрощенное уравнение, проверить полученные корни на соответствие ОДЗ, написать ответ.
Вариант третий.
Перенести все члены уравнения в левую часть равенства и привести к общему знаменателю.
\
Затем, вспомнив о том, что дробь равна нулю, когда её числитель равен нулю, а знаменатель не равен нулю, записать и решать следующую равносильную систему:
\
Попробуйте всё это проделать самостоятельно для тренировки навыков решения дробно-рациональных уравнений. И убедитесь в том, что во всех трёх случаях будут получены одинаковые ответы.Для решения уравнений реального ЕГЭ вы можете выбрать любой из этих подходов, который вам придётся по душе.
Ответ:
Замечение:Отдельные ответы удобно записывать в фигурных скобках как элементы перечислимого множества, в отличие от интервалов (a;b) и отрезков , для обозначения которых используются круглые или квадратные скобки соответственно..
Пример 2
Решить неравенство:
Это неравенство содержит те же самые дробные выражения, что и предыдущее уравнение. Однако теперьварианты «крест накрест» и отбрасывание общего знаменателя НЕПРИМЕНИМЫ, потому что в знаменателе присутствуют неизвестные величины, а следовательно мы не знаем знаков множителей и не сможем корректно применять свойства неравенств. Особенно это касается свойства 5, которое требует изменить знак неравенства при умножении на отрицательное число. Поэтому при решении дробно-рационального неравенствасамое разумное действие — перенести все его члены в одну сторону и сравнивать итоговое выражение с нулем, т.е. применим способ аналогичный рассмотренному варианту 3 для уравнений.
Далее можем рассуждать так:
Фактически, здесь мы должны определить знак дробного выражения. То есть при каких значениях переменной результат деления является неположительным числом (отрицательным или нулём).
Очевидно, это будет тогда, когда знаки числителя и знаменателя не совпадают. Таким образом, нужно рассмотреть два случая: числитель дроби меньше либо равен нулю И знаменатель положителен (> 0) ИЛИ числитель дроби больше либо равен нулю И знаменатель отрицателен (
Это рассуждение приводит нас к совокупности двух систем неравенств
Обратите внимание, если в текст размышлений можно вставить союз «И», то это система, в которой выражения мы соединяем обычно фигурной скобкой «{«, если же можно вставить союз «ИЛИ», т.е. объединить несколько разных случаев, то это совокупность, обозначаемая квадратной скобкой «»
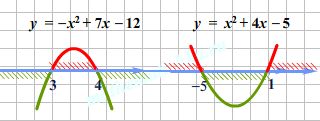
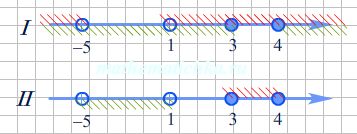
Ответ: .
Сравним ответ неравенства с ответом уравнения, рассмотренного выше. Значения переменной \(x = -5; x = 1; x = 3; x = 4 \) присутствовали как ключевые при решении уравнения, однако те из них, которые обращают знаменатель в 0, не вошли в ответ.
Но в ответе неравенства мы явно видим все эти значения переменной. Они фигурируют как границы промежутков. При этом входят или не входят граничные точки в ответ зависит от ОДЗ выражений и степени строгости неравенства.
Таким образом, наиболее частые ошибки при решении неравенств состоят в потере граничных точек и слиянии промежутков.
Определение количества целочисленных решений неравенств: основные принципы и методы
Определение количества целочисленных решений неравенств является важной задачей в алгебре и математическом анализе. Эта задача заключается в нахождении всех целых чисел, которые удовлетворяют некоторому неравенству. Количество таких целочисленных решений может быть разным в зависимости от вида неравенства и конкретных ограничений
Количество таких целочисленных решений может быть разным в зависимости от вида неравенства и конкретных ограничений.
Существует несколько основных принципов и методов, которые позволяют определить количество целочисленных решений неравенств:
- Метод перебора: этот метод заключается в переборе всех возможных значений целых чисел в заданном диапазоне и проверке их удовлетворения неравенству. Хотя этот метод может быть эффективен для небольших значений, он становится неэффективным при больших ограничениях или сложных неравенствах.
- Использование математических свойств и теорем: в некоторых случаях можно использовать известные математические свойства и теоремы для определения количества целочисленных решений. Например, если неравенство является линейным или квадратичным, можно использовать методы алгебры для нахождения всех решений.
- Анализ графика функции: графический метод позволяет визуализировать неравенство и определить область, в которой находятся целочисленные решения. Для этого строится график функции, соответствующей неравенству, и анализируется его поведение на целых числах.
- Использование теории делимости: теория делимости позволяет выполнять различные операции с числами и применять различные алгоритмы для определения наличия целочисленных решений неравенств. Например, можно использовать разложение чисел на простые множители или алгоритм Евклида для нахождения наибольшего общего делителя.
Количество целочисленных решений неравенств может быть разным и зависит от типа неравенства, ограничений и специфических условий
Важно правильно выбрать метод и применить соответствующие математические инструменты для решения данной задачи
В заключение, определение количества целочисленных решений неравенств является сложной задачей, требующей применения различных принципов и методов. Правильный выбор метода и использование математического аппарата позволяют найти все целочисленные решения и получить точный ответ на поставленную задачу.
Метод интервалов
Методом интервалов решают неравенства, приведенные к виду F(x)>0 или F(x)
Метод интервалов основан на том, что непрерывная на промежутке функция может менять знак только в тех точках, где ее значения равно нулю (но может и не менять).
Алгоритм метода интервалов:
- Найти область определения функции D(F(x)) и промежутки, на которых F(x)непрерывна.
- Найти нули функции F(x) – значения x, при которых F(x) = 0.
- Нанести на числовую ось найденные промежутки и нули.
- Определить интервалы знакопостоянства и в каждом из них поставить найденный подсчетом знак.
- Написать ответ.
Рассмотрим пример применения данного метода для решения неравенства \(\frac{(x-1)^2 (x-2)^3}{x} > 0\):
1. Функция \(\frac{(x-1)^2 (x-2)^3}{x}\) непрерывна в каждой точке своей области определения (это дробно–рациональная функция).
2. Найдем точки, в которых наша функция F(x)=0, т.е. в данном случае задача сводится к решению соответствующих уравнений: (x-1)=0 или (x-2)=0 или x=0. В результате получили точки x=1, x=2 и x=0.
3. Нанесем на числовую ось найденные промежутки и нули:
4. Найдем знак правого промежутка. Берем любое число, которое больше, чем x=1. Например, x=10. Тогда получим:
$$ f(x)=x(x-1)^2 (x-2)^3 \\ f(10)=10(10-1)^2 (10-2)^3 = 298 > 0 $$
Расставляем остальные знаки. В точке x=1, уравнение (x-1)^2- четное, следовательно, знак остается без изменений; в точке x=2, (x-2)^3 — нечетное, знак функции изменяется на противоположный.
5. Вернемся к исходному неравенству: F(x)>0, следовательно, нам необходимо записать в ответ интервалы отмеченные знаком плюс.
Ответ: \(x \in (-\infty;0)\cup(2;+\infty)\).
Методы и советы по поиску наибольшего целого решения
Поиск наибольшего целого решения неравенства может быть сложной задачей, особенно если уравнение содержит переменные и нелинейные функции. Однако с использованием определенных методов и советов можно упростить этот процесс. В этом разделе мы рассмотрим несколько таких подходов, которые могут помочь вам найти наибольшее целое решение вашего неравенства.
1. Используйте метод подстановки. В некоторых случаях можно выбрать некоторые значения переменных и подставить их в исходное неравенство, чтобы определить, какие значения удовлетворяют условию. Например, если вам нужно найти наибольшее целое решение для неравенства 2x + 3 < 10, вы можете начать с подстановки различных значений x, начиная с наибольшего целого числа, пока неравенство не будет выполняться.
2. Примените алгоритм полного перебора. Если у вас есть ограниченное множество значений переменных, вы можете использовать алгоритм полного перебора, перебирая все возможные комбинации значений и проверяя, какие из них удовлетворяют условию неравенства. Этот метод может быть неэффективным для больших множеств значений, но может быть полезным в некоторых случаях.
3. Используйте математические свойства. Некоторые неравенства могут быть упрощены с использованием известных свойств математических операций и функций. Например, если у вас есть неравенство вида x^2 > 16, вы можете применить функцию корня к обеим сторонам уравнения и найти все значения x, которые удовлетворяют новому условию.
4. Используйте таблицу значений. Построение таблицы значений может помочь визуализировать, какие значения переменных удовлетворяют условию неравенства. Вы можете начать с наибольшего целого числа, постепенно уменьшая его и проверяя, выполняется ли неравенство для каждого значения.
Важно помнить, что поиск наибольшего целого решения неравенства может требовать некоторого времени и усилий. Избегайте опечаток при проведении вычислений и не забывайте проверять полученные результаты
В случае необходимости, обратитесь за помощью к математическому программному обеспечению или онлайн-калькуляторам, чтобы упростить процесс поиска наибольшего целого решения вашего неравенства.
| Метод | Описание |
|---|---|
| Метод подстановки | Выбор некоторых значений переменных и подстановка их в неравенство для определения удовлетворяющих условию значений. |
| Алгоритм полного перебора | Перебор всех возможных комбинаций значений переменных и проверка, какие из них удовлетворяют условию неравенства. |
| Использование математических свойств | Упрощение неравенства с использованием известных свойств математических операций и функций. |
| Использование таблицы значений | Построение таблицы значений для визуализации, какие значения переменных удовлетворяют условию неравенства. |
Неравенства высоких степеней
Напомним, что если некоторое число а – корень многочлена Р(х) (то есть оно является корнем ур-ния Р(х) = 0), то этот многочлен можно представить как произведение двучлена (х – а) и какого-то другого многочлена Р1(х). Другими словами, зная корни многочлена, можно разложить его на множители. За счет этого можно решать нер-ва высоких степеней.
Пример. Решите нер-во
х3 – 3х2 – х + 3 < 0
Решение. Найдем корни многочлена, стоящего в левой части, то есть решим ур-ние
х3 – 3х2 – х + 3 = 0
Попробуем подобрать корни, начав с целых чисел. Напомним, что все целые корни должны быть делителем свободного члена, то есть в данном случае числа 3. Поэтому «кандидатами» являются числа 1, (– 1), 3 и (– 3). Подставляя их в ур-ние, находим, что оно имеет три корня: 1, (– 1) и 3:
13 – 3•12 – 1 + 3 = 1 – 3 – 1 + 3 = 0
(– 1)3 – 3•(– 1)2 – (– 1) + 3 = – 1 – 3 + 1 + 3 = 0
33 – 3•32 – 3 + 3 = 27 – 27 – 3 + 3 = 0
Число (– 3) не подходит, ведь при его подстановке в левую часть ноль не получается:
(– 3)3 – 3•(– 3)2 – (– 3) + (– 3) = – 27 +27 + 3 + 3 = 6
Напомним, что у ур-ния 3-ей степени не может быть более 3 корней, поэтому других корней у ур-ния нет.
Зная корни, мы можем разложить многочлен на множители:
х3 – 3х2 – х + 3 = (х – 1)(х + 1)(х – 3).
В справедливости такого разложения можно убедиться, раскрыв скобки в правой части этого равенства. Теперь можно переписать исходное нер-во
х3 – 3х2 – х + 3 < 0
(х – 1)(х + 1)(х – 3) < 0
Найдем его решение методом интервалов:
Убедимся в том, что мы правильно расставили знаки, подставляя в нер-во произвольные числа из промежутков:
при х = – 2 имеем (– 2 – 1)(– 2 + 1)(– 2 – 3) = (– 3)•(– 1)•(– 5) < 0
при х = 0 получится (0 – 1)(0 + 1)(0 – 3) = (– 1)•1•(– 3) > 0
при х = 2 имеем (2 – 1)(2 + 1)(2 – 3) = 1•3•(– 1) < 0
при х = 4 получится (4 – 1)(4 + 1)(4 – 3) = 3•5•1 > 0
Получаем, что левая часть отрицательна при х∊(– ∞; – 1)∪(1; 3).
Ответ:(– ∞; – 1)∪(1; 3).
Пример. Решите нер-во
х3 + 2х – 3 > 0
Решение. Рассмотрим ур-ние
х3 + 2х – 3 = 0
Подбором можно определить лишь один его корень – единицу:
13 + 2•1 – 3 = 0
Поделим исходный многочлен на (х – 1):
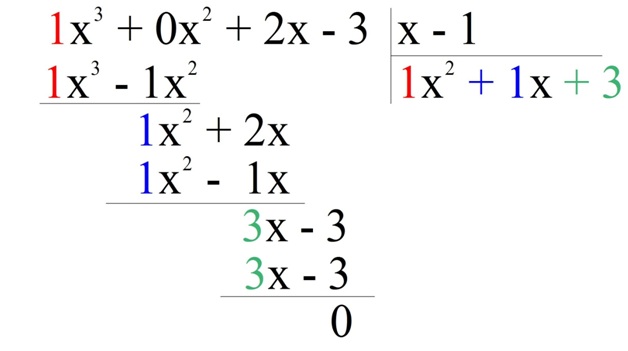
Получили, что х3 + 2х – 3 = (х – 1)(х2 + 2х + 3)
Можно ли разложить на множители квадратный трехчлен х2 + 2х + 3? Попытаемся решить ур-ние
х2 + 2х + 3 = 0
D = b2– 4ас = 42 – 4•2•3 = 16 – 24 = – 8
Получили, что корней нет. Это значит, что функция у = х2 + 2х + 3 не пересекает ось Ох, и, так как коэффициент а этого трехчлена положителен, то выражение х2 + 2х + 3 больше нулю при любом х.
Это можно показать и иначе, если выделить полный квадрат из трехчлена:
х2 + 2х + 3 = х2 + 2х + 1 + 2 = (х + 1)2 + 2
Перепишем исходное нер-во с учетом разложения многочлена на множители:
х3 + 2х + 3 > 0
(х – 1)(х2 + 2х + 3) > 0
Так как выражение х2 + 2х + 3 положительно при любом значении х, то мы можем поделить неравенство на него:
х – 1 > 0
Отсюда получаем, что х∊(1; + ∞).
Ответ: (1; + ∞).
Пример. Укажите наименьшее целое решение неравенства
4х3 + 4х2 – 7х + 2 > 0
Решение. Попытаемся найти корень многочлена 4х3 + 4х2 – 7х + 2. Целый корень должен быть делителем двойки (свободного члена), то есть возможны варианты 1 и (–1), 2 и (– 2). Из них подходит только – 2:
4•(– 2)3 + 4•(– 2)2 – 7•(– 2) + 2 = – 32 + 16 + 14 + 2 = 0
Значит, можно поделить исходный многочлен на х + 2:
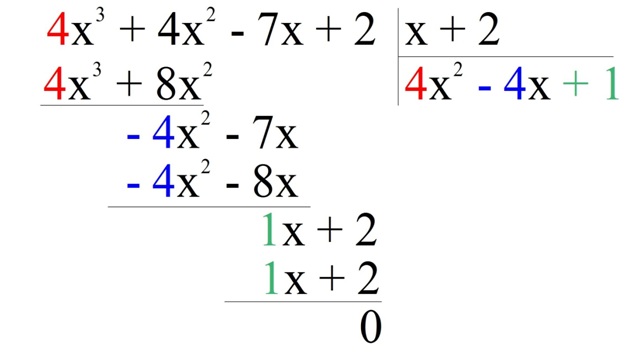
Можно записать, что 4х3 + 4х2 – 7х + 2 = (х + 2)(4х2 – 4х + 1).
Далее разложим получившийся при делении квадратный трехчлен на множители, для чего приравняем его к нулю:
4х2 – 4х + 1 = 0
D = b2– 4ас = (– 4)2 – 4•4•1 = 16 – 16 = 0
Получается, что есть лишь один корень.
х = – b/(2a) = – (– 4)/(2•4) = 0,5
Если у квадратного трехчлена дискриминант равен нулю, то это значит, что он является полным квадратом какого-то выражения. Действительно:
4х2 – 4х + 1 = (2х)2 – 2•2х•1 + 12 = (2х – 1)2
Тогда можно записать:
4х3 + 4х2 – 7х + 2 = (х + 2)(4х2 – 4х + 1) = (х + 2)(2х – 1)2 =
= (х + 2)(2х – 1)(2х – 1)
Перепишем с учетом этого исходное нер-во:
4х3 + 4х2 – 7х + 2 > 0
(х + 2)(2х – 1)(2х – 1) > 0
Вынесем множитель 2 из двух последних скобок и поделим нер-во на них:
(х + 2)•2•(х – 0,5)•2•(х – 0,5) > 0
(х + 2)(х – 0,5)(х – 0,5) > 0
Решим его методом интервалов:
Снова из-за двух одинаковых скобок (х – 0,5) на соседних промежутках (– 2; 0,5) и (0,5; 2) получили один и тот же знак. Функция положительна на них, однако она равна нулю при х = 0,5, поэтому это число из решения неравенства исключается. Получаем, что х∈(– 2; 0,5)∪(0,5; + ∞).
Нам надо указать наименьшее целое решение. Самым малым целым числом из множества (– 2; 0,5)∪(0,5; + ∞) является (– 1).
Ответ: (– 1).





























