Введение
Порядковые числа — это обобщение, которое расширяет последовательность натуральных чисел 1, 2, 3,… По этой причине, хотя порядковые числа являются собственно индуктивными множествами, они называются «числами». Все ординалы составляют класс , называемый Ord. Желательность этого обобщения следует из следующего наблюдения:
Кардинальные числа можно использовать для количественной оценки размера множества (конечного или бесконечного), а порядковые числа можно использовать для описания положения элемента в последовательности (конечной или бесконечной). Когда речь идет о конечных множествах, натуральные числа, ординалы и количественные числа совпадают, то есть они в основном идентифицируемы. В случае бесконечных множеств ситуация сложнее и необходимо различать порядковые и количественные (кроме того, для бесконечных множеств натуральные числа бесполезны). Аспект размера множества описывается количественными числами , которые также были открыты Кантором, в то время как аспект положения обобщается порядковыми числами, которые мы здесь обсуждаем.
В теории множеств натуральные числа обычно строятся как множества , так что каждое натуральное число является множеством всех меньших натуральных чисел:
С этой точки зрения каждое натуральное число представляет собой хорошо упорядоченный набор : например, набор из 4 состоит из элементов 0, 1, 2 и 3, которые, конечно же, упорядочены 0 < 1 < 2 < 3, и это хорошо. заказ. Одно натуральное число меньше другого тогда и только тогда, когда оно является элементом другого.
В соответствии с этим соглашением можно показать, что каждое хорошо упорядоченное конечное множество упорядоченно изоморфно ровно одному натуральному числу . Этот изоморфизм побуждает обобщить эту конструкцию на неконечные множества и соответствующие им числа, которые были бы больше любого натурального числа.
Порядковые номера
Порядковый номер – это число, которое указывает положение или порядок по отношению к другим числам: первое, второе, третье и т. д. Автор Марк Эндрю Лим определяет порядковые числа:
Порядковые числа прямо противоположны кардинальным числам (также называемым натуральными и целыми числами), которые представляют собой счетные количества.
Порядок обучения
Если вы преподаете порядковые номера изучающим английский язык или молодым студентам, представьте концепцию, просмотрев количественные числа, затем перейдите к порядковым номерам и сравните и сопоставьте эти две концепции. Будьте особенно внимательны, чтобы указать порядковые номера, которые нарушают шаблоны. Также введите термины first и last как словарные слова позиции.
Пример Порядковые числа
Все порядковые числа имеют суффикс: -nd, -rd, -st, или -th . Порядковые номера могут быть записаны как слова ( второй, третий ) или как цифры, за которыми следуют сокращения ( 2nd, 3rd ).
- 1: первый, первый
- 2: второй, второй
- 3: третий, третий
- 4: четвертый, четвертый
- 5: пятый, пятый
- 6: шестой, шестой
- 7: седьмое, 7-е
- 8: восьмое, 8-е
- 9: девятое, 9-е
- 10: десятое, 10-е
- 11: одиннадцатое, 11-е
- 12: двенадцатое, 12-е
- 20: двадцатое, 20-е
- 21: двадцать первое, 21-е
- 22: двадцать второе, 22-е
- 23: двадцать третье, 23-е
- 24: двадцать- четвертое, 24-е
- 30: тридцатое, 30-е
- 100: сотое, сотое
- 1000: одна тысячное, 1000-е
- 1 миллион: одна миллионная, 1,000,000-я
- 1 миллиард: одна миллиардная, 1,000,000,000-я
Как писать порядковые числа
Поскольку порядковые числа можно выразить словами или числами, бывает трудно определить, когда какую версию использовать. К счастью, автор Р. Риттер объясняет это в Правилах Нового Харта: Справочник по стилю для писателей и редакторов. “Укажите порядковые номера – первый, второй, третий, четвертый – за исключением случаев цитирования из другого источника. В интересах экономии места они также могут быть выражены цифрами в примечаниях и ссылках. …
«Используйте слова для порядковых номеров в названиях и для числовых названий улиц … :
- Третий Рейх
- Четвертый Estate
- пятый обозреватель
- Шестая авеню
- Седьмой -дневный адвентист …
Используйте цифры для возраста, выраженные в количественных числах, и слова для возрастов, выраженные в порядковых числах или десятилетиях:
- девочка 15 лет и 33-летний мужчина
- от подростка до двадцати
- в его 33-й год “(Риттер 2005).
Но, конечно же, порядковые номера можно использовать гораздо больше, чем просто названия улиц и возраст , а это означает больше правил. Вот еще несколько условий использования порядковых номеров, предоставленных экспертом по грамматике Вэлом Драмондом. “Не используйте порядковый номер ( th, st, rd , nd ) форма цифр при написании полной даты: 15 января – дата сдачи экзамена . Однако вы можете использовать порядковые суффиксы, если используете только день: 15-е число – это дата экзамена. …
Выпишите порядковые номера, если они содержат только одно слово: третье место, десятое место в строке, шестидесятая годовщина, пятнадцатилетие. Используйте цифры для остальных: 52-й штат, 21-я поправка »(Dumond 2012).
Использование порядковых и кардинальных чисел вместе
Порядковые и количественные числа часто встречаются вместе, даже для количественной оценки одного и того же объекта. Ауриэль Дуглас и Майкл Штрампф разбирают использование порядковых и количественных чисел вместе в своей книге Грамматическая Библия . “Когда кардинальное число и порядковое число изменяют одно и то же существительное, порядковое число всегда предшествует количественному числу: первые две операции были самыми сложными смотреть. вторые три иннинга были довольно скучными.
В первом примере порядковый номер first предшествует количественному числу два . Оба first и two являются определяющими. Во втором примере порядковое число секунда предшествует количественному числу три . И second , и three являются определяющими. Попробуйте читать предложения с перевернутыми порядковыми и количественными числами. Они просто звучат неправильно “(Дуглас и Стрампф, 2004).
Что такое числовая последовательность — понятие и определение
Последовательность представляет собой набор компонентов множества.
Последовательность обладает рядом отличительных признаков:
- каждый элемент из множества соотносится с натуральным числом;
- число используют для обозначения номера элемента и идентификации позиции этого компонента в рассматриваемой последовательности;
- для всех элементов можно определить следующий за ним компонент последовательности.
Предположим, что х является числовым множеством. Тогда можно использовать его в формулировке числовой функции.
https://youtube.com/watch?v=sQvrx6UFmf0
Числовая функция f является законом, согласно условиям которого, каждый элемент из х соответствует единственному числу.
Множество х в данном случае представляет собой область определения.
Числовая последовательность является функцией переменной n, принадлежащей множеству натуральных чисел N.
\(x_{n}=f\left(n \right)\)
С помощью функции можно определить любой член из последовательности. Этим свойством она отличается от произвольного комплекса чисел. В математике принято использовать буквы и числа для записи понятий и законов. Числовые последовательности, как правило, обозначают буквой х, хотя строгих правил на этот счет не предусмотрено.
\(x_{n}=f\left(n \right)\)
\(x_{1},x_{2},x_{3},x_{4},…x_{n},…\)
1.8. Множество¶
Множество — это изменяемый неупорядоченный тип данных. В множестве всегда содержатся только уникальные элементы.
Множество в Python — это последовательность элементов, которые разделены между собой запятой и заключены в фигурные скобки.
С помощью множества можно легко убрать повторяющиеся элементы:
cities = 'Санкт-Петербург', 'Хабаровск', 'Казань', 'Санкт-Петербург', 'Казань'
un_cities = set(cities)
for city in un_cities
print("Один мой друг живёт в городе " + city)
'''
Один мой друг живёт в городе Хабаровск
Один мой друг живёт в городе Санкт-Петербург
Один мой друг живёт в городе Казань
'''
Множества полезны тем, что с ними можно делать различные операции и находить объединение множеств, пересечение и так далее.
Объединение множеств можно получить с помощью метода union() или оператора :
vlans1 = {10,20,30,50,100}
vlans2 = {100,101,102,102,200}
vlans1.union(vlans2) #{10, 20, 30, 50, 100, 101, 102, 200}
vlans1 | vlans2 #{10, 20, 30, 50, 100, 101, 102, 200}
#Пересечение множеств можно получить с помощью метода intersection() или оператора &
vlans1 = {10,20,30,50,100}
vlans2 = {100,101,102,102,200}
vlans1.intersection(vlans2) #{100}
vlans1 & vlans2 #{100}
Вещественные типы
Значения вещественных типов в компьютере представляются приближенно. Диапазон изменения данных вещественного типа определяется пятью стандартными типами: вещественный ( Real ), с одинарной точностью ( Single ), двойной точностью ( Double ), с повышенной точностью ( Extended ), сложный ( Comp ) и представлен в таблице:
| Тип | Диапазон | Число значащих цифр | Размер в байтах |
| Real | 2.9E-39…1.7E+38 | 11-12 | 6 |
| Single | 1.5E-45…3.4E+38 | >7-8 | 4 |
| Double | 5E-324…1.7E+308 | 15-16 | 8 |
| Extended | 3.4E-4951…1.1E+4932 | 19-20 | 10 |
| Comp | -2E+63+1…+2E+63-1 | 19-20 | 8 |
Вещественные числа могут быть представлены в двух форматах: с фиксированной и плавающей точкой.
Формат записи числа с фиксированной точкой совпадает с обычной математической записью десятичного числа с дробной частью. Дробная часть отделяется от целой части с помощью точки, например
34.5, -4.0, 77.001, 100.56
Формат записи с плавающей точкой применяется при записи очень больших или очень малых чисел. В этом формате число, стоящее перед символом «E», умножается на число 10 в степени, указанной после символа «E».
| 1E-4 | 1*10-4 |
| 3.4574E+3 | 3.4574*10+3 |
| 4.51E+1 | 4.51*10+1 |
Примеры чисел с плавающей точкой:
| Число | Запись на Паскале |
| 0,0001 | 1E-4 |
| 3457,4 | 34574E-1 |
| 45,1 | 451E-1 |
| 40000 | 4E+4 |
| 124 | 0.124E+3 |
| 124 | 1.24E+2 |
| 124 | 12.4E+1 |
| 124 | 1240E-1 |
| 124 | 12400E-2 |
В таблице с 5 по 9 строку показана запись одного и того же числа 124. Изменяя положение десятичной точки в мантиссе (точка «плывет», отсюда следует название «запись числа с плавающей точкой») и одновременно изменяя величину порядка, можно выбрать наиболее подходящую запись числа.
Пример описания переменных вещественного типа.
Var
x,y,z:real;
Порядковый номер химического элемента
Заря́довое число́ атомного ядра (синонимы: атомный номер, атомное число, порядковый номер химического элемента) — количество протонов в атомном ядре. Зарядовое число равно заряду ядра в единицах элементарного заряда и одновременно равно порядковому номеру соответствующего ядру химического элемента в таблице Менделеева.
Термин «атомный» или «порядковый» номер обычно используется в атомной физике и химии, тогда как эквивалентный термин «зарядовое число» — в физике ядра. В неионизированном атоме количество электронов в электронных оболочках совпадает с зарядовым числом.
Зарядовое число обычно обозначается буквой Z. Ядра с одинаковым зарядовым числом, но различным массовым числом A (которое равно сумме числа протонов Z и числа нейтронов N) являются различными изотопами одного и того же химического элемента, поскольку именно заряд ядра определяет структуру электронной оболочки атома и, следовательно, его химические свойства.
Смотреть что такое «Порядковый номер химического элемента» в других словарях:
ПОРЯДКОВЫЙ НОМЕР — элемента, то же, что (см. АТОМНЫЙ НОМЕР). Физический энциклопедический словарь. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983. ПОРЯДКОВЫЙ НОМЕР … Физическая энциклопедия
ПОРЯДКОВЫЙ НОМЕР — химического элемента то же, что атомный номер … Большой Энциклопедический словарь
Порядковый номер элемента — Зарядовое число атомного ядра (синонимы: атомный номер, атомное число, порядковый номер химического элемента) количество протонов в атомном ядре. Зарядовое число равно заряду ядра в единицах элементарного заряда и одновременно равно порядковому… … Википедия
порядковый номер — химического элемента, то же, что атомный номер. * * * ПОРЯДКОВЫЙ НОМЕР ПОРЯДКОВЫЙ НОМЕР химического элемента, то же, что атомный номер (см. АТОМНЫЙ НОМЕР) … Энциклопедический словарь
Атомный номер — порядковый номер химического элемента в периодической системе элементов (См. Периодическая система элементов) Д. И. Менделеева. А. н. равен числу протонов в атомном ядре, которое, в свою очередь, равно числу электронов в электронной… … Большая советская энциклопедия
АТОМНЫЙ НОМЕР — АТОМНЫЙ НОМЕР, порядковый номер химического элемента в периодической системе элементов. Равен числу протонов в атомном ядре, определяет химические и большинство физических свойств атома … Современная энциклопедия
Атомный номер — АТОМНЫЙ НОМЕР, порядковый номер химического элемента в периодической системе элементов. Равен числу протонов в атомном ядре, определяет химические и большинство физических свойств атома. … Иллюстрированный энциклопедический словарь
атомный номер — порядковый номер, Z, номер химического элемента в периодической системе элементов. Равен числу протонов в атомном ядре и определяет химические и большинство физических свойств атома. * * * АТОМНЫЙ НОМЕР АТОМНЫЙ НОМЕР (порядковый номер), Z, номер… … Энциклопедический словарь
АТОМНЫЙ НОМЕР — (порядковый номер) Z, номер химического элемента в периодической системе элементов. Равен числу протонов в атомном ядре и определяет химические и большинство физических свойств атома … Большой Энциклопедический словарь
Химический элемент — Химический элемент совокупность атомов с одинаковым зарядом ядра и числом протонов, совпадающим с порядковым (атомным) номером в таблице Менделеева. Каждый химический элемент имеет свои название и символ, которые приводятся в… … Википедия
Окружения
Окружения — это хеш-таблицы, то есть пары ключ-значение. Значениями обычно являются объявленные функции, данные, другие окружения. Окружения похожи на , но сходство только внешнее, так как окружения, в отличие от списков, не имеют порядок объектов (соответственно, объекты окружения нельзя вызвать по их номеру, как в листе) и ансамбль окружений может быть представлен в виде дерева — практически у любого окружения есть родительское окружение.
За пределами функций использование окружений достаточно ограничено. Как правило, это либо ситуативные модификации функций пакетов, либо эзотерические практики организации объектов в интерактивном рабочем пространстве. Однако у окружений есть одна нечасто используемая характеристика: можно использовать окружения именно как хеш-таблицы, в которых операции поиска, вставки или удаления по ключам значений (названию) осуществляются в среднем быстрее, чем по обычным таблицам.
Например, создадим два объекта — таблицу, в которой в одной колонке будет вектор — текстовых значений, а во второй — числовое значение (). Второй объект — хешированное окружение с таким же количеством объектов, как строк в таблице. Каждый объект этого окружения имеет название, соответствующее значениям в первой колонке таблицы, а значения объектов — значениям из второй колонки таблицы ( для всех объектов, как и для всех строк таблицы).
Как можно увидеть по бенчмаркам, поиск значения определённого объекта в хешированном окружении существенно быстрее поиска соответствующих значений в таблице:
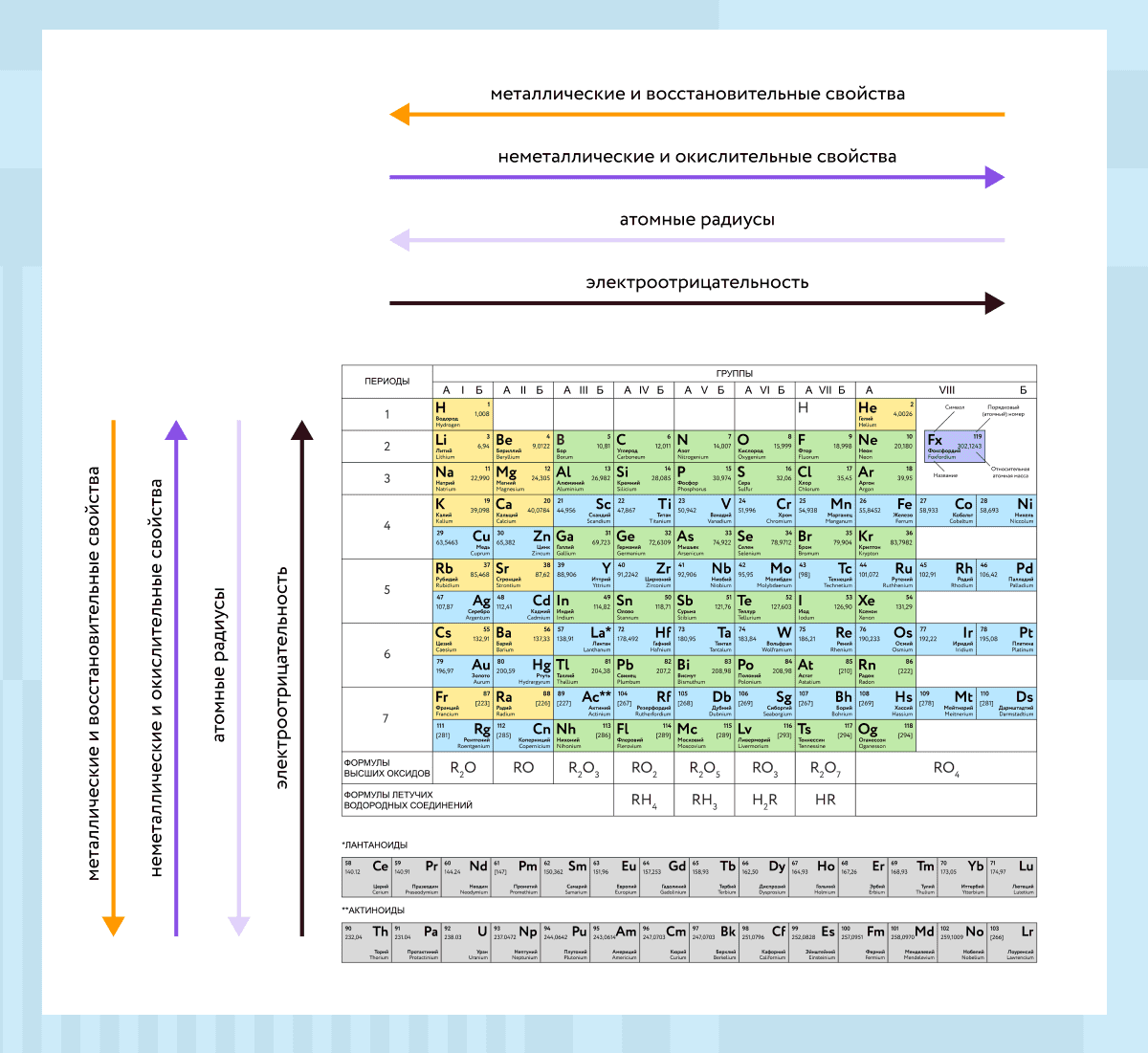
Свойства Периодической системы элементов
Расположение химических элементов в таблице Менделеева позволяет сопоставлять не только их атомные массы, но и химические свойства.
Вот как они изменяются в пределах группы (сверху вниз):
- Металлические свойства усиливаются, неметаллические ослабевают.
- Увеличивается атомный радиус.
- Усиливаются основные свойства гидроксидов и кислотные свойства водородных соединений неметаллов.
В пределах периодов (слева направо) свойства элементов меняются следующим образом:
- Металлические свойства ослабевают, неметаллические усиливаются.
- Уменьшается атомный радиус.
- Возрастает электроотрицательность.
Вопрос-ответ:
Что такое порядковый номер?
Порядковый номер — это числовое значение, которое используется для упорядочивания элементов в некотором наборе. Он указывает позицию элемента в этом наборе относительно других элементов.
Как использовать порядковый номер?
Порядковый номер можно использовать для доступа к определенному элементу в наборе. Например, в массиве можно получить элемент по его порядковому номеру, используя индексацию. Порядковый номер также может быть использован для определения положения элемента в ранжированных списках или для упорядочивания данных при сортировке.
Можно ли использовать отрицательный порядковый номер?
В большинстве случаев порядковый номер начинается с 0 для первого элемента и увеличивается на 1 для каждого следующего элемента. Однако, в некоторых языках программирования, таких как Python, можно использовать отрицательные порядковые номера, которые считаются с конца набора. Например, -1 обозначает последний элемент, -2 — предпоследний, и так далее.
Можно ли использовать нецелые числа в качестве порядковых номеров?
В общем случае порядковый номер представляет собой целое число, обозначающее позицию элемента в наборе. Нецелые числа обычно не используются в качестве порядковых номеров, поскольку позиции обычно являются дискретными значениями. Однако, в некоторых случаях, например, при работе с таблицами или списками с плавающей точкой, может быть возможно использование нецелых чисел в качестве порядковых номеров.
Может ли порядковый номер изменяться?
В большинстве случаев порядковый номер является статичным значением и не изменяется для элемента в наборе. Однако, в некоторых ситуациях порядковый номер может быть изменен, например, при удалении или вставке элементов. При удалении элемента порядковые номера последующих элементов могут измениться, а при вставке нового элемента его порядковый номер будет зависеть от его положения в наборе.
Что такое порядковый номер?
Порядковый номер — это числовое обозначение позиции элемента в определенной последовательности. Он позволяет определить положение элемента относительно других элементов.
Зачем нужен порядковый номер?
Порядковый номер используется для упорядочивания и классификации элементов в различных областях. Он помогает определить положение элемента в списке, ранжировать данные и упростить процесс сортировки и поиска.
Порядковый номер: общее понятие
Порядковые номера могут быть использованы в различных ситуациях и представлены в разных форматах. Например, в некоторых языках программирования порядковый номер может быть использован для доступа к элементам массива или списка. В таблицах баз данных порядковый номер может использоваться для идентификации и сортировки записей.
Один из примеров использования порядкового номера — нумерация страниц в книге или документе. Каждая страница имеет свой уникальный порядковый номер, который позволяет читателю легко найти нужную страницу и ориентироваться в тексте.
Определение порядкового номера
Порядковый номер может быть присвоен элементам в различных контекстах, таких как списки, таблицы, базы данных и другие. Он обычно начинается с 1 и увеличивается на единицу для каждого следующего элемента.
Порядковые номера позволяют легко ссылаться на определенные элементы в коллекции при помощи их уникального числового идентификатора. Например, в нумерованном списке каждый элемент может быть идентифицирован своим порядковым номером, что упрощает ссылки на него.
| Элемент | Порядковый номер |
|---|---|
| Элемент 1 | 1 |
| Элемент 2 | 2 |
| Элемент 3 | 3 |
| Элемент 4 | 4 |
В приведенной выше таблице показан пример порядковых номеров для элементов в коллекции. Каждый элемент имеет свой уникальный порядковый номер, который может быть использован для ссылки на него или выполнения других операций, связанных с его позицией в коллекции.
Использование порядкового номера
Одним из основных способов использования порядкового номера является создание нумерованных списков. Он позволяет структурировать информацию, выделять ключевые пункты и помогает читателям легче ориентироваться в тексте.
Пример использования порядкового номера:
Этот код создаст нумерованный список с тремя пунктами. Каждому пункту будет автоматически присвоен порядковый номер: 1, 2 и 3 соответственно.
Порядковый номер также может использоваться в CSS для добавления стилей к определенным элементам. Например, можно изменить цвет или размер текста у пунктов списка с определенными порядковыми номерами:
Этот код изменит цвет текста и размер шрифта у второго пункта нумерованного списка.
Использование порядкового номера позволяет более гибко управлять структурой и внешним видом элементов в HTML-коде, делая его более понятным и удобным для чтения и использования.
Примеры использования порядкового номера
1. Нумерация элементов в списке
Порядковый номер может быть использован для нумерации элементов в списке. Например, мы можем создать список стран, указав порядковый номер перед названием каждой страны:
- Россия
- США
- Китай
- Индия
2. Упорядочивание задач в списке
Порядковый номер также может быть использован для упорядочивания задач в списке дел или заданий. Например, мы можем создать список заданий для студентов и пронумеровать их:
- Прочитать главу 1 учебника
- Написать эссе на заданную тему
- Подготовить презентацию
- Сдать контрольную работу
3. Показ последовательности действий
Порядковый номер может быть использован для показа последовательности действий или шагов в инструкции или руководстве. Например:
- Откройте меню «Настройки»
- Выберите пункт «Сеть»
- Нажмите на кнопку «Подключение к сети»
- Введите пароль и нажмите кнопку «Подтвердить»
Все эти примеры демонстрируют различные способы использования порядкового номера для нумерации элементов и обозначения последовательности действий. Порядковый номер является важным инструментом, который помогает представлять информацию в структурированной и упорядоченной форме.
Формулы
На данный момент формулы — специальный объект, который описывает схему взаимодействия зависимой переменной (таргета) и независимых переменных (предикторов), а также взаимодействие предикторов между собой. Формульная нотация для записи регрессионной модели предложена Роджерсом и Вилкинсоном в 1973 году (), позднее её включили в язык () и, следовательно, она попала в . Простой пример формулы, описывающий одну зависимую переменную и две независимые:
Слева от знака тильды находится зависимая переменная (LHS, left-hand side). В стандартном использовании слева только одна переменная, если же необходимо указать несколько зависимых и/или их взаимодействие, то следует воспользоваться соответствующими пакетами. Справа от тильды, right-hand side (RHS), — две независимые переменные. Знак в формулах означает независимое влияние переменных. По сути, формульная нотация — это своего рода DSL внутри R, так как в нотации привычные знаки и операторы имеют собственное значение:
-
используется для того, чтобы перечислить переменные-предикторы;
-
используется, чтобы указать, влияние какого фактора необходимо исключить из модели;
-
передаёт в качестве предиктора модели только взаимодействие факторов (аналогично );
-
задаёт как изолированное влияние каждого фактора, так и их взаимодействие (аналогично );
-
используется в тех ситуациях, когда необходимо ввести в модель случайные эффекты;
-
или в формуле указывает, что из модели следует исключить случайный член (intercept);
-
позволяет указывать в качестве предикторов все колонки в таблице, помимо зависимой переменной.
Легче всего показать разницу в формулах с помощью простейшей линейной регрессии. Создадим несколько переменных, из которых разными методами сконструируем зависимую переменную:
Создадим зависимую исходя из возможных вариантов взаимодействия предикторов. Следует помнить, что знак в обычном выражении и в формуле интерпретируется по-разному.
Зададим и применим модель ( означает взаимодействие факторов). Модель должна вычислить заданные нами коэффициенты, которые мы использовали при создании вектора :
Аналогичный результат можно получить, если задать модель не через , а через и :
Так как поведение операторов в формулах иное, чем в обычных выражениях, то при необходимости использовать в формуле собственно сложение или другие операции, следует воспользоваться функцией (от ):
Формулу можно создать несколькими путями: просто создать текстовую переменную либо же воспользоваться функцией , в конце концов, можно просто написать . Результаты потом можно использовать в соответствующих функциях. Текстовое описание модели в формуле позволяет создавать генераторы моделей (например, при переборе комбинаций предикторов в машинном обучении). Пример случайной генерации моделей, сочетающих два независимых предиктора и взаимодействие ещё двух предикторов:
Формулы обычно используются в линейных моделях, случайных лесах и многих других функциях, в которых требуется описание модели взаимосвязи нескольких переменных. Так как тильда в формулах обозначает, что ничего не надо вычислять и надо просто запомнить выражение и его окружение, возможны и другие варианты использования формул. Например, помимо соотношения таргета и предикторов, тильда и формульная нотация может использоваться для определения формы взаимодействия колонок при решейпинге таблиц. Подобное использование встречается и в других пакетах:
Строение периодической системы
Для начала рассмотрим понятия таблица и система. Вы не один раз видели таблицу, она состоит из строк и столбцов. Но почему творение Менделеева имеет названия как таблица, так система да еще и с добавлением периодическая.
В таблице содержится упорядоченная информация в определённом порядке. Система указывает, что сведения связаны между собой. Периодичность означает, что через какой-то промежуток или отрезок происходит повторение свойств.
Как уже известно, в периодической системе находятся элементы. Принцип их расположения — это увеличение их атомной массы.
В таблице имеются строки – это периоды, и столбцы – группы.
Существует несколько вариантов ПСХЭ, так называемый короткий и длинный вариант.
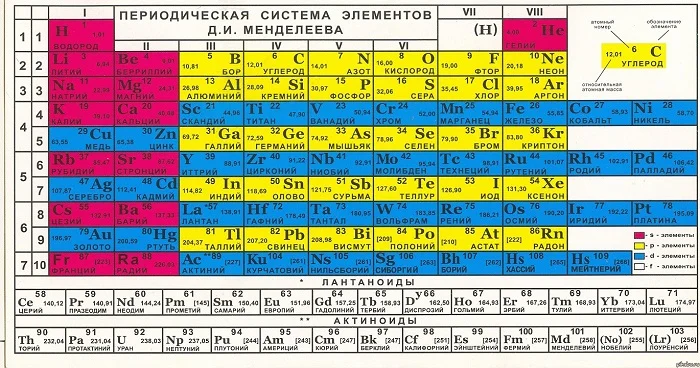
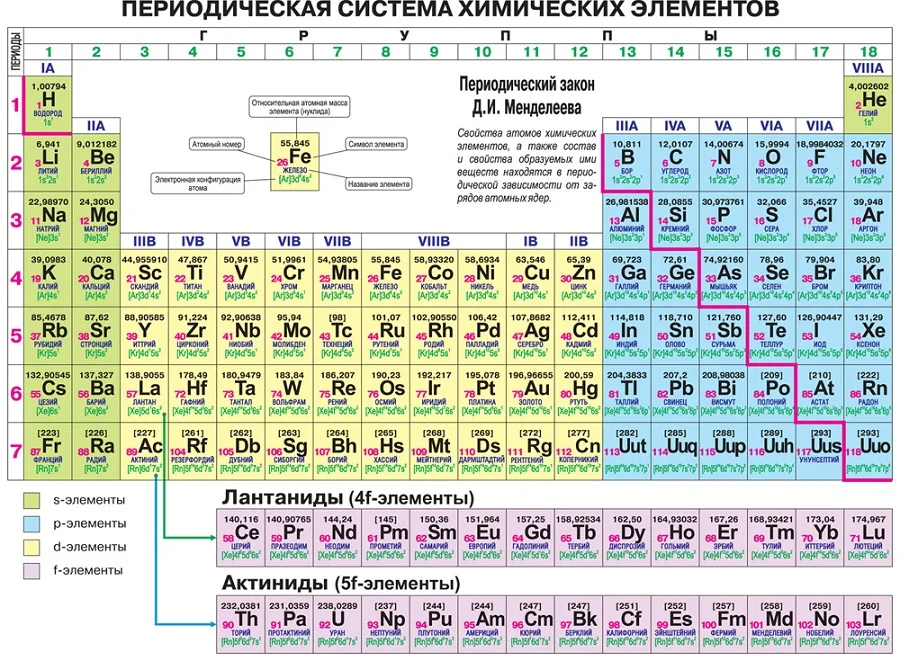
Короткий вариант имеет 8 групп, номера которых указаны римскими цифрами I, II…VIII, содержит главную (А) и побочную (В) группы. Длинный формат вмещает 18 групп, нумерация осуществляется арабскими цифрами I, II…XVIII,
Если посмотреть на таблицу, то видим закономерность, так как абсолютно каждый период будет начинаться активным металлом и заканчиваться инертным газом. Такая периодичность сохраняется 7 раз.
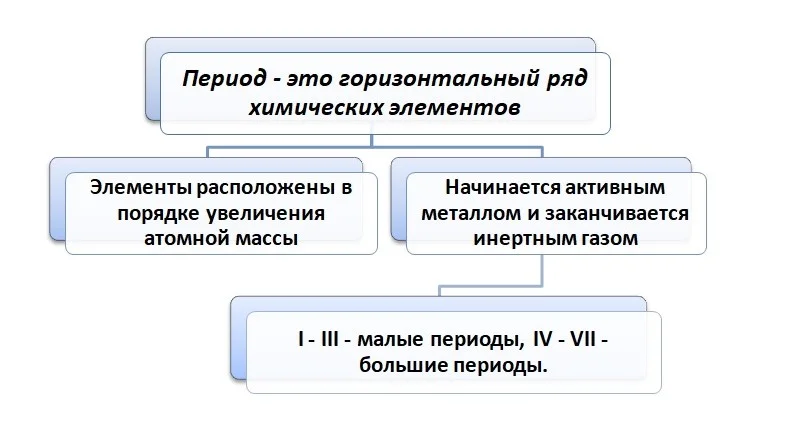
Как видно из таблицы, I период включает 2 элемента, II и III состоят из 8, IV и V содержат 18, самые большие – это VI и VII вмещают 32 элемента (VII период незаконченный).
В периоде с ростом атомной массы металлические свойства уменьшаются, неметаллические – увеличиваются.
Вертикальные столбцы образуют группы. Это условно компании, где собираются единомышленники. Точнее, располагаются элементы, подобные по своим свойствам.

Обратите внимание, что подобие характерно только в пределах подгруппы. Так, натрий и медь принадлежат одной I группе, но располагаются в разных подгруппах. Натрий – элемент главной подгруппы, медь – побочной
Именно по этой причине они будут иметь разные физические и химические свойства
Натрий – элемент главной подгруппы, медь – побочной. Именно по этой причине они будут иметь разные физические и химические свойства.
В пределах группы с ростом атомной массы металлические свойства увеличиваются, неметаллические – уменьшаются.
Таким образом, периодическую систему можно условно назвать домом химических элементов, где каждый из них занимает своё определённое место (порядковый номер) согласно его свойствам.


Рассмотрим подробнее на примере 2 и 3 периода. Что показывает сравнение: оба периода начинаются с активных металлов Li и Na, для которых характерно существование в виде соединений, в свободном виде могут находиться только под слоем керосина. Они относятся к группе щелочных металлов. Анализируя схему, мы видим, что первые три группы образованны металлами. С IV – VII находятся неметаллы. «Закрывают период» инертные газы.
Особое внимание располагают к себе элементы VI и VII периоды, которые образуют «семейство» лантаноидов (Лантан № 57) и актиноидов (Актиний 89), они формально близки к скандию. Но из-за их количества они вынесены за пределы системы
Способы задания числовых последовательностей
Такие действия можно выполнять по-разному. К основным способам задания последовательностей относят:
- аналитический или с помощью формулы;
- реккурентный, при наличии нескольких известных первых элементов прогрессии и формулы для определения следующих членов последовательности;
- описательный, включает простое перечисление всех компонентов последовательности.
Аналитический способ задания числовой последовательности
Считают, что последовательность задана аналитически, когда представлено уравнение для расчета ее n-го элемента.
\(y_{n}=f(n)\)
В качестве примера можно рассмотреть:
\(y_{n}=\frac{1}{n}\)
Это аналитический способ задания последовательности чисел:
\(1;\frac{1}{2};\frac{1}{3};…\frac{1}{n};…\)
Зная конкретное значение n, можно определить элемент последовательности с соответствующим номером. Можно изобразить данную последовательность на графике. Исходя из определения графика функции, он будет представлять собой множество всех точек:
\((n;\frac{1}{n})\)
Указанные точки будут расположены на правой ветви гиперболы:
\(y=\frac{1}{x}\)
Функция \(y=\frac{1}{x}\) в случае, когда x > 0, будет убывающей. В таком случае числовая последовательность \(y_{n}=\frac{1}{n}\) также будет убывать.
Можно рассмотреть второй пример, когда:
\(y_{n}=\left|n-5 \right|\)
Следует представить несколько элементов данной числовой прогрессии:
\(y_{1}=\left|1-5 \right|=4\)
\(y_{2}=\left|2-5 \right|=3\)
\(y_{3}=\left|3-5 \right|=2\)
Графиком рассматриваемой последовательности будет являться множество точек, которые характеризуются координатами:
\((n;\left|n-5 \right|)\)
Эти точки принадлежат ломаной линии:
\(y=\left|x-5 \right|\)
Числовая последовательность \(y_{n}=\left|n-5 \right|\) будет убывать, если n соответствует интервалу от 1 до 5, и возрастать – при n от 5 до бесконечности.
Описательный метод задания числовой последовательности
Данная методика используется не всегда. Описательный способ записи последовательности чисел целесообразно применять, когда в условии задачи отсутствуют формулы, а правило прогрессии изложено лишь словами. В качестве примера можно рассмотреть такую последовательность, в которой:
\(a_{n}\) является цифрой после запятой в десятичной записи числа \(\sqrt{2}\)
\(\sqrt{2}=1,41421…\)
\(a_{1}=4\); \(a_{2}=1\);\(a_{3}=4\);\(a_{4}=2\);\(a_{5}=1\);…
Порядковый номер — число
Порядковый номер числа в упорядоченном ряду называется рангом этого числа. Каждое число имеет два ранга, так как отсчет можно вести с двух концов числового ряда.
Для каждого значения п определяется порядковый номер числа г 0 числовой последовательности, наиболее близкий к абсциссе центра тяжести информационного поля, но меньший се.
Введем следующие обозначения: i — порядковый номер числа в последовательности ( 1 1 20); 5 — наибольшее по модулю число.
|
Передняя панель и программа отображения случайных чисел. |
Цифры на временной оси графика соответствуют порядковому номеру отображаемого числа, а скорость их обновления при непрерывном запуске связана только со временем выполнения операций перед выводом точки на график. После остановки программы значения на оси X графика сохраняются и при новом запуске график продолжается с прерванной позиции.
|
Структурная схема быстродействующего печатающего устройства. |
Кроме цифровых дорожек имеются знаковые дорожки и цифровые дорожки порядкового номера числа.
А ( я 1) А ( я) А ( я-1), где в скобках указан порядковый номер числа в ряде.
В соответствии с этим теперь можно сформулировать правило кодирования элементов информации, входящих в арифметические формулы: код каждого элемента информации состоит из двух частей; первая часть содержит код вида информации — число, операцию или знак равенства; вторая часть кода числа содержит порядковый номер числа; вторая часть кода операции в свою очередь разделяется на две части: одна содержит код одноместной ( pi) или код двуместной операции ( а), вторая — номер операции; вторая часть знака равенства свободна.
В результате на пленке записываются цифры в виде кодовых групп. Порядковый номер числа определяет его временную координату.
К борьбе с ошибками ввода и вывода можно отнести целый набор специальных приемов, повышающих надеж — ность работы оператора с программой. Хорошо сделать так, чтобы программа сама подсказывала оператору порядковый номер числа, которое должно быть введено
Что она вызовет на индикатор, не очень-то важно. Следующей командой на индикатор будет вызвано содержимое регистра 4, после чего калькулятор остановится
С каждым повторением этой цепочки на индйка торе будут появляться последовательно нарастающие це лые числа, под которыми можно понимать порядковые но-11 мера вводимых величин и в соответствии с такими подсказками эти величины и набирать на клавиатуре.
В справочных таблицах имеются готовые числовые значения ( пи) 0 — 3, но не все из них равны предпочтительным числам. Объясняется это тем, что возведенное в дробную положительную или отрицательную степень число будет предпочтительным только в том случае, если произведение порядкового номера числа на дробный показатель степени окажется целым числом.
Для расчета требуется твердо знать число элементов в каждом периоде и ряду. Зная это, определяют период, ряд и группу, последовательно вычитая из порядкового номера числа элементов в периодах и рядах, начиная с 1 периода и 1 ряда до тех пор, пока разность не окажется меньше числа элементов в следующем периоде. Обратный расчет — определение порядкового номера элемента по месту, занимаемому им в периодической системе, — производится путем сложения числа, показывающего место элемента в последнем периоде, с числом элементов в предыдущих периодах.




























