Введение в функции и алгебраический метод
Функции являются фундаментальной концепцией в математике, которую можно использовать для моделирования реальных явлений.Они являются ключевым инструментом в анализе и понимании сложных систем и используются в широком спектре областей, включая инженерию, физику и экономику.Одним из наиболее распространенных способов анализа функций является алгебраический метод, который включает в себя использование алгебраических операций для манипулирования уравнениями и разрешения для неизвестных переменных.Этот метод является мощным инструментом для анализа функций, поскольку он позволяет нам идентифицировать закономерности и отношения между различными переменными и делать прогнозы о том, как эти переменные будут изменяться с течением времени.
Вот некоторые ключевые идеи о внедрении функций и алгебраическом методе:
1. Функции — это математические объекты, которые связывают один набор значений с другим.Они могут быть представлены графически, алгебраически или численно, и могут использоваться для моделирования широкого диапазона явлений.
2. Алгебраический метод включает использование алгебраических операций, таких как добавление, вычитание, умножение и деление, для манипулирования уравнениями и решают неизвестные переменные.Этот метод особенно полезен для анализа функций, поскольку он позволяет нам идентифицировать закономерности и отношения между различными переменными.
3. Функции могут быть представлены алгебраически различными способами, включая использование уравнений, графиков или таблиц.Каждое из этих представлений обеспечивает другой способ понимания функции и может использоваться для анализа его свойств и поведения.
4. Одной из ключевых понятий в алгебраическом методе является идея домена и диапазона функции.Домен функции относится к набору входных значений, для которых определяется функция, в то время как диапазон относится к набору выходных значений, которые может создать функция.
5
При анализе функций с использованием алгебраического метода важно обратить внимание на свойства функции, такие как его симметрия, перехваты и асимптоты.Эти свойства могут дать важную информацию о поведении функции и могут быть использованы для прогнозирования его поведения с течением времени
6. Алгебраический метод может быть использован для решения широкого спектра проблем, включающих функции, включая поиск корней, определение наклона кривой и выявление критических точек.Используя этот метод, мы можем получить более глубокое понимание того, как работают функции и как их можно использовать для моделирования реальных явлений.
В целом, алгебраический метод является мощным инструментом для анализа функций и понимания их поведения.Используя алгебраические операции для манипулирования уравнениями и решения для неизвестных переменных, мы можем получить более глубокое понимание того, как работают функции и как их можно использовать для моделирования реальных явлений.
Введение в функции и алгебраический метод — Функции: применение алгебраического метода для анализа функций
Источники внешней и внутренней информации
Внешние источники информации могут быть различными и варьироваться в зависимости от конкретной ситуации. Вот некоторые из наиболее распространенных источников внешней информации:
- Базы данных — информация может быть извлечена из таблиц базы данных, используя SQL-запросы.
- Файлы — информация может быть прочитана из текстовых файлов, CSV-файлов, JSON-файлов и других форматов данных.
- API — информация может быть получена через API (Application Programming Interface) различных веб-служб, таких как социальные сети, погодные сервисы, картографические сервисы и другие.
- Сеть — информация может быть получена через сетевое взаимодействие с удаленными серверами, например, по протоколу HTTP.
Некоторые источники внутренней информации могут быть следующими:
- Переменные — функция может использовать уже определенные переменные для выполнения своей задачи.
- Аргументы — функция может принимать аргументы, которые передаются ей при ее вызове, и использовать их в своем коде.
- Результаты других функций — функция может получать информацию из результатов выполнения других функций, которые вызываются внутри нее.
Использование внешних источников информации требует особой осторожности и проверки наличия данных перед их использованием. Необходимо учитывать возможность ошибок в полученных данных и применять соответствующие механизмы обработки исключений
Задать функцию графиком
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.
График функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числовые значения вместо «x».
Пример. Дана функция: y(x) = −2x + 1.
Найти: значения «y» для произвольных «x», а именно −1, 0, 1.
Как рассуждаем:
1. Подставим данные значения х в функцию и запишем результаты:
|
x |
Рассчет |
|
−1 |
y(−1) = −2 * (−1) + 1 = 2 + 1 = 3 |
|
y(0) = −2 * 0 + 1 = 0 + 1 = 1 |
|
|
1 |
y(1) = −2 * 1 + 1 = −2 + 1 = −1 |
2. Каждая пара значений «x» и «y» — это координаты точек по оси Ox (абсцисса точки) и Oy (ордината точки).
Дадим названия каждой точке и запишем их координаты:
|
Имя точки |
x |
y |
|
A |
−1 |
3 |
|
B |
1 |
|
|
C |
1 |
−1 |
3. Отметим точки А (-1; 3), B (0; 1) и С (1; -1) на прямоугольной системе координат.
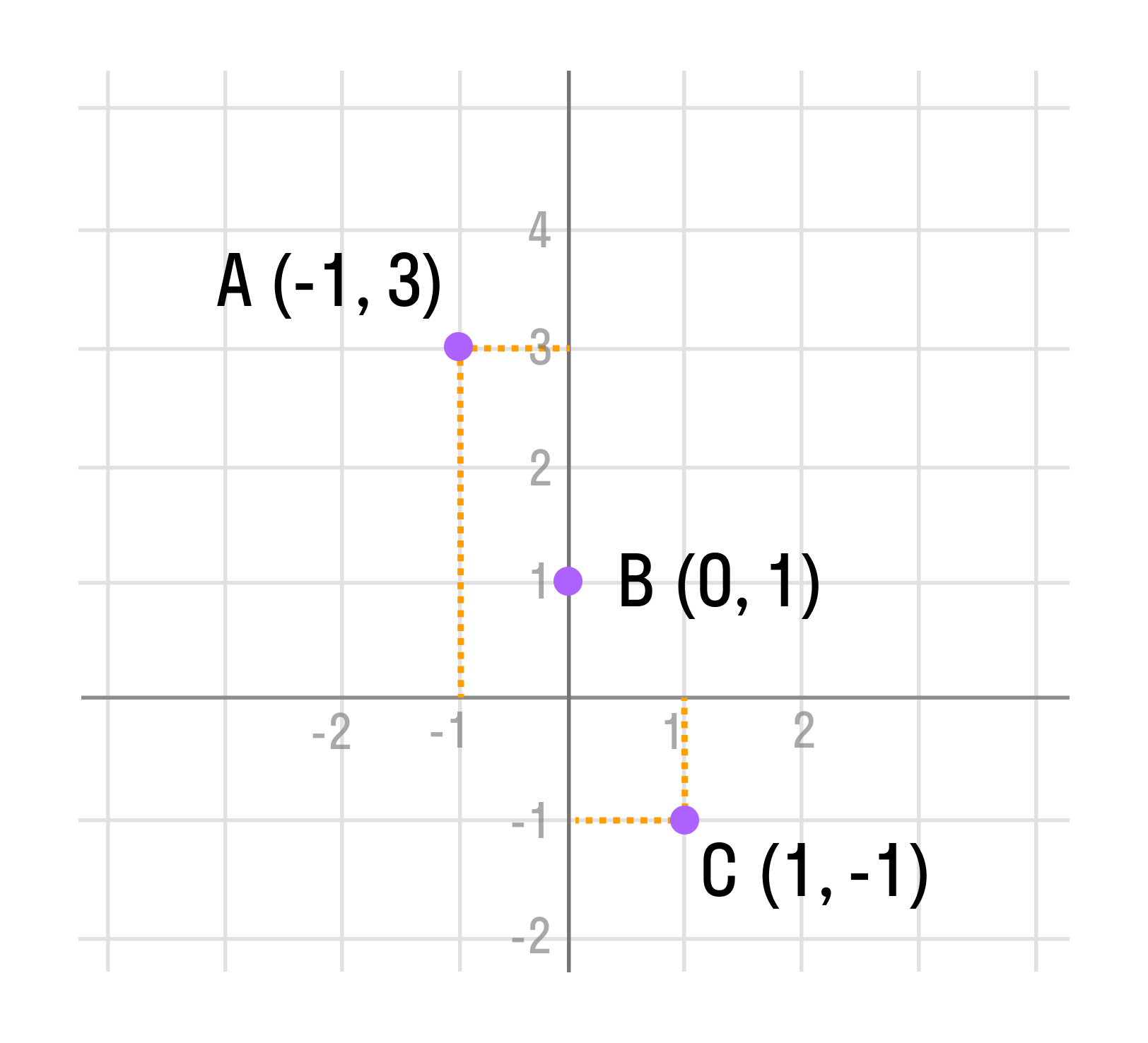
4. Соединим отмеченные точки прямой.
Проведенная прямая будет графиком функции y(x) = −2x + 1.
Функция. Способы задания функций.
Функция является заданной, иначе говоря, известной, если для каждого значения возможного числа аргументов можно узнать соответствующее значение функции. Наиболее распространенные три способа задания функции: табличный, графический, аналитический, существуют еще словесный и рекурсивный способы.
1. Табличный способ наиболее широко распространен (таблицы логарифмов, квадратных корней), основное его достоинство – возможность получения числового значения функции, недостатки заключаются в том, что таблица может быть трудно читаема и иногда не содержит промежуточных значений аргумента.
Аргумент х принимает заданные в таблице значения, а у определяется соответственно этому аргументу х.
2. Графический способ заключается в проведении линии (графика), у которой абсциссы изображают значения аргумента, а ординаты – соответствующие значения функции. Часто для наглядности масштабы на осях принимают разными.
Например: для нахождения по графику у, которому соответствует х = 2,5 необходимо провести перпендикуляр к оси х на отметке 2,5. Отметку можно довольно точно сделать с помощью линейки. Тогда найдем, что при х = 2,5 у равно 7,5, однако если нам необходимо найти значение у при х равном 2,76, то графический способ задания функции не будет достаточно точным, т.к. линейка не дает возможности для столь точного замера.
Достоинства этого способа задания функций заключаются в легкости и целостности восприятия, в непрерывности изменения аргумента; недостатком является уменьшение степени точности и сложность получения точных значений.
3. Аналитический способ состоит в задании функции одной или несколькими формулами. Основным достоинством этого способа является высокая точность определения функции от интересующего аргумента, а недостатком является затрата времени на проведение дополнительных математических операций.
Функцию можно задать с помощью математической формулы y=x 2 , тогда если х равно 2, то у равно 4, возводим х в квадрат.
4. Словесный способ состоит в задании функции обычным языком, т.е. словами. При этом необходимо дать входные, выходные значения и соответствие между ними.
Словесно можно задать функцию (задачу), принимающуюся в виде натурального аргумента х с соответствующим значением суммы цифр, из которых состоит значение у. Поясняем: если х равно 4, то у равно 4, а если х равно 358, то у равен сумме 3 + 5 + 8, т. е 16. Далее аналогично.
5. Рекурсивный способ состоит в задании функции через саму себя, при этом значения функции определяются через другие ее же значения. Такой способ задания функции используется в задании множеств и рядов.
При разложении числа Эйлера задается функцией:
Ее сокращение приведено ниже:
При прямом расчёте возникает бесконечная рекурсия, но можно доказать, что значение f(n) при возрастании n стремится к единице (поэтому, несмотря на бесконечность ряда, значение числа Эйлера конечно). Для приближённого вычисления значения e достаточно искусственно ограничить глубину рекурсии некоторым наперёд заданным числом и по достижении его использовать вместо f(n) единицу.
Источник
Проверка результатов и выставление оценки в контрольной работе 1
После того как студенты завершили выполнение контрольной работы 1, необходимо провести проверку результатов и выставить оценки. Это позволит объективно оценить знания студентов и определить их успеваемость в данном предмете.
Первым шагом при проверке результатов является анализ выполненных заданий. Возможно, что студенты допустили опечатки или ошибки при составлении ответов
Поэтому важно внимательно просмотреть все задания и проверить правильность ответов
Для проведения проверки можно использовать различные подходы. Например, можно создать таблицу, в которой будут указаны все задания и правильные ответы. Затем, просматривая работы студентов, можно сравнивать их ответы с правильными и отмечать количество правильных и неправильных ответов.
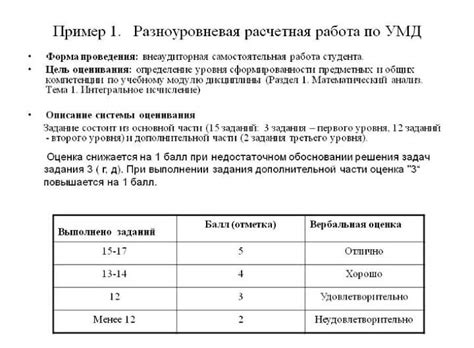
После проведения проверки можно приступить к выставлению оценок. Чаще всего для этого используется шкала оценок от 2 до 5. Оценка 2 ставится за неудовлетворительные результаты, оценка 3 — за удовлетворительные, оценка 4 — за хорошие, а оценка 5 — за отличные результаты.
При выставлении оценок необходимо учитывать не только количество правильных ответов, но и качество выполнения работы, эрудицию студентов и умение применять полученные знания на практике
Поэтому рекомендуется проводить детальный анализ работ и принимать во внимание все аспекты выполнения заданий
Важно помнить, что цель контрольной работы — не только проверить знания студентов, но и помочь им закрепить материал и понять слабые места. Поэтому после выставления оценок рекомендуется провести обсуждение результатов и объяснить студентам, в чем заключаются их ошибки и как их можно исправить
Таким образом, проверка результатов и выставление оценки в контрольной работе 1 является важным этапом в образовательном процессе. Она позволяет оценить знания студентов, помочь им улучшить свои навыки и достичь лучших результатов.
Построение графика функции
Одну и ту же зависимость возможно порою задать как аналитически, так и графически. Графики помогают при решении многих сложных задач, ведь они наглядно иллюстрируют поведение функций. Посмотрим, как построить график функции, если для нее известна формула, ее описывающая.
Пусть дана зависимость
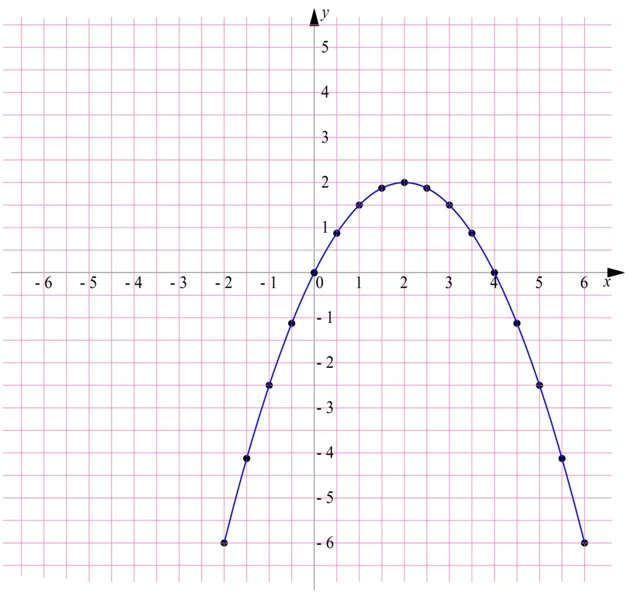
y(x) = 0.5x(4 — x)
Будем строить для нее график при значениях x от – 2 до 6. Для этого запишем в таблице все возможные целые значения х и вычислим для них величину y.Покажем несколько примеров расчета:
y(-2) = 0.5*(-2)(4-(-2)) = -6
y(-1) = 0.5*(-1)(4-(-1)) = -2.5
y(0) = 0.5*0*(4-0) = 0
Таким образом заполняется вся таблица:

Получили координаты 9 точек, которые отметим на плоскости (для первых двух точек пунктирами показано, как нашли их местоположение):
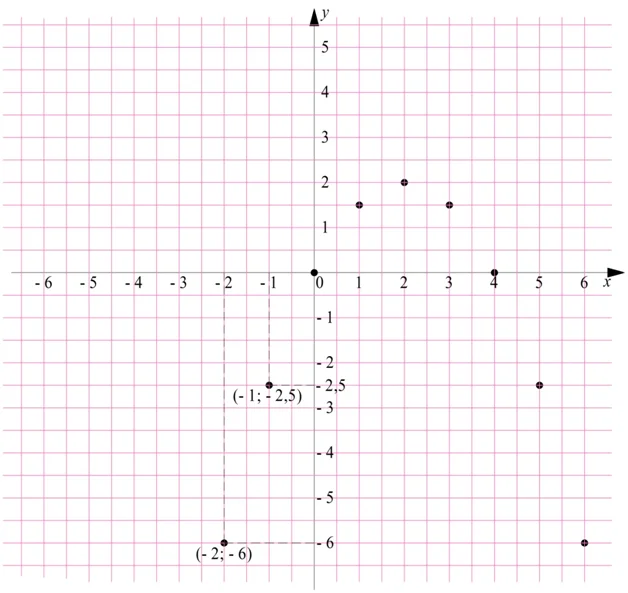
Они уже «намечают» некоторую линию. Конечно, отметить все возможные точки невозможно. Однако при необходимости можно «уплотнить» точки на графике, вычислив у ещё при некоторых дробных значениях x, например:
y(-1.5) = 0.5*(-1.5)(4-(-1.5)) = 4.125
y(-0.5) = 0.5*(-0.5)(4-(-0.5)) = 1.125
Отложим эти и ещё несколько дополнительных точек на графике:
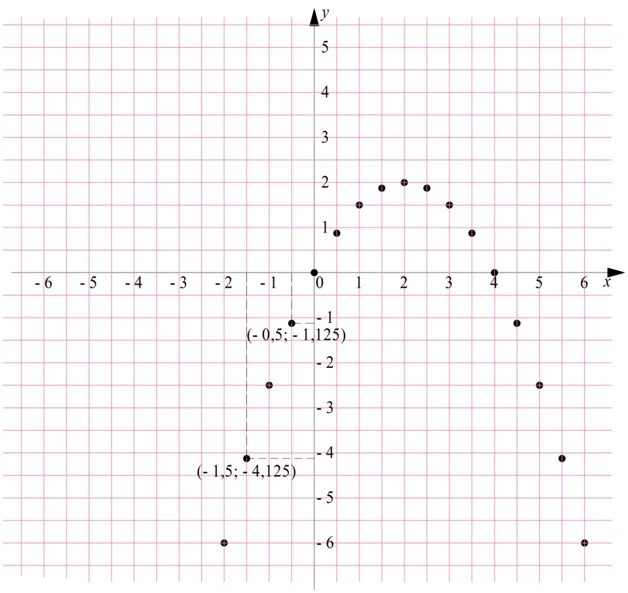
С помощью современной компьютерной техники можно почти мгновенно вычислить местоположение миллионов таких точек. Соединив их все плавной линией, получим график:
Домен и диапазон функций
Функции являются фундаментальной концепцией в математике, и они широко используются во многих областях, таких как экономика, физика, инженерия и информатика.Они помогают представлять и анализировать отношения между переменными.Одним из основных аспектов функции является его домен и диапазон.Домен представляет собой набор всех входных значений (также известных как независимые переменные), который может использоваться в качестве входной функции для функции.С другой стороны, диапазон представляет собой набор всех выходных значений (также известных как зависимые переменные), которые создаются при использовании этих входных значений.
1. Домен функции можно определить, рассматривая входные значения, которые разрешены для использования в функции.Например, если у нас есть функция, которая представляет область квадрата, то домен этой функции-все это нетрицательные реальные числа.Мы не можем использовать отрицательные числа или сложные числа, так как эти значения не имеют смысла, когда мы имеем дело с площадью квадрата.
2. Диапазон функции можно определить путем изучения выходных значений, которые создаются при использовании входных значений.Например, если у нас есть функция, которая представляет высоту мяча после того, как он был брошен, то диапазон этой функции-все это неотрицательные реальные числа.Мы не можем иметь отрицательные значения, так как высота мяча не может быть отрицательной.
3. Возможно иметь функции, в которых домен и диапазон не являются всеми возможными значениями.Например, если у нас есть функция, которая представляет температуру воды на разных высотах, то домен этой функции-все это неотрицательные реальные числа, но диапазон ограничен определенным диапазоном температур.
4. В некоторых случаях мы можем ограничить домен функции для получения новой функции.Например, если у нас есть функция, которая представляет площадь квадрата, мы можем ограничить домен только положительными целыми числами, чтобы получить новую функцию, которая представляет область квадрата с длиной боковой, которая является положительным целым числом.
Понимание домена и диапазона функции имеет решающее значение при работе с функциями.Это помогает нам понять поведение функции и ее ограничения.Зная область и диапазон, мы можем определить, является ли функция хорошо определенной или нет, и мы можем избежать ошибок при работе с функциями.
Домен и диапазон функций — Функции: применение алгебраического метода для анализа функций
Степенная функция с натуральным показателем
Если обозначить сторону квадрата как a, то его площадь будет являться функцией:
S = a2
Для вычисления объема куба с ребром a необходимо возводить число уже в третью степень:
V = a3
Эти выражения являются примерами степенных функций с натуральным показателем. Таковой будет являться любое уравнение y = xs, где s – это какое-то натуральное число.

При s = 1 степенная функция обращается в зависимость у = х, то есть в прямую пропорциональность. Независимая величина х может принимать любые значения, а вот область значений зависит от четности или нечетности показателя s (этот вопрос будет рассмотрен подробнее чуть позже).
Рассмотрим функцию y = x2. Ясно, что при х, равном нулю, зависимая переменная также обращается в нуль:
y(0) = 02 = 0
Следовательно, ее график проходит через точку О (0;0). Это характерное свойство степенных функций с любым натуральным показателем.
Квадрат любого числа не может быть отрицательным числом, а потому график лежит в I и II четвертях. Следовательно, областью значений будет являться всё множество неотрицательных действительных чисел.
Заметим, что противоположным значениям х соответствуют одинаковые значения y:
y(-x) = (-x)2 = x2 = y(x)
Из-за этого график обладает симметрией относительно оси у.
Найдем несколько точек, по которым можно построить график степенной функции:

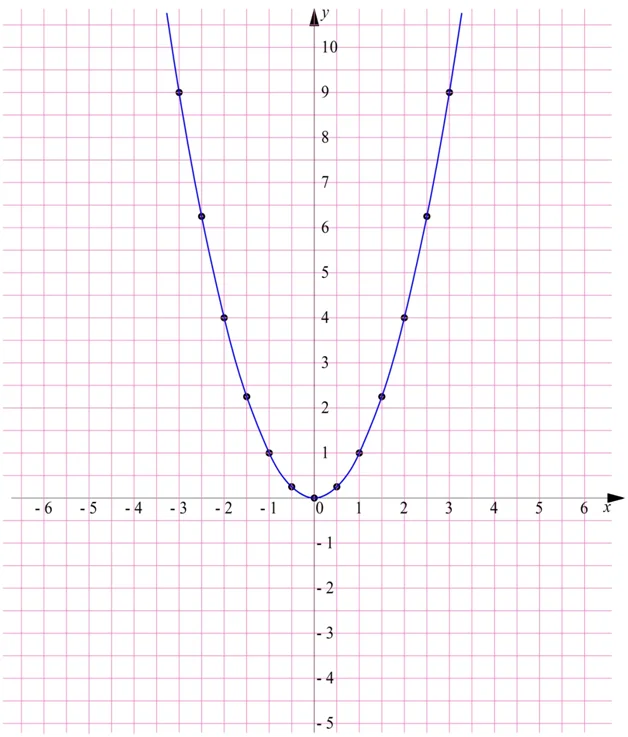
Полученную фигуру называют параболой, а точку О (0;0) – вершиной параболы. Видно, что точки параболы располагаются симметрично относительно оси ординат.
Заметим, что у степенных функций с четным показателем графики похожи. Они все симметричны относительно оси у, а также у них есть три общие точки:
- (0;0);
- (1;1);
- (– 1;1).
Они определены на множестве всех неотрицательных чисел. Чем выше показатель степени, тем более плотно график «прижимается» к горизонтальной оси при малых х и тем более резко он поднимается вверх при больших х:
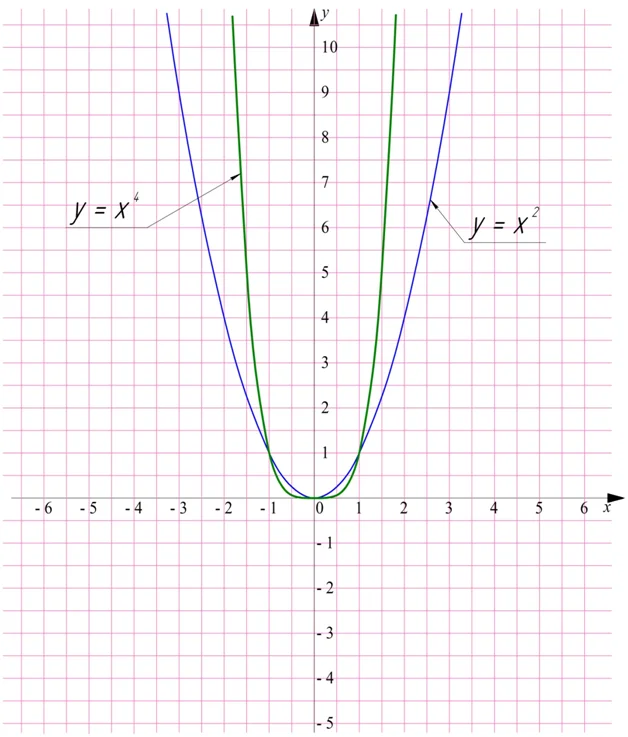
Далее изучим те степенные функции, показатель которых – нечетное число. Одной из них является
y = x3
Её график также пересекает начало координат. При положительном значении аргумента куб числа также положителен, а при отрицательном значении аргумента он будет отрицательным числом. Следовательно, график должен проходить через I и III четверти. Построим график по точкам:

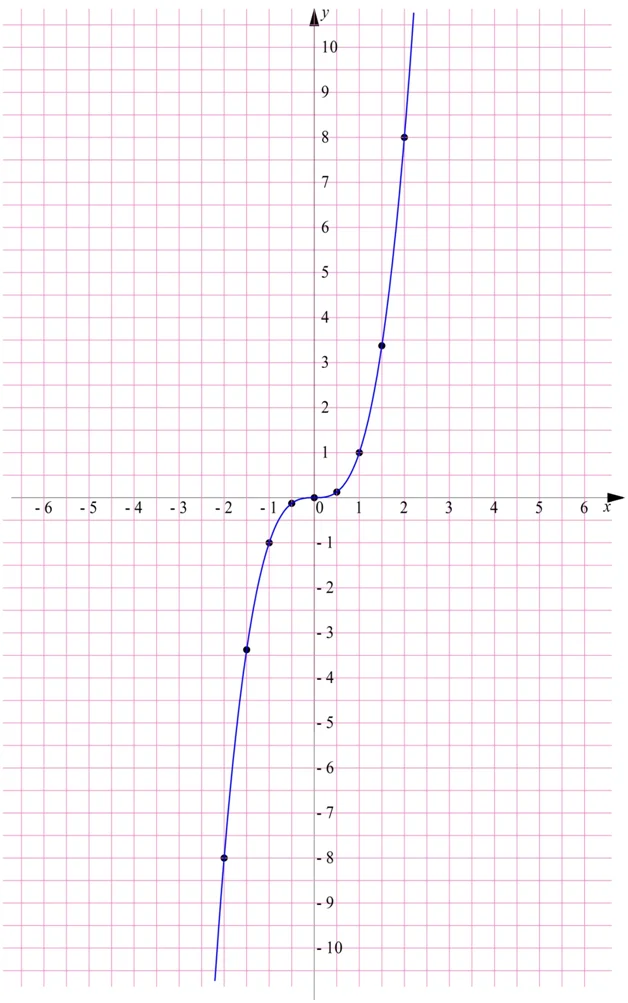
Полученный график называют кубической параболой. Графики других степенных функций (x5, x7, x9 и т.д.) похожи на этот:
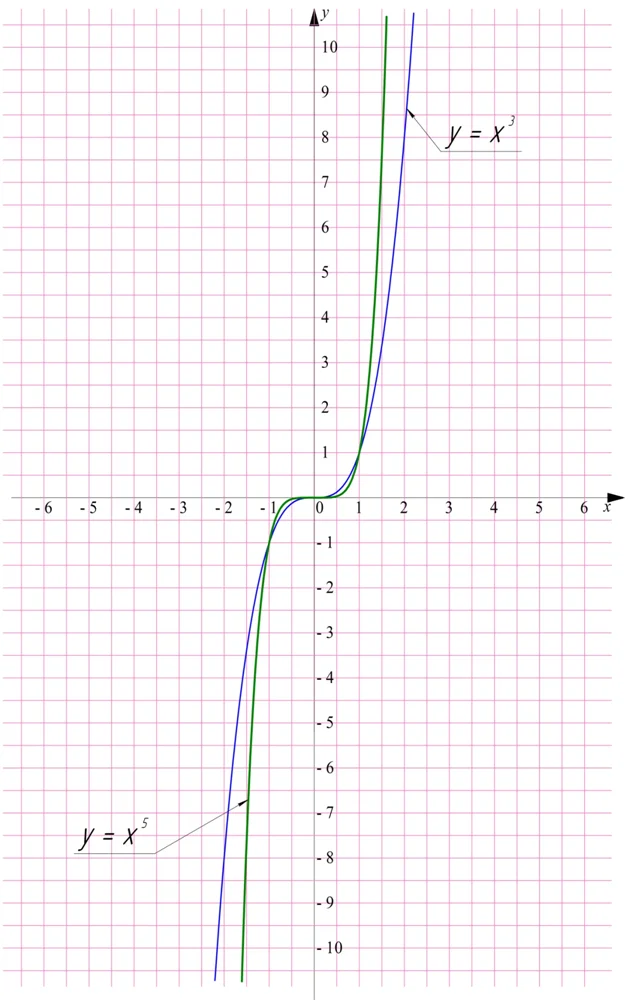
Они проходят через точки (0;0), (1;1) и (– 1; –1), лежат в I и III четвертях. У всех этих функций и в область значений, и область определений попадают все действительные числа.
Решение уравнений с участием функций
При работе с функциями одним важным аспектом является способность решать уравнения, которые их вовлекают.Этот процесс похож на решение других типов уравнений, но он требует дополнительного шага понимания того, как ведут себя функции.По сути, нам необходимо применить алгебраические методы для анализа функций, что может дать ценную информацию об их свойствах.С практической точки зрения, это может помочь нам понять, как функции ведут себя в реальных ситуациях, где их можно использовать для моделирования сложных систем.Например, если мы имеем дело с системой, которая включает в себя функцию, мы можем использовать алгебраические методы для решения уравнений и делать прогнозы о его поведении.
Вот несколько ключевых моментов, которые следует иметь в виду при решении уравнений с участием функций:
1. Понять свойства функции: прежде чем мы сможем решить уравнение с участием функции, нам нужно понять, как оно ведет себя.Это включает в себя понимание его домена и диапазона, будь то непрерывное или прерывистое, и будь то один на один или многие к одному.Понимая эти свойства, мы можем принимать обоснованные решения о том, как приблизиться к уравнению.
2. Примените алгебраические методы: как только мы поймем функцию, мы можем применить алгебраические методы для решения уравнения.Это может включать упрощение уравнения, факторинг, с использованием квадратичной формулы или других алгебраических методов.Цель состоит в том, чтобы изолировать переменную (обычно представленную X) на одной стороне уравнения.
3
Проверьте на наличие посторонних решений: при решении уравнений, участвующих в функциях, важно проверить на наличие посторонних решений.Это может произойти, когда мы делаем предположения о функции, которая недопустима.Например, если мы предположим, что функция является один-к-одному, когда она на самом деле много-к-одному, мы можем в конечном итоге получить решения, которые не работают
4. Используйте технологию при необходимости: в некоторых случаях может быть трудно или невозможно решить уравнение с участием функции с использованием только алгебраических методов.В этих случаях может потребоваться использовать такие технологии, как график калькуляторов или компьютерное программное обеспечение для поиска решений.
В целом, решение уравнений, включающих функции, является важным навыком для тех, кто работает с функциями.Понимая свойства функции, применяя алгебраические методы, проверяя посторонние решения и использование технологии при необходимости, мы можем получить ценную информацию о том, как ведут себя функции и как их можно использовать для моделирования реальных систем.
Решение уравнений с участием функций — Функции: применение алгебраического метода для анализа функций
Графическое задание функции
article>ÐÑедÑÑавÑÑе, ÑÑо Ð´Ð»Ñ ÑколÑной наÑÑной конÑеÑенÑии Ð²Ñ Ð³Ð¾ÑовиÑе доклад о загÑÑзнении окÑÑжаÑÑей ÑÑедÑ. Ðак вÑ
дÑмаеÑе, ÑÑо пÑоизведÑÑ Ð±Ð¾Ð»ÑÑий ÑÑÑÐµÐºÑ Ð½Ð° аÑдиÑоÑиÑ:
-
пеÑеÑиÑление ÑÑаÑиÑÑиÑеÑÐºÐ¸Ñ Ð´Ð°Ð½Ð½ÑÑ Ð¾Ð± ÑвелиÑении колиÑеÑÑва мÑÑоÑа за поÑледний год;
-
наглÑÐ´Ð½Ð°Ñ Ð´ÐµÐ¼Ð¾Ð½ÑÑÑаÑÐ¸Ñ ÑоÑÑа загÑÑзнений в виде гÑаÑика?
ÐеÑно â иллÑÑÑÑаÑии, ÑоÑогÑаÑии, гÑаÑики и диагÑÐ°Ð¼Ð¼Ñ Ð³Ð¾Ð²Ð¾ÑÑÑ Ð¿Ð¾Ñой гÑомÑе лÑбÑÑ Ñлов!
ÐÐ»Ñ Ð½Ð°Ð³Ð»Ñдного оÑобÑÐ°Ð¶ÐµÐ½Ð¸Ñ Ð·Ð°Ð²Ð¸ÑимоÑÑи одной пеÑеменной Ð¾Ñ Ð´ÑÑгой Ð¼Ñ Ð²Ð²ÐµÐ´Ñм ÑиÑÑÐµÐ¼Ñ ÐºÐ¾Ð¾ÑдинаÑ, в коÑоÑой поÑÑÑоим гÑаÑик.
ÐÑаÑик â ÑÑо пÑÑмаÑ, кÑÐ¸Ð²Ð°Ñ Ð¸Ð»Ð¸ Ð»Ð¾Ð¼Ð°Ð½Ð°Ñ Ð»Ð¸Ð½Ð¸Ñ, коÑоÑÐ°Ñ Ð±Ñла поÑÑÑоена ÑÑÑко по ÑÑавнениÑ
(ÑÑнкÑии).
Ðак Ð¼Ñ Ñже говоÑили, ÑÑнкÑÐ¸Ñ ÑоÑÑÐ¾Ð¸Ñ Ð¸Ð· завиÑимой и незавиÑимой пеÑеменной. РдекаÑÑовой ÑиÑÑеме кооÑдинаÑ
незавиÑÐ¸Ð¼Ð°Ñ Ð¿ÐµÑÐµÐ¼ÐµÐ½Ð½Ð°Ñ Ð¾ÑобÑажаеÑÑÑ Ñ Ð¿Ð¾Ð¼Ð¾ÑÑÑ Ð¾Ñи
завиÑÐ¸Ð¼Ð°Ñ â Ñ Ð¿Ð¾Ð¼Ð¾ÑÑÑ Ð¾Ñи
РзавиÑимоÑÑи Ð¾Ñ Ñипа ÑÑнкÑии гÑаÑик Ð¼Ð¾Ð¶ÐµÑ Ð²ÑглÑдеÑÑ, напÑимеÑ, Ñак:

Определение основных показателей

В контексте заданного правила, основные показатели могут быть определены для измерения эффективности или успешности функции. Они могут использоваться для оценки достижения целей и определения прогресса. Ниже приведены некоторые из основных показателей, которые могут быть использованы:
| Показатель | Описание |
|---|---|
| Выполнение | Показывает, насколько функция была выполнена в соответствии с требованиями и ожиданиями. |
| Качество | Определяет соответствие функции установленным стандартам и требованиям к качеству. |
| Время | Оценивает время, необходимое для выполнения функции и достижения результата. |
| Затраты | Определяет материальные и финансовые затраты, связанные с выполнением функции. |
| Удовлетворенность клиентов | Оценивает степень удовлетворенности клиентов результатами функции. |
Эти показатели могут быть измерены и отслеживаемы в процессе выполнения функции и могут быть использованы для улучшения ее результатов и эффективности.
Способы задания функции
Самый простой способ задания какой-либо зависимости – описательный, или словесный. Вот пример такого описания: «каждому нечетному числу x соответствует число y, равное его наименьшему делителю (не считая единицы)». Такая формулировка значит, что, например, числу 15 соответствует число 3, ведь 15 делится только на 3 и 5, а тройка меньше пятерки. Числу 91 соответствует 7, так как 91 делится на 7 и 13. А какое число соответствует, скажем, 12? Никакое, ведь в описании функции указано, что аргументом должно быть нечетное число, а 12 – четное.
Чаще всего в алгебре применяют аналитический способ задания функции. Он подразумевает, что записывается формула, позволяющая по значению независимой величины вычислить величину зависимую:
Этим записям аналогична другая, где аргумент прямо указывается в скобках после зависимой величины:
Иногда функция может быть представлена в виде алгоритма. Например: «для вычисления значения g(х) необходимо сложить все десятичные цифры, из которых состоит натуральное число x». Тогда для аргумента 135 функция будет равна 9:
g(135) = 1 + 3 + 5 = 9
Вот ещё несколько значений этой функции:
g(89) = 8 + 9 =17
g(5656) = 5 + 6 + 5 +6 = 22
Подобный подход нередко встречается в некоторых языках программирования.
Если область определения функции не содержит бесконечное число чисел, то ее можно задать таблицей.В ней указывают все возможные значения независимой величины, а также соответствующие её значения зависимой величины. Вот пример табличной функции, задающей соответствие между размерами европейскими и английскими размерами мужских пальто:

А вот ещё одна табличная функция, которая каждому натуральному числу n от 1 до 5 ставит в соответствие число, равное 2n + 3:
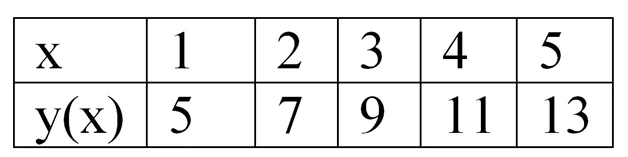
По приведенной таблице легко определить, что
y(1) = 5
y(2) = 7
y(3) = 9
y(4) = 11
y(5) = 13
Очень распространен графический способ задания функции. Он предполагает, что нарисован график (линия или набор линий на координатной плоскости), с помощью которого можно по аргументу определить зависимую величину. Этот график может выглядеть так:
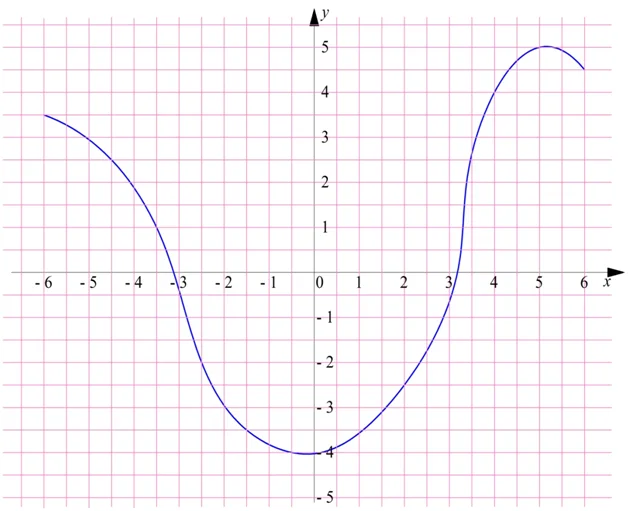
На координатной плоскости показана горизонтальная ось, по которой откладывают значение независимой переменной (в этом примере это х), и вертикальная ось, где отмечают зависимую переменную (у). Сам график показан синей линией. Покажем, как с его помощью находить значение y. Пусть надо узнать y(2), то есть значение y при x = 2. Находим на горизонтальной оси x (ее ещё называют осью абсцисс) число 2 и проводим с нее вертикальную линию до пересечения графика:
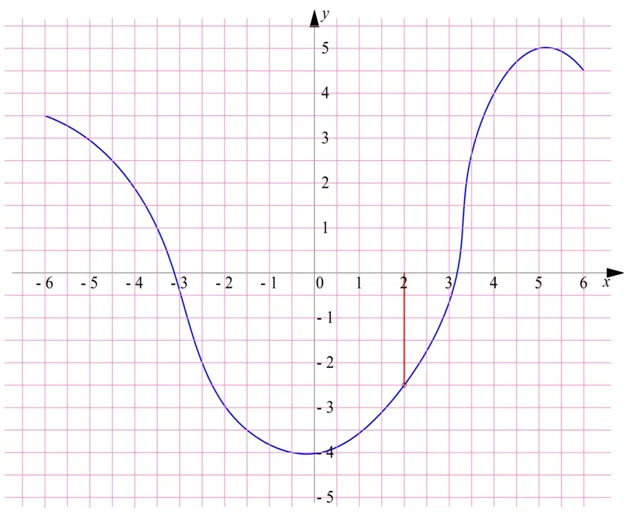
После этого от полученной точки проводится уже горизонтальная линия до пересечения с вертикальной осью y (другое ее название – ось ординат):
Далее смотрим, где именно горизонтальная линия пересекла ось у. В рассматриваемом случае получили, что у(2) = – 2,5.
Можно сформулировать определение графика функции:

Надо понимать, что не любая линия задает какую-нибудь функцию. Дело в том, что ни одна вертикальная линия не должна пересекаться с графиком в 2 и более точках, ведь тогда одному значению аргумента будет соответствовать несколько значений функции.Такая ситуация показана на рисунке:
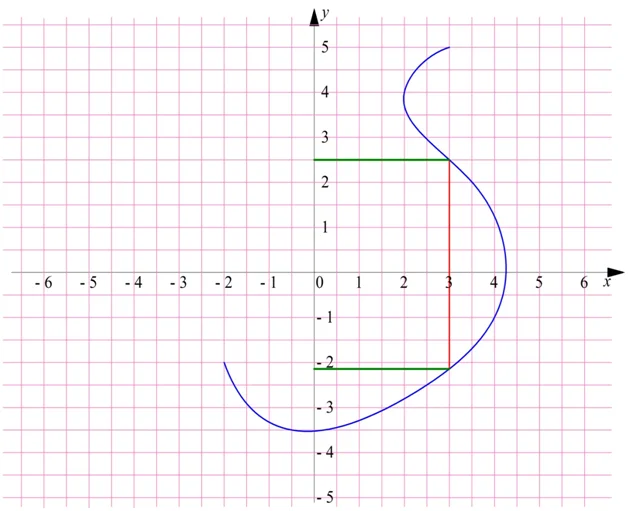
Здесь можно видеть, что для x = 3 можно указать два значения для y. Однако по определению значению независимой величины в соответствие ставится лишь одно значение зависимой переменной. Поэтому синяя линия здесь не является графиком функции (приведен как пример того, что не всякая линия может являться графиком функции). Нередко полностью построить график невозможно. Например, зависимость
y = x + 2
определена и при x = 1, и при x =1000000000000000000. Поэтому иногда график строят частично, чтобы наглядно были видны его особенности.
Примерами графических функций являются кардиограммы, фиксирующие работу сердца, а также показания сейсмографа – прибора, измеряющего силу землетрясений.
Что делают условные операторы в Python
Условные операторы в Python используют для разработки программ, которые учитывают разные условия и на их основе выполняют определённые действия. Чаще всего их используют для следующих задач:
- Принятие решений. Позволяют программе выбирать между различными путями выполнения. Например, отправить пользователю письмо на почту или сообщение в мессенджере.
- Контроль потока выполнения. Условные операторы управляют тем, какие части кода будут выполнены, а какие проигнорированы.
- Оптимизация кода. Позволяют избегать выполнения ненужных операций, что улучшает производительность. Действия в программе выполняются последовательно, но иногда некоторые операции надо пропустить.
- Обработка ошибок. Условные операторы помогают обнаруживать и реагировать на ошибки или нестандартные ситуации. С помощью условных операторов можно описать, как программе реагировать на возникающие в коде ошибки.
Наименьшее и наибольшее значение функции на открытом или бесконечном интервале
В чём отличие отрезка от интервала? В отрезке определены крайние точки, в интервале же крайние точки могут не
существовать (например ), или значение функции в них мы рассматривать не будем (на интервале
мы рассмотрим значение функции в окрестностях этих точек, но не в них самих).
Вариантов задания интервала может быть множество, но каждый из них сведёт определение
и к поиску производной и вычислению пределов в крайних точках, например
и
Вернёмся на пару шагов назад. А что такое предел функции?
Если говорить коротко, то предел функции — это такое число , к которому функция стремится, в то время как аргумент стремится достичь числа
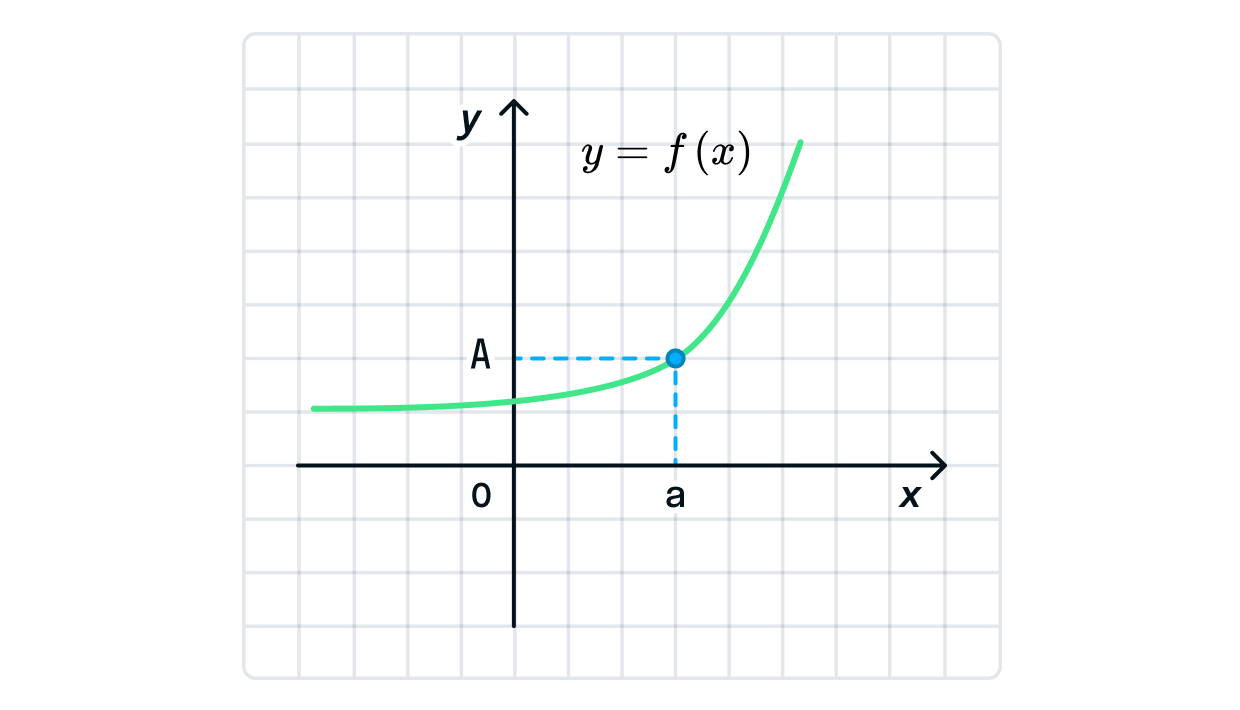
Предположим, наша функция представлена уравнением Найдём предел функции при подставив это значение вместо в уравнение:
Это означает, что функция стремится приблизиться к числу в то время как аргумент тоже приближается к этому значению. В отрыве от настоящего
уравнения мы могли бы представить это так:
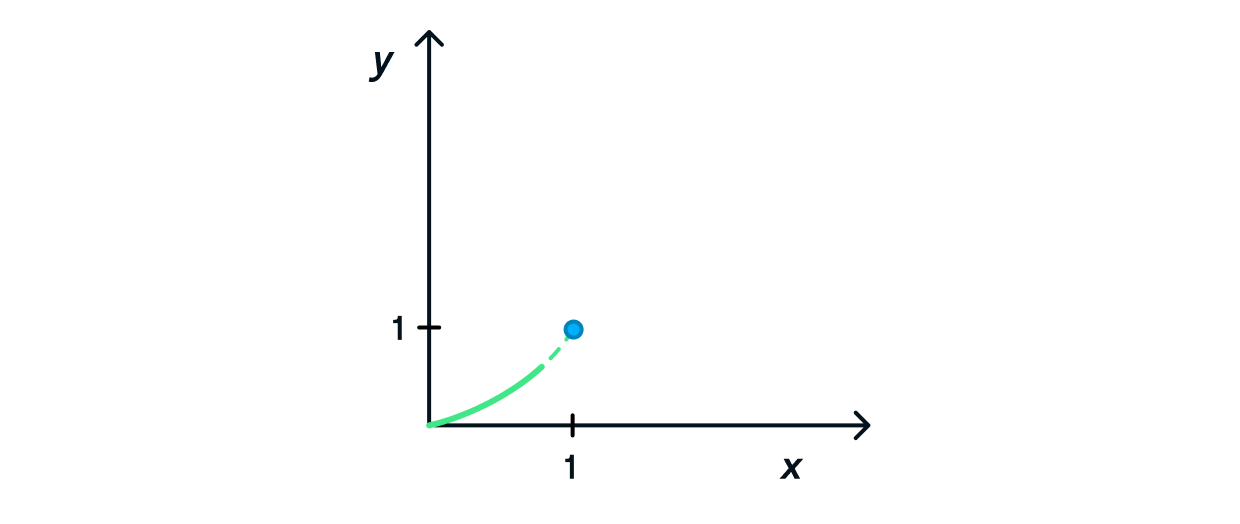
Функция может стремиться не только к рациональному
числу, но также и к бесконечности. В таком случае при подстановке бесконечности в функцию возникает
неопределённость, которую необходимо решить разными методами.
В рамках этой статьи мы не можем посвятить этому много времени, поэтому ждём Вас на курсах математики в онлайн-школе
Skysmart — там ни один предел не останется незамеченным.
Вернёмся к функции! Итак, как же определить наибольшее и наименьшее значение на интервале?
-
Найдём область определения данной функции и проверим, входит ли в неё заданный интервал.
-
Найдём производную данной функции.
-
Приравняем производную к нулю и найдём точки, в которых она обращается в нуль (решим уравнение).
-
Выберем из корней уравнения те точки, которые попадают в заданный промежуток, и вычислим значение функции в
них. -
Возьмём крайние точки интервала и вычислим значение предела в этих точках (согласно типу интервала).
-
Сделаем вывод о наибольшем и наименьшем значении функции.
Для вычисления предела вам поможет сводная таблица, которая учитывает вид интервала:
|
Интервал |
Предел |
|---|---|
| и | |
|
и |
|
|
и |
Если при вычислении одностороннего предела вы получаете бесконечность, то вычислить наибольшее/наименьшее
значение невозможно.

Задача 3
Необходимо найти наибольшее и наименьшее значение функции на всём промежутке области определения.
Решение:
-
ОДЗ:
-
Найдём стационарные точки:
-
Точка
входит в промежуток области определения и является точкой минимума. -
Так как
— парабола, ветви которой направлены вверх, мы не можем определить точку
максимума.
Cегодня мы на славу потрудились и разобрали множество важных вопросов:
-
что такое функция, какой она бывает;
-
что такое наименьшее и наибольшее значение функции;
-
как определить и на отрезке;
-
как находить наименьшее и наибольшее значение функции на интервале;
-
что такое предел и производная.




























