Расчет натяжения троса и реакции опоры
Задача
Однородная балка AB весом P закреплена в точке A шарнирно-неподвижной опорой; трос BC, удерживающий балку, составляет с ней угол α. Определить натяжение троса и реакцию опоры A (рисунок 2.2, а).
Решение
Силы, действующие на балку, приложены к разным ее точкам, поэтому в данной задаче нужно рассмотреть равновесие балки. Балка однородная, поэтому сила P (вес балки) приложена к ее середине (рисунок 2.2, б).
Реакция троса – сила T – направлена вдоль троса. Направление реакции опоры A можно определить, воспользовавшись теоремой о трех силах. По этой теореме линии действия трех непараллельных сил P, T и RA должны пересекаться в одной точке. То есть угол β должен быть равен углу α.

Рисунок 2.2
Так как система находится в равновесии, то
P + T + RA=0. (2.7)
Строим это геометрическое равенство (рисунок 2.3), начиная с известной силы P; под углом α к горизонтали через конец векторa P проводим линию MN, вдоль которой направлена сила T. Так как сумма всех сил должна быть равна нулю, то вектор RA должен заканчиваться в начале вектора P под углом β к горизонту (линия KL).
Рисунок 2.3
Точка пересечения линий MN и KL – это конец вектора T и начало вектора RA. Далее можно определить величины T и RA, умножив длины отрезков на выбранный масштаб или воспользовавшись теоремой синусов:

Аналитическое решение предполагает составление двух уравнений. Проецируем векторное равенство (2.7) на выбранные оси координат (рисунок 2.2,б) и получаем два уравнения равновесия с двумя неизвестными:
∑xi=0, -Tcosα+RAcosβ=0;∑yi=0, -P+Tsinα+RAsinβ. (2.10)
Из этих уравнений определяются величины T и RA:
Другие примеры решения задач >>
isopromat.ru
Виды простейших механизмов, что считается идеальным механизмом
Сегодня выделяют восемь простейших механизмов, среди которых некоторые являются разновидностями основных.
- Наклонная плоскость. Представляет собой плоскость, расположение которой находится под острым углом к обычной горизонтальной поверхности. Используется в клине (за счет нее увеличивается давление на небольшой плоскости). Примеры: лопата, пуля, копье и т.п. Второй пример — винт. Механизм его действия используется в дрелях, шуруповертах, для подъема воды (Архимедов винт) и т.п.
- Рычаг. Задачей, определяющей применение, является подъем тяжести. Кроме того, он необходим, как выключатель и спусковой крючок, например, в ткацком станке, паровой машине и т.п. Основными представителями являются:
- ворот (задействован при подъеме воды в колодце, в ременной передаче и т.п.);
- блок (выглядит как колесо, имеющее желоб. По желобу располагается веревка, трос, цепь и т.п).
- Колесо. Основная часть в устройстве транспорта, для зубчатых передач.
- Поршень. Краткая характеристика сводится к использованию энергии нагретого газа, который в расширенном состоянии совершает работу. Примеры: двигатель внутреннего сгорания, огнестрельное оружие, паровая машина.
Принципы их действия описаны в следующем разделе.
Для того чтобы простейший механизм являлся идеальным, он не должен рассеивать энергию на погашение собственной силы трения, износ либо деформацию. Энергия должна полностью расходоваться на выходную мощность. Тогда механический выигрыш будет равен геометрическим расчетам.
Несмотря на то, что принцип работы каждой машины своеобразен, ожидаемый результат всегда направлен на изменение силы, необходимой для выполнения работы по перемещению груза.
Для простейших механизмов характерно отсутствие источника энергии. Поэтому для них нереально выполнение работ без получения входящей силы. А, благодаря тому, что в идеальном механизме эта поступающая сила не расходуется на компенсацию побочных воздействий (сила трения и т.д.), происходит сохранение механической энергии. Следовательно, потребляемая мощность равна выходной работе.
2.3. Свободные колебания. Математический маятник window.top.document.title = «2.3. Свободные колебания. Математический маятник»;
Математическим маятником называют тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. В положении равновесия, когда маятник висит по отвесу, сила тяжести уравновешивается силой натяжения нити При отклонении маятника из положения равновесия на некоторый угол φ появляется касательная составляющая силы тяжести Fτ = –mg sin φ (рис. 2.3.1). Знак «минус» в этой формуле означает, что касательная составляющая направлена в сторону, противоположную отклонению маятника.
| Рисунок 2.3.1.Математический маятник. φ – угловое отклонение маятника от положения равновесия, x = lφ – смещение маятника по дуге |
Если обозначить через x линейное смещение маятника от положения равновесия по дуге окружности радиуса l, то его угловое смещение будет равно φ = x / l. Второй закон Ньютона, записанный для проекций векторов ускорения и силы на направление касательной, дает:
Это соотношение показывает, что математический маятник представляет собой сложную нелинейную систему, так как сила, стремящаяся вернуть маятник в положение равновесия, пропорциональна не смещению x, а
Только в случае малых колебаний, когда приближенно можно заменить на математический маятник является гармоническим осциллятором, т. е. системой, способной совершать гармонические колебания. Практически такое приближение справедливо для углов порядка 15–20°; при этом величина отличается от не более чем на 2 %. Колебания маятника при больших амплитудах не являются гармоническими.
Для малых колебаний математического маятника второй закон Ньютона записывается в виде
Таким образом, тангенциальное ускорение aτ маятника пропорционально его смещению x, взятому с обратным знаком. Это как раз то условие, при котором система является гармоническим осциллятором. По общему правилу для всех систем, способных совершать свободные гармонические колебания, модуль коэффициента пропорциональности между ускорением и смещением из положения равновесия равен квадрату круговой частоты:
Эта формула выражает собственную частоту малых колебаний математического маятника.
Следовательно,
 |
|
Модель. Математический маятник |
Любое тело, насаженное на горизонтальную ось вращения, способно совершать в поле тяготения свободные колебания и, следовательно, также является маятником. Такой маятник принято называть физическим (рис. 2.3.2). Он отличается от математического только распределением масс. В положении устойчивого равновесия центр масс C физического маятника находится ниже оси вращения О на вертикали, проходящей через ось. При отклонении маятника на угол φ возникает момент силы тяжести, стремящийся возвратить маятник в положение равновесия:
Здесь d – расстояние между осью вращения и центром масс C.
| Рисунок 2.3.2.Физический маятник |
Знак «минус» в этой формуле, как обычно, означает, что момент сил стремится повернуть маятник в направлении, противоположном его отклонению из положения равновесия. Как и в случае математического маятника, возвращающий момент M пропорционален sin φ. Это означает, что только при малых углах φ, когда sin φ ≈ φ, физический маятник способен совершать свободные гармонические колебания. В случае малых колебаний
см. §1.23
εIO
Здесь ω – собственная частота малых колебаний физического маятника.
Следовательно,
Более строгий вывод формул для ω и T можно сделать, если принять во внимание математическую связь между угловым ускорением и угловым смещением: угловое ускорение ε есть вторая производная углового смещения φ по времени:
Поэтому уравнение, выражающее второй закон Ньютона для физического маятника, можно записать в виде
Это уравнение свободных гармонических колебаний (). Коэффициент в этом уравнении имеет смысл квадрата круговой частоты свободных гармонических колебаний физического маятника.
По теореме о параллельном переносе оси вращения (теорема Штейнера) момент инерции I можно выразить через момент инерции IC относительно оси, проходящей через центр масс C маятника и параллельной оси вращения:
Окончательно для круговой частоты ω свободных колебаний физического маятника получается выражение:
| клеймо для выжигания по дереву |
| znakmastera.ru |
Работа равнодействующей силы, тяжести, трения, упругости. Мощность, коэффициент полезного действия. Примеры, формулы
Работа
Работа — это скалярная величина, которая определяется по формуле

Работу выполняет не тело, а сила! Под действием этой силы тело совершает перемещение.
Обратите внимание, что у работы и энергии одинаковые единицы измерения. Это означает, что работа может переходить в энергию
Например, для того, чтобы тело поднять на некоторую высоту, тогда оно будет обладать потенциальной энергией, необходима сила, которая совершит эту работу. Работа силы по поднятию перейдет в потенциальную энергию.
Правило определения работы по графику зависимости F(r): работа численно равна площади фигуры под графиком зависимости силы от перемещения.
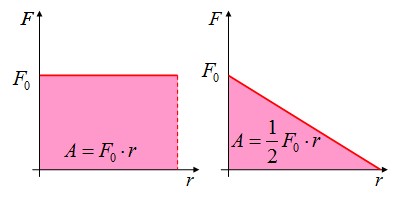
Угол между вектором силы и перемещением
1) Верно определяем направление силы, которая выполняет работу; 2) Изображаем вектор перемещения; 3) Переносим вектора в одну точку, получаем искомый угол.
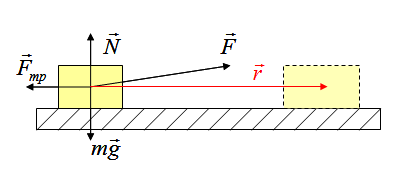
На рисунке на тело действуют сила тяжести (mg), реакция опоры (N), сила трения (Fтр) и сила натяжения веревки F, под воздействием которой тело совершает перемещение r.
Для нахождения работы, совершенной силой упругости, необходимо учесть, что эта сила изменяется, так как зависит от удлинения пружины. Из закона Гука следует, что при увеличении абсолютного удлинения, сила увеличивается.
Для расчета работы силы упругости при переходе пружины (тела) из недеформированного состояния в деформированное используют формулу
Мощность
Скалярная величина, которая характеризует быстроту выполнения работы (можно провести аналогию с ускорением, которое характеризует быстроту изменения скорости). Определяется по формуле
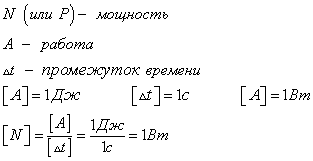
Коэффициент полезного действия
КПД — это отношение полезной работы, совершенной машиной, ко всей затраченной работе (подведенной энергии) за то же время
Коэффициент полезного действия выражается в процентах. Чем ближе это число к 100%, тем выше производительность машины. Не может быть КПД больше 100, так как невозможно выполнить больше работы, затратив меньше энергии.
КПД наклонной плоскости — это отношение работы силы тяжести, к затраченной работе по перемещению вдоль наклонной плоскости.
Главное запомнить
1) Формулы и единицы измерения;2) Работу выполняет сила; 3) Уметь определять угол между векторами силы и перемещения
Если работа силы при перемещении тела по замкнутому пути равна нулю, то такие силы называют консервативными или потенциальными. Работа силы трения при перемещении тела по замкнутому пути никогда не равна нулю. Сила трения в отличие от силы тяжести или силы упругости является неконсервативной или непотенциальной.
Есть условия, при которых нельзя использовать формулу Если сила является переменной, если траектория движения является кривой линией. В этом случае путь разбивается на малые участки, для которых эти условия выполняются, и подсчитать элементарные работы на каждом из этих участков. Полная работа в этом случае равна алгебраической сумме элементарных работ:
Значение работы некоторой силы зависит от выбора системы отсчета.
Значение невесомости и нерастяжимости нити в науке
Нить, обладающая свойствами невесомости и нерастяжимости, играет важную роль в многих научных областях. Её уникальные свойства стали основой для разработки и проведения различных экспериментов и исследований.
В физике, невесомая нить используется для создания моделей и демонстраций физических явлений. Например, она может быть использована для изучения механики системы под действием гравитационных сил или для создания маятников и колебательных систем. Невесомая нить позволяет исключить влияние силы тяжести и сосредоточиться исключительно на изучении других физических особенностей системы.
В микробиологии и биохимии невесомость и нерастяжимость нити играют важную роль при проведении опытов и анализе различных образцов. Она может использоваться для изоляции отдельных клеток или генов, для создания мембран и фильтров, для манипулирования жидкостями и реагентами. Нити с указанными свойствами позволяют контролировать и управлять микроскопическими объектами, что открывает широкие возможности для исследования и разработки новых методов и технологий.
Кроме того, невесомая и нерастяжимая нить нашла применение в аэронавтике и космических исследованиях. В условиях невесомости, она может использоваться для крепления и фиксации различных элементов и оборудования на борту космических аппаратов. Недеформируемость нити позволяет обеспечить надежность и стабильность фиксации, что является важным требованием при проведении экспериментов в космосе.
Итак, свойства невесомости и нерастяжимости нити не только удивительны с точки зрения физических законов, но и находят широкое применение в науке. Они позволяют расширить возможности исследования и анализа, а также разрабатывать новые методы и технологии, которые приводят к новым открытиям и достижениям в различных областях науки.
Что такое нерастяжимая нить в задачах по физике
Нерастяжимую нить можно представить как идеализированную веревку или иной объект, который не может быть растянут или сжат под воздействием силы. В реальности, все нити обладают некоторой степенью упругости и растягиваются до определенного предела. Однако, использование идеализированной нерастяжимой нити позволяет упростить анализ систем и получить более точные результаты.
Нерастяжимая нить является важным элементом в решении задач по физике, особенно в механике твердого тела и задачах о равновесии тел. Например, нерастяжимую нить часто используют для различных систем подвесов, условий равновесия и расчета сил.
| Примеры решения задач с нерастяжимой нитью |
|---|
1. Задача о подвешенном грузе:
|
2. Задача о ползущей машинке:
|
Использование нерастяжимой нити в решении физических задач позволяет упростить анализ систем и достичь более точных результатов. Вместе с тем, следует помнить, что нерастяжимая нить является идеализированной моделью и не учитывает эффекты, связанные с упругостью реальных материалов.
Простые механизмы — что это такое в физике
Порой физические действия требуют от человека огромных усилий. Над тем, как их облегчить, задумывались даже первобытные люди, используя палки-копалки, каменные топоры и другие орудия труда. Умение облегчить свой труд путем применения определенных технологий — главное отличие человека от животного. Проявление этого умения — изобретение простых механизмов, деятельность которых направлена на изменение направления силы.
В процессе действия простых механизмов происходит противодействие одной (приложенной для работы) силы против силы нагрузки
Если не принимать во внимание потерь на компенсацию силы трения, то работа, выполняемая над грузом, будет идентичной работе, которую выполняет приложенная сила. Уменьшить «выходную» силу можно за счет уменьшения расстояния, например, при перемещении груза
В физике даже существует термин «механический выигрыш». Он обозначает, во сколько раз выходная сила больше приложенной при использовании простого механизма.
Примерами «полезности» применения простых механизмов являются случаи, если нужно:
- Увеличить скорость перемещения груза (когда перемещаемую часть увязывают с длинным концом рычага).
- Применить простые «строительные блоки» в составе сложных машин, например, колеса, рычаги в конструкции велосипеда.
История появления первого простейшего механизма связана с именем Архимеда, которому принадлежит знаменитое изречение: «Дайте мне точку опоры, и я переверну Землю». Это выражение он сказал тогда, когда обнаружил механический выигрыш от применения такого приспособления как рычаг.
В последующем греческим философам принадлежит заслуга открытия пяти классических простых механизмов, с помощью которых можно компенсировать затраты энергии на приведение в движение грузов:
- рычаг;
- брашпиль;
- блок;
- клин;
- винт.
Однако в пору их открытий существовали теоретические ограничения использования статических простых механизмов. Другими словами, пока исключались динамические конструкции.
Действие простых механизмов, принцип работы рычага и блока, равенство сил на рычаге и блоке
Расстояние от неподвижной оси до концов рычага — l1 и l2.
В состоянии равновесия справедлива формула:
F1l1=F2l2
Из этого математического выражения следует соотношение:
F1÷F2=l1÷l2
Вывод: Коррекция прилагаемой силы будет во столько раз, во сколько раз одно плечо длиннее другого.
Именно таким образом работает правило рычага, которое работает при копании лопатой, разрезании ножницами. Такой же характер имеет механическая работа плоскогубцев.
В изображенном на рисунке неподвижном блоке ось вращения проходит перпендикулярно ему, через точку О.
Перекинутая нить имеет два конца, на один из которых подвешен груз весом Р. Из определения понятия «вес» следует, что вес – это та сила, с которой тело действует на опору (либо растягивает подвес). В рассматриваемой ситуации тело своим весом действует на точку D. Левый же конец свободен от груза. Чтобы привести блок в состояние равновесия, к левому концу нужно приложить силу F. Местом ее приложения является точка С.
Радиусом блока является расстояние между точками О и А. Именно этот отрезок представляет плечо силы F. Плечо веса Р равно отрезку ОВ, также равному радиусу блока. Таким образом, при использовании неподвижного блока рычаг имеет равную длину обоих плечей. Выигрыша относительно силы или расстояния нет: F=P. Когда груз вместе с нитью начнет движение, точка C переместится на такое же расстояние.
«Полезность» неподвижного блока заключается в том, что он позволяет корректировать направление прилагаемых усилий. Его механизм бывает часто представлен в структуре более сложных технических устройств.
Значение нерастяжимости нити в промышленности
Одной из основных причин, по которой нерастяжимость нити является такой востребованной характеристикой, является сохранение структуры и формы материала на протяжении всего процесса производства и использования. Если нить имеет возможность растягиваться, это может привести к искажению формы изделия, потере прочности и сохраняемым характеристикам. Нерастяжимость нити позволяет обеспечить стабильность и качество материала.
В текстильной промышленности нерастяжимость нити особенно важна при производстве тканей, швейных изделий и синтетических материалов. Она позволяет избежать деформаций и уплотнений в материале, обеспечивает точность размеров и снижает возможность повреждений при дальнейшей обработке.
В медицинской и спортивной промышленности нерастяжимая нить используется в создании швов и стежков, которые должны быть прочными и долговечными. Нерастяжимость нити обеспечивает сохранение шва и стежка в идеальном состоянии при любых нагрузках и растяжениях, что является особенно важным в контексте медицинских операций и спортивных тренировок.
В авиации и аэрокосмической промышленности нерастяжимость нити играет решающую роль в безопасности и надежности компонентов и конструкций. Она позволяет изготавливать сильные и стойкие соединения, которые способны выдерживать большие нагрузки и экстремальные условия, такие как высокие температуры и давления. Нити с высокой нерастяжимостью используются для создания швов, арматуры и крепежных элементов.
Таким образом, значение нерастяжимости нити в промышленности заключается в обеспечении стабильности и прочности материала, сохранении формы и размеров изделия, а также в создании надежных соединений и компонентов. Это свойство играет важную роль в различных отраслях и способствует повышению качества и надежности производимых изделий.
Нить, будучи невесомой и нерастяжимой, обладает рядом значимых свойств и применений.
Во-первых, невесомость нити означает, что она может быть использована для создания легких и деликатных конструкций. Например, нить может служить основой для вышивки, создания воздушных штор или вязания тонкой одежды. Благодаря своей невесомости, нить с легкостью принимает форму и позволяет создавать эстетически привлекательные изделия.
Во-вторых, нерастяжимость нити имеет важное значение для его применения в различных сферах. Нить, не поддаваясь растяжению, является надежным материалом для шитья и вязания, поскольку удерживает свою форму и не теряет прочность со временем. Кроме того, нерастяжимая нить может использоваться в медицинских процедурах, где требуется выдерживать натяжение и не допускать отклонений
Кроме того, нерастяжимая нить может использоваться в медицинских процедурах, где требуется выдерживать натяжение и не допускать отклонений.
Таким образом, невесомость и нерастяжимость нити способствуют ее широкому применению в различных областях, от ремесел и дизайна до медицины и строительства. Эти свойства делают нить универсальным и важным материалом, способным создавать красоту, облегчать процессы и обеспечивать надежность.
Современная теория механизмов
Существует понятие «типовые механизмы», которое объединяет ряд простых механизмов, имеющих при различном функциональном назначении применение в разнопрофильных машинах. К ним относятся простейшие механизмы:
- рычажные;
- зубчатые;
- планетарные;
- кулачковые;
- манипуляционные и т.п.
Рациональное проектирование машин определяется вариантами используемых в их составе простых механизмов и систем механизмов, благодаря которым изыскиваются оптимальные технические решения.
Существует две системы классификации простых механизмов: по назначению и конструкции. На практике их применение часто основывается на взаимно сочетающихся характеристиках.
Теория механизмов предполагает опираться на те свойства простых механизмов, которые являются общими, независимо от конкретного целевого назначения аппарата. К примеру, механизм в виде зубчатого колеса, создающий вращательное движение, используется как в часах, так и в автомобиле, промышленных станках и т.д.
Насколько эффективной будет работа создаваемой машины, зависит от правильности выбора механизмов. Выбор происходит в пользу тех, у которых выше производительность, надежность, точность. Также акцент делается на экономичность и доступность сырья для изготовления.
Применение механизмов началось в древности. Первыми из них были ловушки для зверей, которые удовлетворяли основной инстинкт человека — борьбу с голодом.
Сегодня для современной техники большое значение имеют:
- Механизмы манипуляторов (устройств, предназначенных для воспроизведения движений руки человека). Благодаря таким устройствам создаются промышленные роботы, которые приходят на помощь в самых сложных условиях и быстро выполняют утомительные работы, часто во вредных условиях.
- Самонастраивающиеся механизмы. Особенностью конструкции является способность изменять автоматически свое движение, создавая оптимальные условия для общей работы прибора.
- Механизмы медицинских аппаратов. Они воспроизводят физиологические процессы в теле человека. Примеры: искусственные легкие, искусственная почка, стимулятор сердца и т.п. Благодаря использованию таких приборов удается сохранить человеку жизнь даже в критических ситуациях.
Еще недавно в создании технических приборов использовались только простые механизмы, которые имели одну либо две степени подвижности. Сегодня их в одном приборе заключается много, что стало приемлемым благодаря использованию высокотехнологичных систем управления. Они в состоянии обеспечить эффективное функционирование аппаратов целиком или их отдельных частей.
Сверхтонкая нить: невесомость и износостойкость
Созданная человеком, сверхтонкая нить становится одним из самых удивительных материалов в мире. Ее уникальные свойства вызывают удивление и интерес у ученых и инженеров.
Главной характеристикой сверхтонкой нити является ее невесомость. Благодаря этому свойству, она может быть использована в различных областях, где требуется легкость и маневренность. Например, в космической промышленности сверхтонкая нить используется для создания космических тросов и антенн, которые должны быть легкими и прочными одновременно.
Несмотря на свою невесомость, сверхтонкая нить также обладает высокой износостойкостью. Она способна выдерживать огромные нагрузки и сохранять свою прочность даже при повреждении. Это делает ее незаменимым материалом в производстве спортивных снарядов, парашютов и защитного снаряжения.
Сверхтонкая нить также используется в медицинской сфере. Ее невесомость и износостойкость позволяют использовать ее для создания швов после операций и ран. Благодаря этому свойству, нить не натирает кожу и не вызывает раздражений, ускоряя процесс заживления.
Исследования и разработки в области сверхтонкой нити продолжаются, и это открывает новые возможности для ее использования. В будущем, мы можем увидеть еще больше уникальных применений этого материала и его свойств.
Силы упругости: пружины, канаты и нити
В задачах в этой статьи рассмотрены случаи, когда тело поднимают или опускают с ускорением. При этом натяжение нити, на которой подвешен груз, разное. Даны примеры составления уравнений по второму закону Ньютона в проекциях на оси.
Задача 1. Грузовик взял на буксир легковой автомобиль массой т и, двигаясь равноускоренно, за с проехал м. На сколько при этом удлиняется трос, соединяющий автомобили, если его жесткость Н/м? Трение не учитывать.
Удлинение троса можно найти, зная силу упругости:
Так как трение учитывать не нужно, то по второму закону Ньютона
Следовательно,
Определим ускорение грузовика:
Окончательно для удлинения троса получаем:
Ответ получен в метрах, можно записать его в мм: 0,64 мм.
Задача 2. На нити, выдерживающей натяжение Н, поднимают груз массой кг из состояния покоя вертикально вверх. Считая движение равноускоренным, найти предельную высоту , на которую можно поднять груз за с так, чтобы нить не оборвалась.
Запишем второй закон Ньютона в проекция на вертикальную ось:
Тогда ускорение равно:
Высота, на которую тело можно поднять с таким ускорением, равна
Ответ: 5 м
Задача 3. Веревка выдерживает груз массой кг при вертикальном подъеме его с некоторым ускорением и груз массой кг при опускании его с таким же по модулю ускорением. Какова максимальная масса груза , который можно поднимать или опускать на этой веревке с постоянной скоростью?

Запишем уравнения по второму закону как для подъема, так и для спуска тела. Направим ось вверх, тогда при подъеме:
При спуске:
Ускорение по условию одно и то же, тогда:
Приравняв, можем найти силу натяжения веревки, которую она выдерживает:
Если бы груз массой просто висел на такой веревке, то мы бы записали
Следовательно,
Ответ: 190 кг
Задача 4. Груз массой кг подвешен к пружине жесткостью Н/м. Длина пружины в нерастянутом состоянии м. Найти длину пружины , когда на ней висит груз. Какой будет длина пружины, если пружина с грузом будет находиться в лифте, движущемся с ускорением м/с, направленным а) вверх; б) вниз?
Если груз повешен на пружину, ее длина увеличивается:
При движении лифта вверх запишем второй закон (ось направлена вверх):
При движении лифта вниз запишем второй закон (ось направлена вверх):
Тогда длина пружины в этом случае:
Ответ: , , .
Задача 5. Четырьмя натянутыми нитями груз закреплен на тележке. Силы натяжения горизонтальных нитей соответственно и , а вертикальных – и . С каким ускорением движется тележка по горизонтальной плоскости?
Запишем уравнения по второму закону в проекциях на оси, которые расположим традиционно: ось вправо, ось – вверх. Тогда, если тележка движется вправо, по оси, имеем:
Из второго уравнения найдем массу груза:
Если же тележка движется влево (против оси), то изменится только первое уравнение:
Тогда ускорение тележки (и груза) равно:
easy-physic.ru
Самые популярные законы физики, которые могут встретиться в задаче
Самый большой раздел, представленный в кодификаторе, — механика. Задачи на темы именно из этого раздела встречаются в задании 26. Приведем некоторые из законов с указанием функции для обоснования.
| Законы Ньютона | Материальная точка | Размеры тел не существенны в решении |
| Инерциальная система отсчёта | Можно пренебречь влиянием вращения Земли | |
| Движение связанных тел | Невесомая нить | — Массой нити можно пренебречь по сравнению с массой связанных ею тел — Силы натяжения одинаковы во всех точках нити |
| Нерастяжимая нить | Деформацией нити в условиях данной задачи можно пренебречь | |
| Идеальный блок | Массой блока и силой трения в условиях данной задачи можно пренебречь | |
| Закон Гука | Тело восстанавливает свою форму после снятия деформирующей силы |
Как определить силу, формулы
Натяжение проявляется по-разному. Поэтому сила натяжения может рассчитываться определенным образом, в зависимости от окружающих условий.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут
С неподвижно закрепленным верхним концом
Простейшим примером проявления силы натяжения является нить с закрепленным на ней грузом. Верхний конец такого подвеса фиксируется неподвижно. В этом случае сила натяжения будет соответствовать силе тяжести, которая действует на тело. Формула для расчета:
\(F=F_{тяж}=m*g\)
где m – это масса тела, а g представляет собой ускорение свободного падения.
Если нить под углом
В случае, когда груз расположен под определенным углом, характер силы натяжения несколько изменяется. Примером такой системы выступает маятник.
\(F_n=m*g*cos(a)\)
где а равен углу отклонения.
Формула с учетом ускорения и массы
В ситуации, при которой на груз оказывается сила натяжения, приводящая его в движение вверх, следует использовать такую формулу для ее расчета:
\(F=F_{тяж}+m*a\)
Понятие нерастяжимости в волокнах и тканях
Нерастяжимость волокон и тканей является важным свойством, которое определяет их поведение и применение в различных отраслях промышленности. Нити, обладающие высокой степенью нерастяжимости, имеют ряд преимуществ по сравнению с растяжимыми материалами.
Причины, по которым нить может быть нерастяжимой, связаны с её структурой и составом. Волокна, из которых состоит нить, могут быть сплетены или скручены вместе. Эти структуры обеспечивают нитью высокую прочность и нерастяжимость. Для достижения нерастяжимости нити могут быть добавлены различные модификаторы, такие как арамидные волокна или металлические нити.
Свойства нерастяжимых нитей и тканей определяют их широкое применение в различных областях. В медицине они могут использоваться для создания швов при проведении хирургических операций или в кардиологических имплантах. В авиации и автомобилестроении нерастяжимые материалы применяются для создания ремней безопасности и проводных тросов, обеспечивая высокую надежность и безопасность объектов.
Также стоит отметить, что нерастяжимость нитей и тканей имеет важное значение при создании специальной одежды, такой как скафандры, защитные костюмы, подводные костюмы и другие. Нерастяжимый материал обеспечивает защиту от повреждений и сохраняет свои формальные свойства при экстремальных нагрузках
Итак, нерастяжимость в волокнах и тканях является важным свойством, обеспечивающим прочность, надежность и защитные свойства материалов. Она позволяет использовать такие материалы в широком спектре областей, где требуется высокая степень нерастяжимости и прочности.
Тончайшая материя: нерастяжимая и твердая
Тончайшая нить не поддается растяжению даже при больших нагрузках. Это свойство обусловлено особым строением и взаимодействием молекул, из которых состоит нить. Молекулы нити расположены таким образом, что они плотно сцеплены друг с другом, образуя прочную структуру. Благодаря этому, нить не растягивается и выдерживает значительные нагрузки.
Кроме того, нить также является твердой материей. Твердость нити, подобно нерастяжимости, обусловлена особыми свойствами молекул. Межмолекулярные силы притяжения придают нити твердость и жесткость. Благодаря этому, нить легко удерживает форму и не деформируется при действии нагрузок.



























