Нормированное векторное пространство

В нормированное векторное пространство V, одно из определяющих свойств норма это неравенство треугольника:
- ‖Икс+у‖≤‖Икс‖+‖у‖∀Икс,у∈V{ displaystyle displaystyle | x + y | leq | x | + | y | quad forall , x, y in V}
то есть норма не больше суммы норм двух векторов. Это также называется субаддитивность. Чтобы любая предлагаемая функция вела себя как норма, она должна удовлетворять этому требованию.
Если нормированное пространство евклидов, или, в более общем смысле, строго выпуклый, тогда ‖Икс+у‖=‖Икс‖+‖у‖{ Displaystyle | х + у | = | х | + | у |} если и только если треугольник, образованный Икс, у, и Икс + у, является вырожденным, то естьИкс и у находятся на одном луче, т.е. Икс = 0 или у = 0, илиИкс = α y для некоторых α > 0. Это свойство характеризует строго выпуклые нормированные пространства, такие как ℓп пространства с 1 < п < ∞. Однако есть нормированные пространства, в которых это неверно. Например, рассмотрим самолет с ℓ1 норма ( Манхэттенское расстояние ) и обозначить Икс = (1, 0) и у = (0, 1). Тогда треугольник, образованныйИкс, у, и Икс + у, невырожден, но
- ‖Икс+у‖=‖(1,1)‖=|1|+|1|=2=‖Икс‖+‖у‖.{ Displaystyle | х + у | = | (1,1) | = | 1 | + | 1 | = 2 = | х | + | у |.}
Примеры норм
Абсолютное значение как норма для реальная линия. Чтобы быть нормой, неравенство треугольника требует, чтобы абсолютная величина удовлетворять для любых реальных чисел Икс и у:
-
- |Икс+у|≤|Икс|+|у|,{ Displaystyle | х + у | Leq | х | + | у |,}
- что он делает.
Доказательство:
- −|Икс|≤Икс≤|Икс|{ displaystyle — left vert x right vert leq x leq left vert x right vert}
- −|у|≤у≤|у|{ displaystyle — left vert y right vert leq y leq left vert y right vert}
После добавления
- −(|Икс|+|у|)≤Икс+у≤|Икс|+|у|{ Displaystyle — ( влево верт х вправо верт + влево верт у вправо верт) Leq х + у Leq влево верт х вправо верт + влево верт у вправо vert}
Используйте тот факт, что |б|≤а⇔−а≤б≤а{ displaystyle left vert b right vert leq a Leftrightarrow -a leq b leq a}(с участием б заменяется Икс+у и а от |Икс|+|у|{ displaystyle left vert x right vert + left vert y right vert}), у нас есть
- |Икс+у|≤|Икс|+|у|{ Displaystyle | х + у | Leq | х | + | у |}
Неравенство треугольника полезно в математический анализ для определения наилучшей верхней оценки размера суммы двух чисел в терминах размеров отдельных чисел.
Существует также более низкая оценка, которую можно найти с помощью обратное неравенство треугольника в котором говорится, что для любых действительных чисел Икс и у:
- |Икс−у|≥||Икс|−|у||.{ displaystyle | x-y | geq { bigg |} | x | — | y | { bigg |}.}
Внутренний продукт как норма в внутреннее пространство продукта. Если норма возникает из внутреннего произведения (как в случае евклидовых пространств), то неравенство треугольника следует из Неравенство Коши – Шварца следующим образом: данные векторы Икс{ displaystyle x} и у{ displaystyle y}, и обозначив внутренний продукт как ⟨Икс,у⟩{ Displaystyle langle х, у rangle}:
-
‖Икс+у‖2{ Displaystyle | х + у | ^ {2}} =⟨Икс+у,Икс+у⟩{ displaystyle = langle x + y, x + y rangle} =‖Икс‖2+⟨Икс,у⟩+⟨у,Икс⟩+‖у‖2{ displaystyle = | x | ^ {2} + langle x, y rangle + langle y, x rangle + | y | ^ {2}} ≤‖Икс‖2+2|⟨Икс,у⟩|+‖у‖2{ Displaystyle Leq | х | ^ {2} +2 | langle x, y rangle | + | y | ^ {2}} ≤‖Икс‖2+2‖Икс‖‖у‖+‖у‖2{ Displaystyle Leq | х | ^ {2} +2 | х | | у | + | у | ^ {2}} (по неравенству Коши – Шварца) =(‖Икс‖+‖у‖)2{ Displaystyle = влево ( | х | + | у | вправо) ^ {2}}.
Неравенство Коши – Шварца превращается в равенство тогда и только тогда, когда Икс и улинейно зависимы. Неравенство⟨Икс,у⟩+⟨у,Икс⟩≤2|⟨Икс,у⟩|{ displaystyle langle x, y rangle + langle y, x rangle leq 2 | langle x, y rangle |}превращается в равенство для линейно зависимых Икс{ displaystyle x} и у{ displaystyle y}тогда и только тогда, когда один из векторов Икс или у это неотрицательный скаляр другого.
- Извлечение квадратного корня из окончательного результата дает неравенство треугольника.
п-норма: обычно используемой нормой является п-норма:
-
- ‖Икс‖п=(∑я=1п|Икся|п)1п ,{ Displaystyle | х | _ {p} = left ( sum _ {i = 1} ^ {n} | x_ {i} | ^ {p} right) ^ {1 / p} ,}
- где Икся компоненты вектора Икс. Для п = 2 то п-норма становится Евклидова норма:
- ‖Икс‖2=(∑я=1п|Икся|2)12=(∑я=1пИкся2)12 ,{ Displaystyle | х | _ {2} = влево ( сумма _ {я = 1} ^ {п} | х_ {я} | ^ {2} вправо) ^ {1/2} = влево ( sum _ {i = 1} ^ {n} x_ {i} ^ {2} right) ^ {1/2} ,}
- который Теорема Пифагора в п-размеры, очень частный случай, соответствующий внутренней норме продукта. Кроме случая п = 2, то п-норма не внутренняя норма продукта, потому что она не удовлетворяет закон параллелограмма. Неравенство треугольника для общих значений п называется Неравенство Минковского. Он принимает вид:
- ‖Икс+у‖п≤‖Икс‖п+‖у‖п .{ displaystyle | x + y | _ {p} leq | x | _ {p} + | y | _ {p} .}
Please enable JavaScript.
Coggle requires JavaScript to display documents.
Треугольник — геометрическая фигура, образованная тремя отрезками, которые…
- Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой
- Виды треугольников
- По углам
Признаки равенства прямоугольных треугольников
По двум катетам
По катету и острому углу
По гипотенузе и острому углу
По гипотенузе и катету
Свойства:
Сумма острых углов прямоугольного треугольника равна 90˚.
Катет, противолежащий углу в 30˚, равен половине гипотенузы.
Теорема Пифагора квадрат гипотенузы равен сумме квадратов катетов.
Центр описанной окружности – есть середина гипотенузы.
Радиус R описанной окружности есть половина гипотенузы
Медиана, проведенная к гипотенузе, равна ее половине
Тригонометрические свойства
Синусом угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.
Косинусом угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.
Тангенсом угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.
Котангенсом угла в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему.
По сторонам
Углы равнобедренного треугольника, прилежащие к основанию, равны.
Биссектриса, медиана и высота, проведенные к основанию, совпадают.
Биссектриса, медиана и высота, проведенные из одной вершины, совпадают.
Равносторонний треугольник имеет центр — точка пересечения биссектрис, медиан, высот, центр описанной и вписанной окружностей.
Равные треугольники: Треугольники называют равными, если у них соответствующие стороны и углы равны
1 признак: По двум сторонам и углу между ними
2 признак: По стороне и двум прилежащим к ней углам
3 признак: По трем сторонам
Подобные треугольники — треугольники, углы у которых соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника
1 признак: по двум пропорциональным сторонам и углу между ними
2 признак:по двум углам
3 признак: по трем пропорциональным сторонам
Замечательные линии треугольника
Биссектриса — это отрезок биссектрисы угла треугольника, проведенной из данной вершины, соединяющий эту вершину с точкой на противолежащей стороне.
Все три биссектрисы треугольника пересекаются в одной точке.
Точка пересечения биссектрис треугольника является центром вписанной в треугольник окружности.
Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные двум другим сторонам:
Высота — перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противолежащую сторону.
Все три высоты треугольника пересекаются в одной точке. Эта точка называется ортоцентром треугольника.
Если AH и BM — прямые, содержащие высоты AH и BM треугольника ABC, то треугольники CHM и CAB подобны, коэффициент подобия равен модулю косинуса угла C.
Медиана- это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Все медианы треугольника пересекаются в одной точке, называемой центроидом (центром тяжести) треугольника
В точке пересечения медианы треугольника делятся в отношении два к одному, считая от вершины: AO:OA1=BO:OB1=CO:OC1=2:1
Теорема косинусов квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Теорема синусов стороны треугольника пропорциональны синусам противолежащих углов.
Площадь треугольника
Формула Герона
Средняя линия треугольника- это отрезок, соединяющий середины двух его сторон.
Определить существование треугольника по трем сторонам
С клавиатуры вводятся длины трех отрезков. Определить, можно ли из них составить треугольник.Решение задачи на языке программирования Python
У треугольника сумма любых двух сторон должна быть больше третьей. Иначе две стороны просто «лягут» на третью и треугольника не получится.
Пользователь вводит длины трех сторон. Программа должна определять, может ли существовать треугольник при таких длинах. Это значит, необходимо сравнить суммы всех пар сторон с оставшейся третьей стороной. Чтобы треугольник существовал, сумма всегда должна быть больше отдельной стороны или, по крайней мере, не меньше, если учитывать так называемый вырожденный треугольник.
Поскольку всего три стороны, то можно составить три варианта сложения двух сторон: a + b, b + c, a + c. Первую сумму сравниваем с оставшейся стороной c, вторую — с a и третью — с b. Если хотя бы в одном случае сумма окажется не больше третьей стороны, то делается вывод, что треугольник не существует.
print("Стороны:")
a = float(input("a = "))
b = float(input("b = "))
c = float(input("c = "))
if a + b > c and a + c > b and b + c > a:
print("Треугольник существует")
else:
print("Треугольник не существует")
Можно решить задачу сложнее. Если требуется также определить, какая из сторон больше суммы двух других, то решение может быть таким:
print("Длины сторон треугольника:")
a = float(input("a = "))
b = float(input("b = "))
c = float(input("c = "))
flag = ''
if a + b > c:
if a + c > b:
if b + c > a:
print("Треугольник есть")
else:
flag = 'a'
else:
flag = 'b'
else:
flag = 'c'
if flag != '':
print("Треугольника нет")
print("'%s' > суммы других" % flag)
Особого смысла использовать переменную flag здесь нет. Она просто позволяет лишний раз не писать в программе строки, информирующие о том, что треугольник не существует.
Пример выполнения программы:
Длины сторон треугольника: a = 4 b = 5 c = 10 Треугольника нет 'c' > суммы других
Более изящным решением является использование оператора множественного ветвления языка программирования Python: if-elif-else.
print("Длины сторон треугольника:")
a = float(input("a = "))
b = float(input("b = "))
c = float(input("c = "))
flag = ''
if a + b <= c:
flag = 'c'
elif a + c <= b:
flag = 'b'
elif b + c <= a:
flag = 'a'
else:
print("Треугольник есть")
if flag != '':
print("Треугольника нет")
print("'%s' > суммы других" % flag)
Здесь сравнение происходит от обратного: утверждается, что сумма двух сторон меньше или равна третьей. Если это так (утверждение верно), то треугольника не существует. «Слишком длинная сторона» определяется в зависимости от того, в заголовке какой ветки логическое выражение возвращает истину.
Больше задач в PDF
[править] Свойства и особенности треугольников
Трём точкам пространства, не лежащим на одной прямой (и образуемому ими невырожденному треугольнику), обязательно соответствует одна и только одна плоскость. Это весьма уникально — так как меньшему количеству точек соответствуют прямая и точка, а уже четыре точки могут находится вне единой плоскости.
Треугольник — это часть плоскости, ограниченная минимально возможным количеством сторон. Любой многоугольник можно точно разбить на треугольники, лишь связав его вершины отрезками, не пересекающими его стороны. С некоторым приближением, на треугольники можно разбить поверхность любой формы, как на плоскости так и в пространстве. Процесс разбиения на треугольники называется триангуляция.
Существует раздел математики, целиком посвящённый изучению закономерностей треугольников — Тригонометрия.
Треугольник, когда не вырожден — всегда выпуклый многоугольник.
Для треугольника всегда существует одна вписанная и одна описанная окружность.
Трапеция
Трапеция — это четырехугольник, у которого две стороны параллельны, а две не параллельны.
Основное свойство: в трапецию можно вписать окружность, если сумма ее оснований равна сумме боковых сторон.
Как найти площадь трапеции:
S = (a + b) : 2 × h, где a, b — два разных основания, h — высота трапеции.

Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны и был расположен перпендикулярно к этим основаниям.
Формула периметра для равнобедренной трапеции отличается от прямоугольника тем, что у равнобедренной трапеции есть две равные стороны.
P = a + b + 2 × c, где a, b — параллельные стороны, c — две длины одинаковых сторон.
Что такое треугольник
Рассмотрим понятие треугольника. Пусть на плоскости дана трехзвенная замкнутая ломаная. Тогда эта ломаная разделяет множество оставшихся точек плоскости на ограниченную и неограниченную фигуры. При этом ограниченная фигура называется частью плоскости, ограниченной данной ломаной. Например, на рисунке 59, а изображена часть плоскости, ограниченная трехзвенной замкнутой ломаной ABC.
Определение. Треугольником называется геометрическая фигура, состоящая из трехзвенной замкнутой ломаной и части плоскости, ограниченной этой ломаной.
Вершины ломаной называются вершинами треугольника, а звенья ломаной — сторонами треугольника.
Точки треугольника, не принадлежащие его сторонам, называются внутренними.
Треугольник, вершинами которого являются точки А, В и С, обозначается следующим образом:
АВС
BСА
CАВ
На рисунке 59, а изображен треугольник ABC. Точки А, В и С — вершины этого треугольника, а отрезки AB, ВС и АС — его стороны. На рисунке 59, B показан треугольник AFD, содержащийся в грани куба.
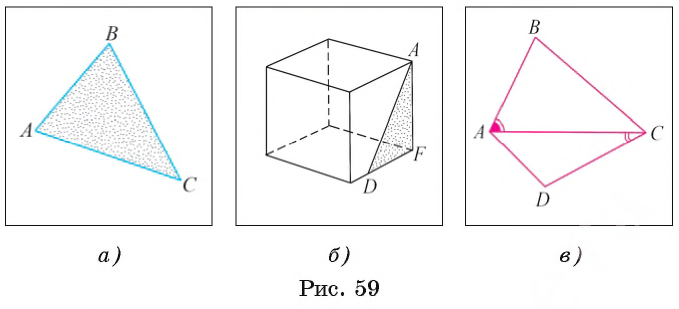
Углы АBС, АСВ и САВ (см. рис. 59, а) называются внутренними углами треугольника ABC или просто углами треугольника. Иногда они обозначаются одной буквой:
A,
B,
CСтороны и углы треугольника называются его элементами.
На рисунке 59, в изображены треугольники ABC и ACD, у которых общая сторона АС. Угол ВАС — внутренний угол треугольника ВАС,
ACD
Периметром треугольника называется сумма длин всех его сторон. Периметр треугольника ABC обозначается PABC.
Конструкции, имеющие треугольную форму, применяются при строительстве архитектурных сооружений, мостов и жилых зданий. Например, при постройке крыш некоторых домов используются стропила, имеющие форму треугольников (рис. 60, а).
Для треугольников, как и любых геометрических фигур, определяется понятие их равенства.
Два треугольника называются равными, если их можно совместить наложением, т. е. можно совместить их вершины, стороны и углы.
Рассмотрим пример. Если лист бумаги, имеющий форму прямоугольника, разрезать на две части, как показано на рисунке 60, б, то мы получим модели равных треугольников. Непосредственно можно убедиться, что полученные части можно наложить одна на другую так, что они совместятся.
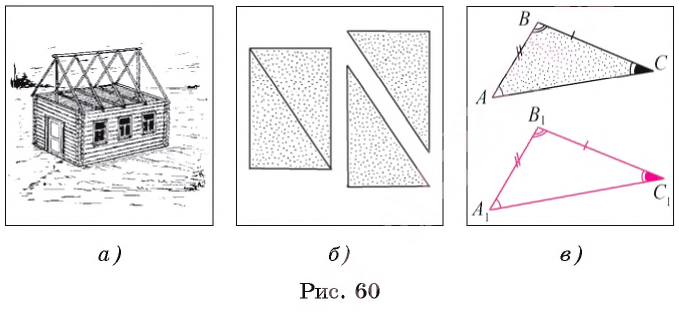
Два равных треугольника ABC и A1B1C1(рис. 60, в) можно совместить так, что попарно совместятся их вершины, стороны и углы. Другими словами, если два треугольника равны, то стороны и углы одного треугольника соответственно равны сторонам и углам другого треугольника. Подчеркнем, что:
- в равных треугольниках против соответственно равных сторон лежат равные углы;
- в равных треугольниках против соответственно равных углов лежат равные стороны.
Например, в равных треугольниках ABC и A1B1C1, изображенных на рисунке 60, в, против равных сторон ВС и В1С1лежат равные углы А и А1. Против равных углов С и С1 лежат равные стороны AB и A1B1.
Если треугольники ABC и A1B1C1 равны, то это обозначается следующим образом:
ABC
A1B1C1
Заметим, что для установления равенства треугольников необязательно их совмещать один с другим, а достаточно сравнить некоторые их элементы (стороны и углы).
Для доказательства равенства треугольников пользуются соответствующими теоремами (признаками), которые позволяют на основании равенства некоторых элементов треугольников делать вывод о равенстве самих треугольников.
Топ вопросов за вчера в категории образование
Образование 06.09.2023 11:36 3128 Петрина Макс.
Как пишется: «средне-техническое» или «средне техническое » образование?
Ответов: 1
Образование 26.08.2023 14:06 3400 Пинчук Никита.
Какие фрукты начинаются на букву «Р»?
Ответов: 1
Образование 02.09.2023 05:24 2337 Салымгереев Акылбек.
Как правильно: по получении или по получению?
Ответов: 1
Образование 20.08.2023 17:20 1960 Плотникова Юля.
Как правильно: «не подходит» или «неподходит»?
Ответов: 1
Образование 10.10.2023 17:31 1886 Швецов Степан.
Какое проверочное слово к слову иссЯкать?
Ответов: 1
Образование 24.10.2023 18:21 70 Вондок Ли.
Как правильно Ярославич ли Ярославович?
Ответов: 1
Образование 09.09.2023 09:10 3123 Дианочка Диана.
Какие фрукты начинаются на букву «Ф»?
Ответов: 1
Образование 16.09.2023 23:41 3242 Ткачёв Витя.
Какое проверочное слово к слову ОГОРОД?
Ответов: 1
Образование 26.09.2023 09:48 2562 Сапроненков Евгений.
Какое проверочное слово к слову «облегчить» (облегчение)?
Ответов: 1
Образование 28.10.2023 10:34 3200 Угланова Яна.
Как решить: Для перевозки груза потребовалось 24 машины грузоподъём. 7,5 т?
Ответов: 1
Примеры задач
Публикации по теме:
- Нахождение площади квадрата: формула и примеры
- Нахождение площади прямоугольника: формула и пример
- Нахождение площади треугольника: формула и примеры
- Нахождение площади круга: формула и примеры
- Нахождение площади трапеции: формула и примеры
- Нахождение площади параллелограмма: формула и примеры
- Нахождение площади эллипса: формула и пример
- Нахождение площади выпуклого четырехугольника: формула и пример
- Нахождение периметра квадрата: формула и задачи
- Нахождение периметра треугольника: формула и задачи
- Нахождение периметра ромба: формула и задачи
- Нахождение периметра трапеции: формула и задачи
- Нахождение периметра параллелограмма: формула и задачи
- Нахождение длины окружности: формула и задачи
- Теорема Пифагора для прямоугольного треугольника: формула и задачи
- Теорема косинусов для треугольника: формула и задачи
- Теорема синусов для треугольника: формула и задачи
- Тригонометрические функции острого угла в прямоугольном треугольнике
- Нахождение объема конуса: формула и задачи
- Нахождение объема цилиндра: формула и задачи
- Нахождение объема шара: формула и задачи
- Нахождение объема пирамиды: формула и задачи
- Нахождение площади правильного шестиугольника: формула и примеры
- Нахождение объема тетраэдра: формула и задачи
- Нахождение объема призмы: формула и задачи
- Нахождение объема параллелепипеда: формула и задачи
- Нахождение площади поверхности куба: формула и задачи
- Нахождение площади поверхности цилиндра: формула и задачи
- Нахождение площади поверхности конуса: формула и задачи
- Нахождение площади поверхности шара (сферы): формула и задачи
- Нахождение площади поверхности вписанного в цилиндр шара
- Нахождение радиуса шара: формула и примеры
- Нахождение радиуса круга: формула и примеры
- Нахождение радиуса цилиндра: формула и примеры
- Нахождение площади прямоугольного параллелепипеда: формула и пример
- Нахождение площади правильной призмы: формула и задачи
- Нахождение площади правильной пирамиды: формулы
- Теорема Менелая: формулировка и пример с решением
- Теорема о внешнем угле треугольника: формулировка и задачи
- Теорема Чевы: формулировка и пример с решением
- Теорема Стюарта: формулировка и пример с решением
- Теорема о трех перпендикулярах
- Признаки равенства треугольников
- Признаки подобия треугольников
- Признаки равенства прямоугольных треугольников
- Свойства прямоугольного треугольника
- Свойства равнобедренного треугольника: теория и задача
- Свойства равностороннего треугольника: теория и пример задачи
- Определение и свойства медианы треугольника
- Определение и свойства медианы прямоугольного треугольника
Треугольник. Равенство треугольников
Треугольник — фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки. Точки называются вершинами, а отрезки — сторонами.
Треугoльник — жесткая фигура. Это свойство используют при строительстве мостовых арок, конструировании подъемных кранов и т.д. Свойства треугольника системно изложены в «Началах» Эвклида. Знак для обозначения треугольника еще в I в. н.э. применил древнегреческий учений Герон, а знак Δ применяется с IV в. н.э.
Медиана, биссектриса и высота треугольника
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Медиана делит стороны пополам. Три медианы треугольника пересекаются в одной точке и в этой точке делятся в отношении 2:1, считая от вершины.
Биссектриса треугольника делит угол пополам. Биссектриса угла треугольника делит противоположную сторону в отношении длин прилежащих сторон. Три биссектрисы пересекаются в одной точке, которая является центром окружности, вписанной в треугольник.
Высотой треугольника называется отрезок, опущенный из вершины треугольника на противоположную сторону. В тупоугольном треугольнике высота опускается на продолжение стороны. Три высоты треугольника всегда пересекаются в одной точке. В случае тупого угла в одной точке пересекаются продолжения высот.
Равные треугольники
Два треугольника называются равными, если их можно совместить наложением.
Аксиома существования треугольника, равного данному.
Каким бы ни был треугольник, существует треугольник, равный ему в заданном расположении относительно данной полупрямой.
Свойства равных треугольников
1. В равных треугольниках соответствующие стороны равны.
2. В равных треугольниках соответствующие углы равны.
3. Периметры равных треугольников равны.
4. Площади равных треугольников равны.
5. Против равных сторон лежат равные углы.
6. Против равных углов лежат равные стороны.
Признаки равенства треугольников
Признаки равенства треугольников — одна из основных теорем геометрии. Треугольник на евклидовой плоскости однозначно можно определить по следующим тройкам основных элементов:
- Первый признак — по двум сторонам и углу между ними.
- Второй признак – по двум углам и прилежащей стороне.
- Третий признак – по трём сторонам.
Дополнительные признаки равенства
• Если две стороны и медиана, проведенная к третьей стороне треугольника, соответственно равны двум сторонам и медиане, проведенной к третьей стороне другого треугольника, такие треугольники равны.
• Если два угла и высота,проведенная к стороне, к которой прилегают эти углы, одного треугольника, соответственно равны двум углам и высоте, проведенной к стороне, к которой прилегают эти углы, другого треугольника, то такие треугольники равны.
• Если сторона, высота и медиана, проведенные к стороне одного треугольника, соответственно равны стороне, высоте и медиане, проведенным к этой стороне другого треугольника, то эти треугольники равны.
• Если медиана и углы, на которые она делит угол, одного треугольника, соответственно равны медиане и углам,на которые она делит угол, другого треугольника, эти треугольники равны.
Это конспект по геометрии на тему «Треугoльник. Равенство треугольников». Выберите дальнейшие действия:
- Перейти к следующему конспекту: ЗАДАЧИ на Признаки равенства треугольников
- Вернуться к Списку конспектов по геометрии
Свойства
Определение невырожденного треугольника в геометрии основано на том, что углы треугольника суммируются в 180 градусов, каждая сторона больше нуля, и сумма двух сторон всегда больше третьей стороны. Любая грань треугольника является отрезком, соединяющим две его вершины.
Примерами невырожденных треугольников могут служить треугольник со сторонами 3, 4 и 5, а также треугольник с углами 30, 60 и 90 градусов.
Равенство суммы углов треугольника 180 градусам.
Стандартное определение треугольника в геометрии — это фигура, образованная тремя сторонами и тремя вершинами. Каждая сторона соединяет две вершины, а каждый угол образуется двумя сторонами, исходящими из одной вершины. Углы треугольника также могут быть классифицированы как острые (меньше 90 градусов), прямые (равные 90 градусам) или тупые (больше 90 градусов).
Признак невырожденного треугольника — это условие, при котором сумма длин любых двух сторон треугольника всегда больше длины третьей стороны. Иначе говоря, треугольник должен быть «закрытой» фигурой, а не прямой линией или точкой.
Важным свойством невырожденного треугольника является равенство суммы углов треугольника 180 градусам. Это значит, что сумма всех внутренних углов треугольника равна 180 градусам. Например, если у нас есть треугольник с углами 60 градусов, 70 градусов и 50 градусов, то их сумма будет равна 180 градусам.
Сумма длин двух сторон треугольника всегда больше длины третьей стороны.
В геометрии треугольник представляет собой плоскую фигуру, образованную тремя отрезками, называемыми сторонами треугольника. Каждая сторона треугольника является гранью этой фигуры, а точки их пересечения – вершинами. Сумма длин двух сторон определенного треугольника всегда больше длины третьей стороны и служит важным признаком для определения невырожденного треугольника.
Позвольте рассмотреть пример, чтобы увидеть это свойство в действии. Предположим, что у нас есть треугольник с сторонами длиной 5, 7 и 10 единиц. Чтобы проверить, выполняется ли свойство суммы длин двух сторон, необходимо сложить длины двух самых коротких сторон:
| Стороны треугольника | Сумма длин двух сторон |
|---|---|
| 5, 7, 10 | 5 + 7 = 12 |
Как видим, сумма длин двух сторон треугольника равна 12. Затем сравниваем эту сумму с длиной третьей стороны:
| Стороны треугольника | Сумма длин двух сторон | Длина третьей стороны |
|---|---|---|
| 5, 7, 10 | 12 | 10 |
Как можно заметить, сумма длин двух сторон (12) больше длины третьей стороны (10), что подтверждает наше утверждение о том, что сумма длин двух сторон треугольника всегда больше длины третьей стороны.
Сумма длин двух сторон треугольника является важным свойством, она влияет на множество других характеристик треугольника, таких как его площадь, углы и отношения между сторонами.
Высоты треугольника пересекаются в одной точке — ортоцентре.
Одним из важных свойств треугольника является то, что все высоты треугольника пересекаются в одной точке, которая называется ортоцентром. Именно ортоцентр является точкой пересечения трех высот треугольника.
Ортоцентр имеет много геометрических свойств и является ключевой точкой в задачах треугольника. Он лежит внутри или на границе треугольника, в зависимости от его типа и положения высот. Более того, ортоцентр может быть использован для определения других важных элементов треугольника, таких как окружность Эйлера и описанная окружность.
Одно из основных свойств ортоцентра заключается в том, что отрезки, соединяющие ортоцентр с вершинами треугольника, перпендикулярны соответствующим сторонам. Это означает, что углы между сторонами треугольника и этими отрезками равны 90 градусам.
Еще одним важным признаком ортоцентра является его связь с площадью треугольника. Для любого треугольника, площадь треугольника ABC равна произведению половины основания BC на высоту, проведенную из вершины A:
SABC = 0.5 * BC * HA, где SABC — площадь треугольника ABC, BC — основание треугольника, HA — высота, проведенная из вершины A.
Таким образом, ортоцентр треугольника имеет большое значение и определение его свойств позволяет углубить понимание треугольника в геометрии. Благодаря своей особенной природе, ортоцентр является важным элементом в решении задач и определении основных характеристик треугольника.
Остались вопросы?
Занимаетесь изучением математики или готовитесь к экзаменам? Найти ответы на многие вопросы по истории треугольников, их свойств и типов вы можете на сайте с видеоуроками http://interneturok.ru. Здесь собраны лекции по школьному курсу геометрии. Удобная система поиска на сайте поможет быстро найти и узнать, что такое вписанный треугольник, какими свойствами обладает равносторонний треугольник, теорема Пифагора и ее доказательство, первый, второй и третий признаки равенства треугольников и многое другое. Школьный курс геометрии разделен по классам. На портале вы найдете уроки за 7, 8, 9, 10 и 11 классы по геометрии. Видеоуроки четко структурированы по классам, темам и конкретным учебникам.
Ключевые нюансы
Существует две линии SWT и SFT одинаковой толщины, которые соединяют свободные концы одной прямой ST. В итоге образуется ломаная. Изогнутая SFT именуется внутренней ломаной, а вот SWT внешней. В качестве примера лучше всего рассмотреть фигуру, которая соответствует математической теореме, что внешняя изогнутая превышает внутреннюю.
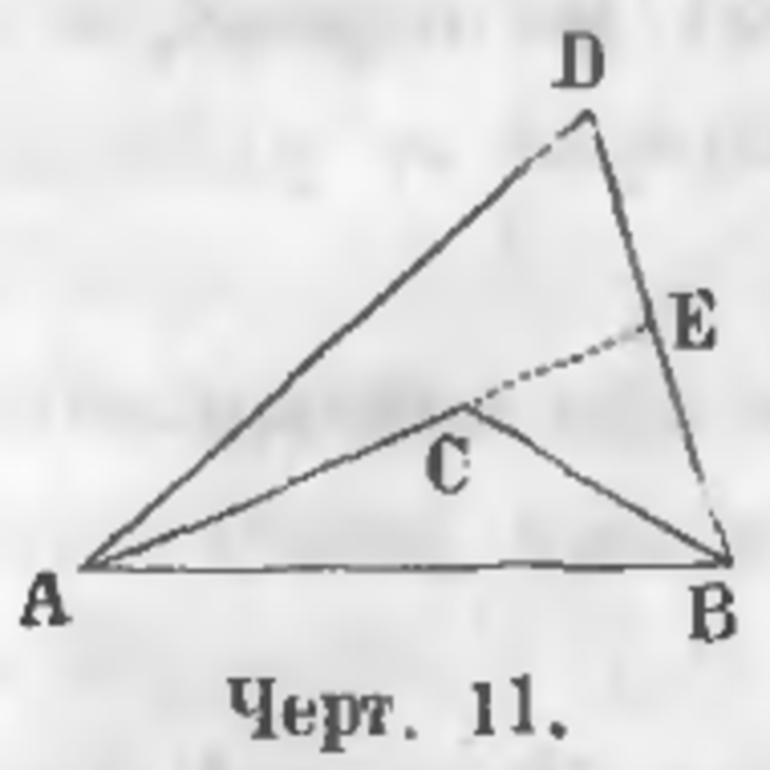
По условиям задачи были даны две ломаные: внутренняя SFT и внешняя SWT. Необходимо доказать, что SWT больше SFT. Для решения этой задачи нужно продолжить линию SF до пересечения с отрезком WT в точке Е. Линия SWE как ломаная гораздо больше прямой SE. Ломанная FET больше имеющейся прямой FT. Если сложить между собой все эти неравенства, то в итоге можно получить: SW+ WE + FE + ET > SF + FE + FT.
Для получения достоверного результата нужно вычесть из обеих частей неравенства по СЕ:
- SW+ WE + ET > SF + FT.
- WE + ET = WT.
Необходимо рассмотреть и вторую теорему, в соответствии с которой итоговая сумма пересекающихся изогнутых линий больше не пересекающихся. По условиям задачи были даны обычные пересекающиеся ломаные HLK и HRK, а также HR, LK и пересекающиеся части. Решение выглядит следующим образом: неравенства отрезков вытекают из того, что ломаная HEL гораздо больше прямой HL, а вот координаты KER превышают KR.
Нелишним также будет научиться находить общую меру сразу двух линий при помощи линейки. Это правило обязательно осваивают в начальных классах. Для поиска неизвестной общей меры обязательно нужно на большую линию наложить меньшую, потом первый остаток на меньший отрезок, а второй остаток на первый. Все эти манипуляции повторяют ровно до тех пор, пока самый последний остаток максимально не уложится в предпоследнем выполненном действии. Измерение линий всегда означает то, что учащемуся необходимо отыскать её отношение к другим отрезкам, принятым за единицу. Полученное значение называют длиной этой линии, которая может выражаться исключительно в каких-нибудь единицах.
Изучение ломаных линий очень важно, так как они окружают человека повсюду. Речь касается прямых линий, которые меняют своё первоначальное направление, замыкаются, а также пересекаются.
























